第2章 微分方程与动力系统
内容:@若冰(马世拓)
审稿:@陈思州
排版&校对:@何瑞杰
这一章我们主要介绍微分方程与一些动力系统模型。数学上对微分方程的研究是一项热点问题,在工程当中微分方程与动力系统也有着广泛的应用。我们除了会从高等数学与计算数值方法的角度分析微分方程的求解方法与底层逻辑,还会介绍在数学模型当中被广泛应用的微分方程模型。本章主要涉及到的知识点有:
- 微分方程的解法
- 如何用python解微分方程
- 偏微分方程及其求解方法
- 微分方程的基本案例
- 差分方程的求解
- 数值计算方法
- 元胞自动机
注意:本章的重点是理解微分方程在实际工程中的应用。如果对数学基础有疑问,可以参考相关的高等数学和数值分析教材。
2.1 微分方程的理论基础
微分方程是什么?如果你参加过高考,可能在高三备考中遇到过这样的问题:给定函数$f(x)$及其导数之间的等式,然后分析函数的性质,如单调性、零点等,但没有给出函数的解析式。这时你可能会想,如果能通过这个方程求出函数的通项形式该多好!微分方程的目的就是这样,它通过将函数$f$和它的若干阶导数联系起来形成一个方程(组),来求出函数的解析式或函数值随自变量变化的曲线。
2.1.1 函数、导数与微分
微分和导数其实是紧密相关的概念。我们通常将导数理解为函数在某一点处切线的斜率。而微分则描述的是当我们对自变量x施加一个非常小的增量$\mathrm dx$时,函数值相应的变化量与$\mathrm dx$之间的关系。当$\mathrm dx$非常小的时候,函数的变化量就接近于在该点处切线的变化量$\mathrm{d}y$。因此,我们可以用这种方式来理解微分:
$$ \frac{\mathrm{d}y}{\mathrm{d}x} = f'(x). \tag{2.1.1}
$$ 在图2.1.1中,我们展示了函数、导数和微分之间的关系。微分实际上描述的是点$M$处切线的斜率;导数则描述的是割线$MN$的斜率。但当$\mathrm{d}x$足够小的时候,切线的斜率和割线的斜率就会非常接近,这就是微分的核心概念。而微分方程,就是描述函数与其导数之间关系的方程。
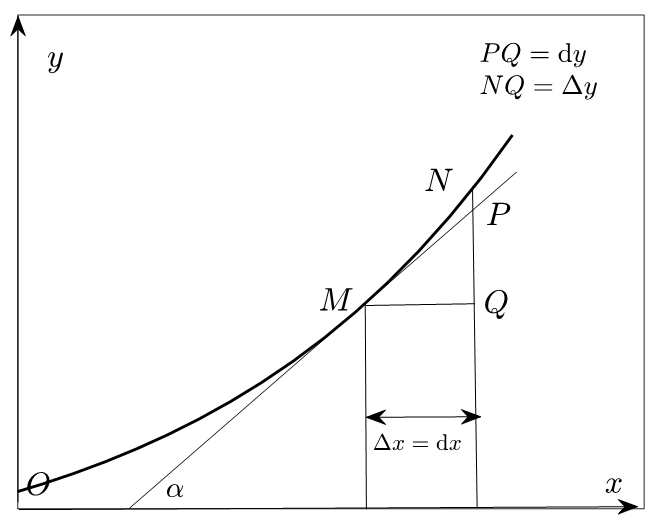
注意:割线斜率等于切线斜率的前提是dx非常小,这是一种极限思想的体现。虽然它们之间存在一个无穷小量PN的差距,但当我们在考虑dx时,这种差异就可以忽略不计了。这就是微分和积分的基本思想。
2.1.2 一阶线性微分方程的解
一阶线性微分方程描述的是怎么一回事呢?它是指形如下方的方程:
$$ \frac{\mathrm{d}y}{\mathrm{d}x} + yP(x) = Q(x). \tag{2.1.2}
$$ 这里的$y$是一个未知函数,而$P$和$Q$是已知的函数。我们的目标是找出$y$的解,即它的通解形式。为了解这个方程,我们通常会使用分离变量积分法和常数变易法这两种方法。首先,我们尝试解一个特殊情况的齐次方程,即当$Q(x)=0$时:
$$ \frac{\mathrm{d}y}{\mathrm{d}x} + yP(x) = 0. \tag{2.1.3}
$$ 通过变量分离和变形,我们可以得到:
$$ \frac{1}{y} \mathrm{d}y = P(x)\mathrm{d}x.\tag{2.1.4}
$$ 接着,对两边进行不定积分,我们可以得到解的通式为$\displaystyle y = C\exp\left{-\int {P(x)} \, \mathrm d{x}\right}$,其中$C$是一个常数。但在一般情况下,$Q(x)$不一定为$0$,所以我们需要将常数$C$替换为一个函数$C(x)$,然后对$y$求导并将其代入原方程中以求得$C(x)$的通解。这就是所谓的常数变易法。有兴趣的读者可以进一步推导出方程的通解为(其中$C$为常数):
$$ y = \exp \left{ -\int {P(x)} \, \mathrm d{x} \right} \left[ \int {Q(x)}\exp \left{ \int {P(x)} \, \mathrm d{x} \right} \, \mathrm d{x} + C \right]. \tag{2.1.5}
$$
注意:这里的定积分符号用于求原函数。这就是为什么我们在高中学习的积分符号应该按照这种方式书写的原因。齐次方程指的是方程右边等于$0$的情况,而非齐次方程则是方程右边不恒等于$0$的情况。解非齐次方程更具有一般性,但很多非齐次方程的解也是基于齐次方程的解进行拓展的。
2.1.3 二阶常系数线性微分方程的解
二阶常系数线性微分方程可以表示为:
$$ f''(x) + pf'(x) + qf(x) = C(x). \tag{2.1.6}
$$ 这个方程关联了二阶导数、一阶导数和函数本身。解决这个方程的一般策略是先考虑对应的齐次方程,即让$C(x)$为$0$:
$$ f''(x) + pf'(x) + qf(x) = 0. \tag{2.1.7}
$$ 解这种二阶常系数齐次线性微分方程时,我们通常使用特征根法。这个方法的关键是求解特征方程:
$$ r^{2} + pr + q = 0. \tag{2.1.8}
$$ 这个齐次方程的解的形式取决于特征方程的根。根据特征方程的不同实根、相同实根、或共轭复根,齐次微分方程的解会有不同的形式:
$$
\left{
\begin{align}
y &= C{1}e^{\alpha{1}x} + C{2}e^{\alpha{2}x} & r{1} = \alpha{1}, r{2} = \alpha{2}\[0.5em]
y &= (C{1}x + C{2})e^{\alpha x}, & r{1} = r{2} = \alpha\[0.5em]
y &= e^{\alpha x}\Big[C{1}\sin\big( \beta x\big) + C{2}\cos \big(\beta x\big)\Big]. & r = \alpha \pm \beta \,\mathrm{i}
\end{align}
\right.\tag{2.1.9}
$$
注意:这里可能有些读者不太明白为什么二次方程的根与齐次方程的解之间会有联系,这正是数学之美的体现之一。如果想检验这个方程的解是否正确,实际上并不难,可以使用 Vieta 定理将 $p$ 和 $q$ 代入,将两个方程统一起来,再通过换元法将其降为一阶微分方程进行验证。
对于一般的二阶非齐次线性微分方程,我们可以根据右侧$C(x)$的形式推导出一个特解。非齐次方程的通解等于齐次方程的通解加上非齐次方程的特解。求微分方程的特解有时需要观察法,但幸运的是,存在两种特殊形式:
$$ \begin{align} C(x) &= P{m}(x) e^{\lambda x},\[0.5em] C(x) &= e^{\lambda x} \Big[ P{m}\cos \big( \omega x \big) + Q_{n}(x)\sin \big( \omega x \big) \Big] \end{align}
$$ 其中,$P_m(x)$是一个$m$次多项式,$Q_n(x)$是一个$n$次多项式。这两种形式的特解分别为:
$$ \begin{align} f(x) &= x{k} P{m}(x)e^{\lambda x},\[0.5em] f(x) &= x^{k} e^{\lambda x} \Big[ P{i}\cos \big( \omega x \big) + Q{i}(x)\sin \big( \omega x \big) \Big]. & i = \max \left{ m,n \right} \end{align} \tag{2.1.11}
$$ 其中$k$的取值取决于特征方程根的个数:如果有两个不同的实根,则$k=2$;如果有两个相同的实根,则$k=1$;如果没有实根,则$k=0$。通过上述形式,我们可以解出二阶线性微分方程。
特征根法和“特解+通解”的策略不仅适用于二阶线性微分方程,也适用于一般的高阶线性微分方程。只要特征方程是多项式,它至少满足韦达定理。在后续的差分方程中,特征根法同样会发挥重要作用。
2.1.4 利用Python求函数的微分与积分
在Python中,我们可以使用Numpy和SciPy这两个库来进行函数的微分和积分计算。下面将通过具体示例来说明如何使用这些库来求解函数的微分和积分。
假设我们需要计算函数f(x) = cos(2πx) * exp(-x) + 1.2在区间[0, 0.7]上的定积分。我们可以使用SciPy库中的quad函数来完成这个任务:
import numpy as np
from scipy.integrate import quad
# 定义函数
def f(x):
return np.cos(2 * np.pi * x) * np.exp(-x) + 1.2
# 计算定积分
integral, error = quad(f, 0, 0.7)
print(f'定积分的结果是:{integral}')
# 定积分的结果是:0.7951866427656943
除了使用SciPy库中的quad函数求解定积分外,我们还可以使用数值积分的方法来近似计算。一种常见的数值积分方法是梯形法则。下面我们将通过一个示例来说明如何使用梯形法则来近似计算函数的定积分。
假设我们需要计算函数f(x) = cos(2πx) * exp(-x) + 1.2在区间[0, 0.7]上的定积分。我们可以使用梯形法则来近似求解:
h=x[1]-x[0]
xn=0.7
s=0
for i in range(1000):
xn1=xn+h
yn=np.cos(2*np.pi*xn)*np.exp(-xn)+1.2
yn1=np.cos(2*np.pi*xn1)*np.exp(-xn1)+1.2
s0=(yn+yn1)*h/2
s+=s0
xn=xn1
s
# 24.31183595181452
对于函数的微分,我们可以使用Numpy库中的gradient函数来近似求解。例如,我们想要求解函数f(x) = x^2在点x = 1处的导数:
import numpy as np
# 定义x的取值范围和步长
x = np.linspace(0, 2, 100)
y = x**2
# 计算导数
dydx = np.gradient(y, x)
# 在x=1处的导数值
derivative_at_1 = dydx[np.argmin(abs(x - 1))]
print(f'在x=1处的导数值是:{derivative_at_1}')
# 在x=1处的导数值是:1.9797979797979792
以上示例展示了如何在Python中求解函数的积分和微分。在实际应用中,可以根据具体问题调整函数表达式、积分区间和微分点等参数。
2.2 使用Scipy和Sympy解微分方程
前面我们见过了求微分方程解析解的一些方法,我们知道,微分方程的解本质上是通过给定函数与微分之间的关系求解出函数的表达式。但是事实上,大多数微分方程是没有解析解的,也就是无法求解出函数的具体解析式。这是不是意味着这样的微分方程不可解呢?也不尽然。在上一章中我们已经见过了,以前我们难以求解的超越方程也是可能给出数值解的,那么微分方程是否也会存在数值解呢?
2.2.1 使用sympy求解微分方程解析解
我们此前介绍的一阶、二阶常系数线性微分方程通解的形式就是一种解析解,但在科学与工程实际中我们遇到的微分方程形式会比这些基本形式更为复杂,条件也更多。事实上多数情况下,大多数微分方程其实是求不出解析解的,只能在不同取值条件下求一个数值解。那么如何编写算法去求数值解才能使精度尽可能提高呢?数值解会随着初始条件而变化,怎么变化呢?函数值又与自变量之间怎么变化呢?
在回答这些问题之前,请让我们先了解一番:如何使用python求解微分方程的解析解呢?但凡涉及到符号运算,通常都是使用sympy库实现。Sympy是一个数学符号运算库。能解决积分、微分方程等各种数学运算方法,用起来也是很简单,效果可以和Matlab媲美。其中内置的Sympy.dsolve方法是解微分方程解析解的一种良好方式,而对于有初始值的微分方程问题,我们通常在求出其通解形式后通过解方程组的方法得到参数。这个方法通过声明符号变量的方式求得最优解。
例如,我们看下面这个例子: 例2.1 使用sympy解下面这个微分方程:
$$ y'' + 2y' + y = x^{2}. \tag{2.2.1}
$$
若使用sympy,我们首先要声明两个符号变量,其中变量y是变量x的函数。代码如下:
from sympy import *
y = symbols('y', cls=Function)
x = symbols('x')
eq = Eq(y(x).diff(x,2)+2*y(x).diff(x,1)+y(x), x*x)
## y''+4y'+29y=0
print(dsolve(eq, y(x)))
这段代码通过sympy中的symbols类创建两个实例化的符号变量x和y,在y中我们通过cls参数声明y是一个scipy.Function对象(也就是说,y是一个函数)。表达微分方程解析解的方法是通过创建一个Eq对象,这个对象分别存储方程左右两边。其中,y(x).diff(x,2)表明y是x的函数,然后需要取函数对x的2阶导数。最后,若想求解函数y的解析式,只需要调用dsolve(eq,y(x))函数即可。代码返回结果:
Eq(y(x), x**2 - 4*x + (C1 + C2*x)*exp(-x) + 6)
可以看到,代码能够给出完整的解析式。之所以还保留了参数C1和C2是因为在求解过程中没有给微分方程指定初值。
我们再来看一个例子,这个例子是使用sympy解一个常微分方程组:
例2.2 使用sympy解下面这个常微分方程组:
$$ \left{ \begin{align} \frac{\mathrm{d}x{1}}{\mathrm{d}t} &= 2x{1} - 3x{2} + 3x{3}, & x{1}(0) = 1\ \frac{\mathrm{d}x{2}}{\mathrm{d}t} &= 4x{1} - 5x{2} + 3x{3}, & x{2}(0) = 2\ \frac{\mathrm{d}x{3}}{\mathrm{d}t} &= 4x{1} - 4x{2} + 2x{3}. & x_{3}(0) = 3\ \end{align} \right. \tag{2.2.2}
$$ 这个方程组里面的$x{1}, x{2}, x_{3}$都是关于$t$的函数,所以需要声明四个符号变量。不同的是,在这里每个函数都指定了初始值,并且三个函数的导数高度相关,该怎么描述这种相关呢?我们来看下面的例子:
t=symbols('t')
x1,x2,x3=symbols('x1,x2,x3',cls=Function)
eq=[x1(t).diff(t)-2*x1(t)+3*x2(t)-3*x3(t),
x2(t).diff(t)-4*x1(t)+5*x2(t)-3*x3(t),
x3(t).diff(t)-4*x1(t)+4*x2(t)-2*x3(t)]
con={x1(0):1, x2(0):2, x3(0):3}
s=dsolve(eq,ics=con)
print(s)
sympy当中内置的symbols工具是可以通过字符串批量创建变量的,这为我们带来了很大的方便。如果需要求解的是一个方程组,则使用列表将每一个方程表达出来即可。这里我们采取了不创建对象的方式,而是直接将方程组移项使每个方程右侧都为0。通过字典的方式保存函数的初始值,并利用ics参数传入dsolve从而得到方程的解。
[Eq(x1(t), 2*exp(2*t) - exp(-t)), Eq(x2(t), 2*exp(2*t) - exp(-t) + exp(-2*t)), Eq(x3(t), 2*exp(2*t) + exp(-2*t))]
结果返回的是一个Eq对象构成的列表,每个对象代表了一个函数的解析式。对于这个例子,大家可以发现:它是一个线性的微分方程组,而针对线性方程我们还可以使用矩阵的形式去表示。所以,这个问题还有第二种写法:
x=Matrix([x1(t),x2(t),x3(t)])
A=Matrix([[2,-3,3],[4,-5,3],[4,-4,2]])
eq=x.diff(t)-A*x
s=dsolve(eq,ics={x1(0):1, x2(0):2, x3(0):3})
print(s)
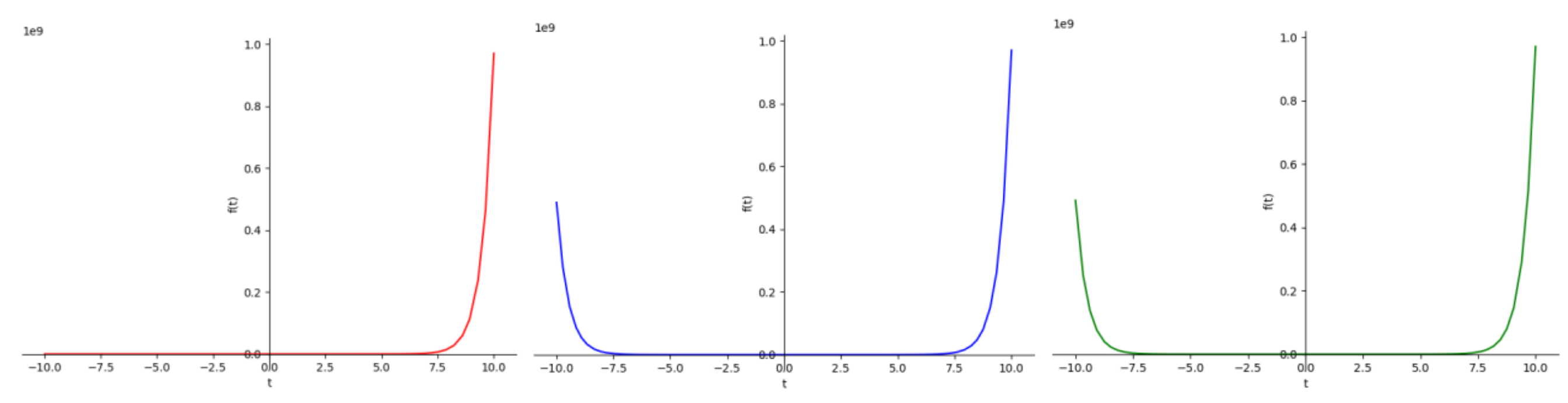
通过sympy中内置的符号矩阵Matrix对象构造函数向量和系数矩阵,通过对方程组矩阵化也可以得出一样的结果。返回值同上。使用sympy中的符号函数绘图得到结果如下:
from sympy.plotting import plot
from sympy import *
t=Symbol('t')
plot(2*exp(2*t) - exp(-t), line_color='red')
plot(2*exp(2*t) - exp(-t) + exp(-2*t), line_color='blue')
plot(2*exp(2*t) + exp(-2*t), line_color='green')
2.2.2 使用scipy求解微分方程数值解
微分方程的数值解是什么样子的呢?虽然大多数微分方程没有解析解,但解析式也并不是唯一可以表示函数的形式。函数的表示还可以用列表法和作图法来表示,而微分方程的数值解也正是像列表一样针对自变量数组中的每一个取值给出相对精确的因变量值。
Python求解微分方程数值解可以使用scipy库中的integrate包。在这当中有两个重要的函数:odeint和solve_ivp。但本质上,从底层来讲求解微分方程数值解的核心原理都是Euler 法和Runge-Kutta 法。关于这两个方法,我们会在后面进行进一步探讨。
我们先来了解一下odeint的用法吧。odeint()函数需要至少三个变量,第一个是微分方程函数,第二个是微分方程初值,第三个是微分的自变量。为了具体了解它的用法,我们通过一个例子来分析:
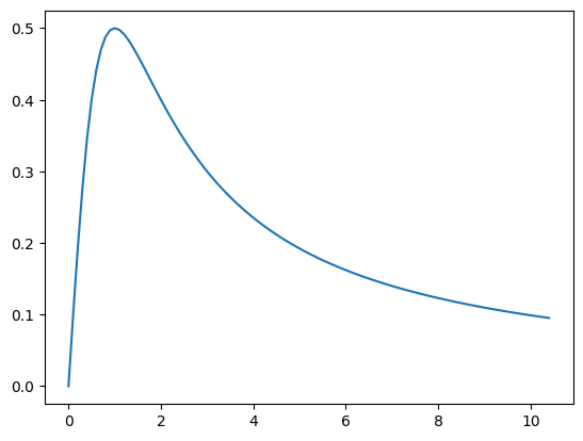
例2.3 使用scipy解下面这个微分方程的数值解:
$$ y' = \frac{1}{1 + x^{2}} - 2y^{2}, \quad y(0) = 0.\tag{2.2.3}
$$
首先需要通过def语句或者lambda表达式定义微分方程的表达式,然后定义微分方程的初值。代码如下:
import matplotlib.pyplot as plt
dy=lambda y,x: 1/(1+x**2)-2*y**2 # y'=1/(1+x^2)-2y^2
'''
def dy(y,x):
return 1/(1+x**2)-2*y**2
'''
x=np.arange(0,10.5,0.1) #从0开始,每次增加0.1,到10.5为止(取不到10.5)
sol=odeint(dy,0,x) # odeint输入:微分方程dy,y的首项(y(0)等于多少),自变量列表
print("x={}\n对应的数值解y={}".format(x,sol.T))
plt.plot(x,sol)
plt.show()
这里odeint函数传入的三个参数分别是函数表达式,函数的初值与自变量。自变量是一个数组,通过numpy.arange生成一个范围在[0, 10.5)的等差数列,公差为0.1。返回的结果sol是针对数组x中每个值的对应函数值,可以通过matplotlib.pyplot绘图得到函数的结果。函数的图像如图所示:
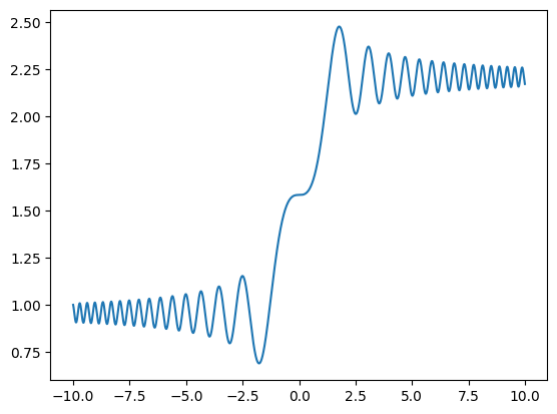
例2.4 使用scipy解下面这个微分方程的数值解:
$$ y'(t) = \sin t^{2}, \quad y(0) = 1 \tag{2.2.4}
$$
仿照例2.3中的代码,这个问题可以改写为:
def dy_dt(y,t):
return np.sin(t**2)
y0=[1]
t = np.arange(-10,10,0.01)
y=odeint(dy_dt,y0,t)
plt.plot(t, y)
plt.show()
得到的结果必然是一个奇函数,图像为:
例2.5 使用scipy解下面这个高阶微分方程的数值解:
$$ \begin{align} y'' - 20(1 - y^{2})y' + y = 0, \quad y(0) = 0, y'(0) = 2 \tag{2.2.5} \end{align}
$$
这很显然是个二阶微分方程,并且不是常系数所以不能直接给出解析解。为了给这个方程做降次,令$u=y'$,那么$y''=u'$,式子就可以代换为:
$$ \left{ \begin{align} u &= y',\[0.5em] u' - 20(1 - y^{2})u + y &= 0,\[0.5em] y(0) &= 0,\[0.5em] u(0) &= 2. \end{align} \right. \tag{2.2.6}
$$
对于微分方程组,我们传入[y,u]两个函数的原函数值,返回的函数值为[y’,u’]。所以,只需要对每个微分表达式给出解析形式就可以了。代码如下:
# odeint是通过把二阶微分转化为一个方程组的形式求解高阶方程的
# y''=20(1-y^2)y'-y
def fvdp(y,t):
'''
要把y看出一个向量,y = [dy0,dy1,dy2,...]分别表示y的n阶导,那么
y[0]就是需要求解的函数,y[1]表示一阶导,y[2]表示二阶导,以此类推
'''
dy1 = y[1] # y[1]=dy/dt,一阶导 y[0]表示原函数
dy2 = 20*(1-y[0]**2) * y[1] - y[0] # y[1]表示一阶微分
# y[0]是最初始,也就是需要求解的函数
# 注意返回的顺序是[一阶导, 二阶导],这就形成了一阶微分方程组
return [dy1, dy2]
# 求解的是一个二阶微分方程,所以输入的时候同时输入原函数y和微分y'
# y[0]表示原函数, y[1]表示一阶微分
# dy1表示一阶微分, dy2表示的是二阶微分
# 可以发现,dy1和y[1]表示的是同一个东西
# 把y''分离变量分离出来: dy2=20*(1-y[0]**2)*y[1]-y[0]
def solve_second_order_ode():
'''
求解二阶ODE
'''
x = np.arange(0,0.25,0.01)#给x规定范围
y0 = [0.0, 2.0] # 初值条件
# 初值[3.0, -5.0]表示y(0)=3,y'(0)=-5
# 返回y,其中y[:,0]是y[0]的值,就是最终解,y[:,1]是y'(x)的值
y = odeint(fvdp, y0, x)
y1, = plt.plot(x,y[:,0],label='y')
y1_1, = plt.plot(x,y[:,1],label='y‘')
plt.legend(handles=[y1,y1_1]) #创建图例
plt.show()
solve_second_order_ode()
定义函数fvdp,传入y的原函数值和一阶导数值(列表传入),返回y的一阶导数值和二阶导数值。初值条件y(0)=0和y'(0)=2传入odeint函数中,自变量是取值[0, 0.25)的一个等距数组。解得的y其实包含两列,第一列是函数值,第二列是导数值。结果的图像如下。
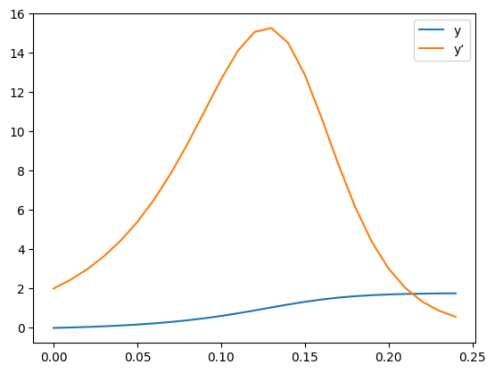
同时,一阶导数$y'(x)$的图像显示出与原函数相似的振荡衰减模式,但相比之下,其变化更加剧烈。这是因为直接受到非线性阻尼项的影响,而$y$则是间接受到影响。
总的来说,这个微分方程组描述了一个非线性阻尼振荡系统,其解的行为随着初始条件和时间的变化而发生变化。在这个例子中,初始条件$y(0) = 0$和$y'(0) = 2$导致了一个振荡衰减的解,这种解在物理学和工程学中很常见,用于描述许多实际系统的动态行为。
我们再来看一个更高阶函数的求解的案例。
例2.6 使用scipy解下面这个高阶微分方程的数值解:
$$ \begin{align} y''' + y'' - y' + y = \cos t, \quad y(0) = 0,~y'(0) = \pi,~y''(0) = 0 \tag{2.2.7} \end{align}
$$
这个案例当然可以和上面一样如法炮制,输入[y, y', y'']返回[y', y'', y''']。这里再次介绍一个案例是想引出Python求微分方程数值解的另一个函数solve_ivp的用法。
首先,仍然是通过换元法对函数进行定义:
def f(y,t):
dy1 = y[1]
dy2 = y[2]
dy3 = -y[0]+dy1-dy2-np.cos(t)
return [dy1,dy2,dy3]
Solve_ivp函数的用法与odeint非常类似,只不过比odeint多了两个参数。一个是t_span参数,表示自变量的取值范围;另一个是method参数,可以选择多种不同的数值求解算法。常见的内置方法包括RK45, RK23, DOP853, Radau, BDF等多种方法,通常使用RK45多一些。它的使用方法与odeint对比起来很类似,对这个问题进行代码实现如下:
def solve_high_order_ode():
'''
求解高阶ODE
'''
t = np.linspace(0,6,1000)
tspan = (0.0, 6.0)
y0 = [0.0, pi, 0.0]
# 初值[0,1,0]表示y(0)=0,y'(0)=1,y''(0)=0
# 返回y, 其中y[:,0]是y[0]的值 ,就是最终解 ,y[:,1]是y'(x)的值
y = odeint(f, y0, t)
y_ = solve_ivp(f,t_span=tspan, y0=y0, t_eval=t)
plt.subplot(211)
l1, = plt.plot(t,y[:,0],label='y(0) Initial Function')
l2, = plt.plot(t,y[:,1],label='y(1) The first order of Initial Function')
l3, = plt.plot(t,y[:,2],label='y(2) The second order of Initial Function')
plt.legend(handles=[l1,l2,l3])
plt.grid('on')
plt.subplot(212)
l4, = plt.plot(y_.t, y_.y[0,:],'r--', label='y(0) Initial Function')
l5,= plt.plot(y_.t,y_.y[1,:],'g--', label='y(1) The first order of Initial Function')
l6, = plt.plot(y_.t,y_.y[2,:],'b-', label='y(2) The second order of Initial Function')
plt.legend(handles=[l4,l5,l6]) # 显示图例
plt.grid('on')
plt.show()
solve_high_order_ode()
solve_ivp 和 odeint 两个函数都可以解偏微分方程,但是solve_ivp可以不考虑参数顺序,odeint必须要考虑参数顺序(经验之谈)。感谢学习者提问&勘误。
这里通过matplotlib.pyplot中提供的绘图接口绘制了两个数值解的图像。由于没有设置method参数,这里默认solve_ivp使用RK45(4-5阶 Runge-Kutta 法)方法进行求解。所解得的结果如图所示:
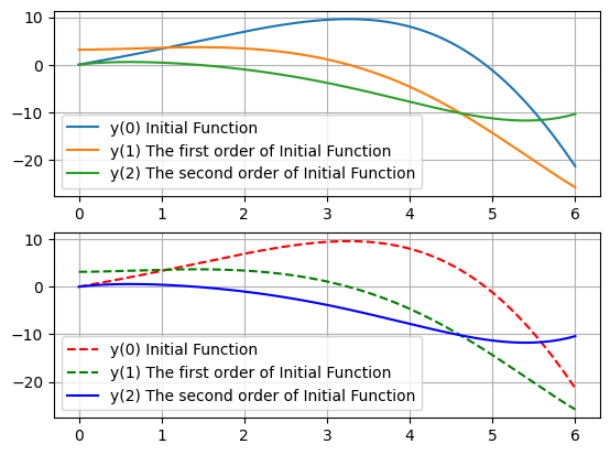
odeint求解得到的结果,下半部分是由solve_ivp得到的结果,二者大差不差。一般来说对于普通的微分方程odeint与solve_ivp得到的结果差异不会太大,但有些情况下函数的微分容易发散,就会导致求解结果出现比较大的差异。odeint内置的原理也是4-5阶 Runge-Kutta 法,版本比较早所以求解也相对较为稳定。但solve_ivp则是后来新增的方法,有可能出现不太稳定的现象,内置方法较多所以也更加灵活。
Python求解微分方程组的模式有两种:一是采用基于基本原理自己写相关函数,这样操作比较繁琐,但是对于整个的求解过程会比较清晰明了;第二就是利用python下面的ode求解器,熟悉相关的输入输出,就可以完成数值求解。基于这个demo,在不同方向领域可以套用不同的微分方程组模型,进行仿真求解。但无论是常微分方程组还是偏微分方程组,使用的都是同一套思路,就是用差分代替微分。
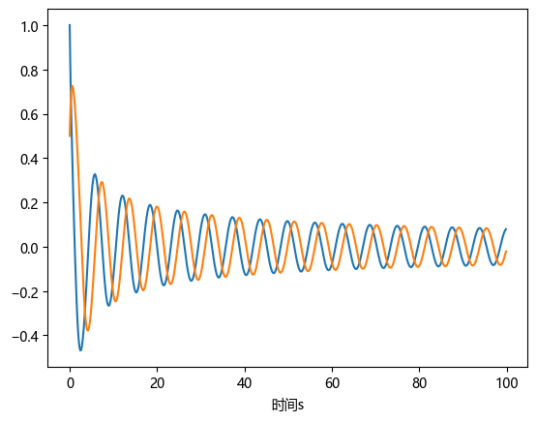
例2.7 使用scipy解下面这个微分方程组的数值解:
$$ \left{ \begin{align} x'(t) &= - x^{3} - y, \ y'(t) &= -y^{3} + x. \end{align} \right.
$$
这个例子和例2.2很像,但不同的是这是也一个非线性方程组。那么,输入就需要以数组的形式传入[x, y]两个函数的函数值,返回它们的导数值。这里使用solve_ivp对这个方程组进行求解如下:
def fun(t, w):
x = w[0]
y = w[1]
return [-x**3-y,-y**3+x]
# 初始条件
y0 = [1,0.5]
yy = solve_ivp(fun, (0,100), y0, method='RK45',t_eval = np.arange(0,100,0.2) )
t = yy.t
data = yy.y
plt.plot(t, data[0, :])
plt.plot(t, data[1, :])
plt.xlabel("时间s")
plt.show()
绘制图像如图所示:
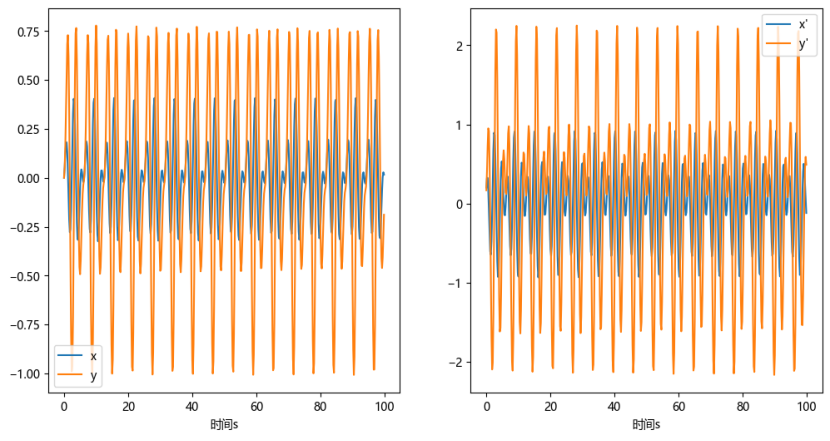
例2.8 使用 scipy 解下面这个微分方程组的数值解:
$$ \left{ \begin{align} x''(t) + y'(t) + 3x(t) &= \cos(2t), \[0.5em] y''(t) - 4x'(t) + 3y(t) &= \sin(2t), \[0.5em] x'(0) = \frac{1}{5}, y'(0) = \frac{6}{5}, x(0) &= y(0) = 0. \end{align} \right.
$$
这个例子就比较有趣了,在方程组里面涉及到了两个函数的导数怎么求解呢?本质上还是要使用换元法。完全可以令$u=x’$, $v=y’$,然后带入到方程组中把一个二元二阶微分方程组变为四元一阶微分方程组。代码实现如下所示:
def fun(t, w):
x = w[0]
y = w[1]
dx = w[2]
dy = w[3]
# 求导以后[x,y,dx,dy]变为[dx,dy,d2x,d2y]
# d2x为w[2],d2y为w[5]
return [dx,dy,-dy-3*x+np.cos(2*t),4*dx-3*y+np.sin(2*t)]
# 初始条件
y0 = [0,0,1/5,1/6]
yy = solve_ivp(fun, (0,100), y0, method='RK45',t_eval = np.arange(0,100,0.2) )
t = yy.t
data = yy.y
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(t, data[0, :])
plt.plot(t, data[1, :])
plt.legend(['x','y'])
plt.xlabel("时间s")
plt.subplot(1,2,2)
plt.plot(t, data[2, :])
plt.plot(t, data[3, :])
plt.legend(["x' ","y' "])
plt.xlabel("时间s")
plt.show()
得到的图像如图所示:
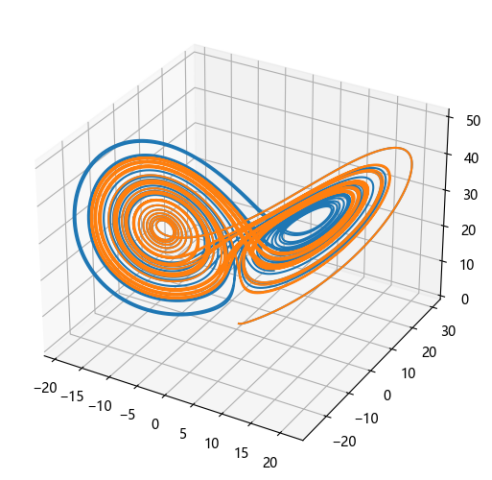
例2.9 使用scipy求解洛伦兹系统的数值解,参数与初始值自设:
$$ \left{ \begin{align} \frac{\mathrm{d}x}{\mathrm{d}t} &= p(y - x), \ \frac{\mathrm{d}x}{\mathrm{d}t} &= x(r - z), \ \frac{\mathrm{d}z}{\mathrm{d}t} &= xy - bz, \end{align} \right.
$$
有前面的例子作为经验,我们知道x y z都是函数其余的都是参数。利用solve_ivp很容易求解这个系统的代码:
import numpy as np
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
def dmove(Point, t, sets):
p, r, b = sets
x, y, z = Point
return np.array([p*(y-x), x*(r-z), x*y-b*z])
t = np.arange(0, 30, 0.001)
P1 = odeint(dmove, (0., 1., 0.), t, args=([10., 28., 3.],))
P2 = odeint(dmove, (0., 1.01, 0.), t, args=([10., 28., 3.],))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(P1[:,0], P1[:,1], P1[:,2])
ax.plot(P2[:,0], P2[:,1], P2[:,2])
plt.show()
Mpl_toolkits.mplot3d提供了进行三维曲线、曲面绘制的函数,这里使用里面提供的三维坐标系绘制洛伦兹系统中点的运动轨迹。我们这里基于不同的初值绘制了两个点的轨迹P1和P2,并展示在图中:
2.3 偏微分方程的数值求解
偏微分方程是针对多元函数来说的,它在物理学中有着很深刻的现实意义。但是,偏微分方程往往比常微分方程更难求解,并且Python也没有提供偏微分方程的专用工具包。怎么求解这些偏微分方程呢?我们要始终把握一个思想:就是把连续的问题离散化。这一节会通过一系列的物理案例来看到Python如何求解一些典型的偏微分方程。
2.3.1 偏微分方程数值解的理论基础
偏微分方程实际上就是由多元函数、自变量与多元函数的偏导数及高阶偏导数之间构成的方程。它在工程中很多地方都有深刻应用,比如波动力学、热学、电磁学等。我们常研究的就是二元函数的二阶偏微分方程,其基本形式为:
$$ A \frac{ \partial^{2} f }{ \partial x^{2} } + 2B \frac{ \partial^{2} f }{ \partial x\partial y } + C \frac{ \partial^{2} f }{ \partial y^{2} } + D\frac{ \partial f }{ \partial x } + E \frac{ \partial f }{ \partial y } + Ff = 0. \tag{2.3.1}
$$ 在方程中,如果$A$、$B$、$C$三个常系数不全为$0$,定义判别式$\Delta = B^{2} - 4AC$,当判别式大于$0$称其为双曲线式方程;若判别式等于$0$,则称其为抛物线式方程;若判别式小于$0$,则称其为椭圆式方程。有关于这几类方程的基本性质与边界条件等内容请感兴趣的读者自行参考偏微分方程领域的书籍,我们的主要目光更多的聚焦在它的应用上。
刚刚我们说到,二阶偏微分方程主要有三类:椭圆方程,抛物方程和双曲方程。双曲方程描述变量以一定速度沿某个方向传播,常用于描述振动与波动问题。椭圆方程描述变量以一定深度沿所有方向传播,常用于描述静电场、引力场等稳态问题。抛物方程描述变量沿下游传播,常用于描述热传导和扩散等瞬态问题。它们都在工程中有实际应用。
偏微分方程的定解问题通常很难求出解析解,只能通过数值计算方法对偏微分方程的近似求解。常用偏微分方程数值解法有包括有限差分方法、有限元方法、有限体方法、共轭梯度法,等等。在使用这些数值方法时通常先对问题的求解区域进行网格剖分,然后将定解问题离散为代数方程组,求出在离散网格点上的近似值。
偏微分方程的典型应用有很多。描述热源传热过程中温度变化的热传导方程本质上是一个抛物类微分方程。大名鼎鼎的韦东奕大神所着重研究的纳维-斯托克斯方程,所描述的是流体流速与流体密度、压力、外阻力之间的关系,在机械工程、能源工程等制造领域有着重要应用。还有电磁场中非常重要的麦克斯韦方程组,本质上也是偏微分方程。下面我们会根据一系列的具体应用来看如何去构建与求解微分方程。
2.3.2 偏微分方程数值解的应用案例
本节参考https://youcans.blog.csdn.net/article/details/119755450,特别鸣谢!
解偏微分方程由于缺少特定的工具包,更多的情况下需要自己写代码求解。这就迫使我们不得不理解微分方程求解的核心思想:以离散代替连续,用差分逼近微分。 一类有限差分法求解偏微分方程数值解的步骤包括如下几步:
- 定义初始条件函数 $U(x,0)$;
- 输入模型参数,对于待求解函数$F(x,t)$定义求解的时间域$(\mathrm{tStart}, \mathrm{tEnd})$和空间域$(\mathrm{xMin}, \mathrm{xMax})$,设置差分步长$\mathrm{d}t$, $\mathrm{nNodes}$;
- 初始化解空间;
- 根据递推规则递推求解差分方程在区间
[xa, xb]的数值解,获得网格节点的处的函数值,最终填满整个解空间。
我们首先用一个常微分方程的应用揭示这一过程。
例2.10 使用偏微分方程对RC电路进行建模,分析电容放电过程中电量随时间的变化。
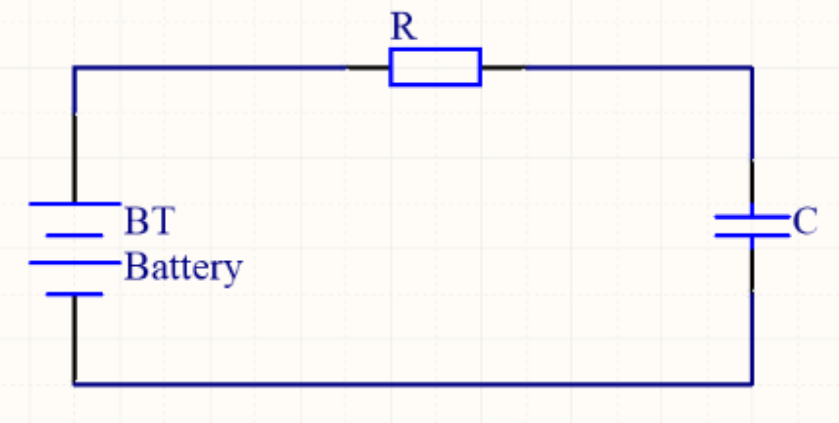
$$ \left{ \begin{align} IR + \frac{Q}{C} &= 0, \ I &= \frac{\mathrm{d}Q}{\mathrm{d}t}, \end{align} \right. \tag{2.3.2}
$$
式子中$I$代表了电流,$R$代表电阻值,$Q$代表电容电量,$C$代表电容值。为什么这个电路叫$RC$电路?这不仅仅是由于电路中包括电阻和电容两个核心元件,也是指$\tau = RC$的乘积是一个重要的参数。令,这个常微分方程存在很明显的解析解:
$$ Q(t) = Q_{0} e^{- t/\tau}. \tag{2.3.3}
$$ 那么我们为什么还要来谈这个案例?我想通过这个案例来给大家讲述一下把一个连续问题离散化的方法。我们先从一阶微分方程的计算原理说起。将一阶微分方程离散化,实际上也就是把它写成迭代、差分的形式。对于一个连续的问题有
$$
\left{
\begin{align}
\frac{\mathrm{d}y}{\mathrm{d}t} &= f(y, t), \[0.5em]
y{0}(t{0}) &= y_{0}.
\end{align}
\right. \tag{2.3.4}
$$ 画出$y(t)$的图像如图所示:
$$ y{n+1} = y{n} + \frac{f(y{n}, t{n}) + f(y{n+1}, t{n+1})}{2} h. \tag{2.3.5}
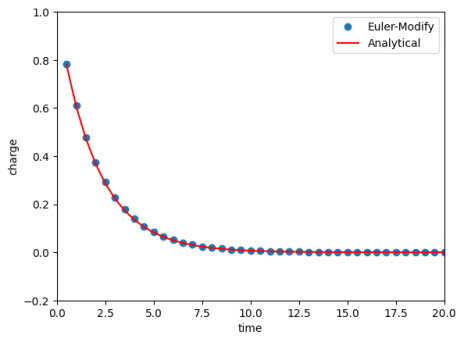
$$ 那么对于例2.10中的电容放电过程,这个问题的代码可以这样写:
import numpy as np
import matplotlib.pyplot as plt
rc = 2.0 #设置常数
dt = 0.5 #设置步长
n = 1000 #设置分割段数
t = 0.0 #设置初始时间
q = 1.0 #设置初始电量
#先定义三个空列表
qt=[] #用来盛放差分得到的q值
qt0=[] #用来盛放解析得到的q值
time = [] #用来盛放时间值
for i in range(n):
t = t + dt
q1 = q - q*dt/rc #qn+1的近似值
q = q - 0.5*(q1*dt/rc + q*dt/rc) #差分递推关系
q0 = np.exp(-t/rc) #解析关系
qt.append(q) #差分得到的q值列表
qt0.append(q0) #解析得到的q值列表
time.append(t) #时间列表
plt.plot(time,qt,'o',label='Euler-Modify') #差分得到的电量随时间的变化
plt.plot(time,qt0,'r-',label='Analytical') #解析得到的电量随时间的变化
plt.xlabel('time')
plt.ylabel('charge')
plt.xlim(0,20)
plt.ylim(-0.2,1.0)
plt.legend(loc='upper right')
plt.show()
这个案例我们没有用任何包里面的微分方程求解器,纯手写的情况下解了这个微分方程。它的结果如图所示:
例2.11 一维热传导方程是一个典型的抛物型二阶偏微分方程。设$u(x,t)$表示在时间$t$,空间$x$处的温度,则根据傅里叶定律(单位时间内流经单位面积的热量和该处温度的负梯度成正比),可以导出热传导方程:
$$ \frac{ \partial u }{ \partial t } = \lambda \frac{ \partial^{2} u }{ \partial x^{2} }
$$ 其中$\lambda$称为热扩散率,$k,C,p$分别为热导率,比热和质量密度,是由系统本身确定的常量。问题的形式为:
$$ \begin{align} &\frac{ \partial u(x, t) }{ \partial t } = \frac{ \partial^{2} u(x,t) }{ \partial x^{2} } \[0.5em] & 0 \leqslant t \leqslant 1000, 0 \leqslant x \leqslant 3\[0.5em] & u(x,0) = 4x(3-x)\[0.5em] & u(0,t) = u(3, t) = 0\[0.5em] \end{align} \tag{2.3.7}
$$ 请求解这个问题的数值解。
一元函数的微分方程可以绘制曲线,那么二元函数的偏微分方程应该就可以绘制曲面。那么,怎么对这个问题进行离散化呢?对于一个一般的二阶抛物型偏微分方程:
$$ \begin{align} &\frac{ \partial u(x, t) }{ \partial t } = \frac{ \partial^{2} u(x,t) }{ \partial x^{2} } \[0.5em] & 0 \leqslant t \leqslant T, 0 \leqslant x \leqslant l\[0.5em] & u(x,0) = f(x)\[0.5em] & u(0,t) = g{1}(t)\[0.5em] & u(3, t) = g{2}(t)\[0.5em] \end{align} \tag{2.3.7}
$$ 对时间和空间的一阶偏导数微分是容易离散化的:
$$ \begin{align} \frac{ \partial u(x{i}, t{k}) }{ \partial t{k} } &\implies \frac{u(x{i}, t{k+1}) - u(x{i}, t{k})}{\Delta t}, \ \frac{ \partial u(x{i}, t{k}) }{ \partial x{i} } &\implies \frac{u(x{i+1}, t{k}) - u(x{i}, t{k})}{\Delta x}. \ \end{align}
$$ 那么,对于空间的二阶微分,可以看作是一阶微分的再微分:
$$ \frac{ \partial^{2} u(x{i}, t{k}) }{ \partial x{i}^{2} } \implies \frac{\displaystyle \frac{u(x{i+1}, t{k}) - u(x{i}, t{k})}{\Delta x} - \frac{u(x{i}, t{k}) - u(x{i-1}, t_{k})}{\Delta x}}{\Delta x}. \tag{2.3.10}
$$ 也就是$\displaystyle \frac{u(x{i+1}, t{k}) + u(x{i-1}, t{k}) - 2u(x{i}, t{k})}{(\Delta x)^{2}}$。
了解了这个原理,我们将例2.11中的边界条件和迭代规则进行翻译如下:
import numpy as np
import matplotlib.pyplot as plt
h = 0.1#空间步长
N =30#空间步数
dt = 0.0001#时间步长
M = 10000#时间的步数
A = dt/(h**2) #lambda*tau/h^2
U = np.zeros([N+1,M+1])#建立二维空数组
Space = np.arange(0,(N+1)*h,h)#建立空间等差数列,从0到3,公差是h
#边界条件
for k in np.arange(0,M+1):
U[0,k] = 0.0
U[N,k] = 0.0
#初始条件
for i in np.arange(0,N):
U[i,0]=4*i*h*(3-i*h)
#递推关系
for k in np.arange(0,M):
for i in np.arange(1,N):
U[i,k+1]=A*U[i+1,k]+(1-2*A)*U[i,k]+A*U[i-1,k]
将解空间抽象为以时间为横坐标、空间为纵坐标的网格,翻译时间与空间的边界条件,对于网格内每个点使用二重循环遍历每个点,根据差分后的迭代方程进行演化。不同时刻的温度随空间坐标的变化图像如下:
plt.plot(Space,U[:,0], 'g-', label='t=0',linewidth=1.0)
plt.plot(Space,U[:,3000], 'b-', label='t=3/10',linewidth=1.0)
plt.plot(Space,U[:,6000], 'k-', label='t=6/10',linewidth=1.0)
plt.plot(Space,U[:,9000], 'r-', label='t=9/10',linewidth=1.0)
plt.plot(Space,U[:,10000], 'y-', label='t=1',linewidth=1.0)
plt.ylabel('u(x,t)', fontsize=20)
plt.xlabel('x', fontsize=20)
plt.xlim(0,3)
plt.ylim(-2,10)
plt.legend(loc='upper right')
plt.show()
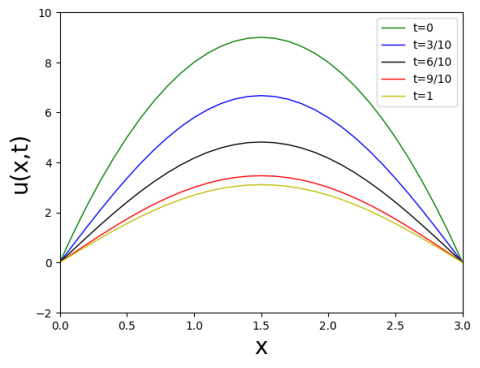
- 在 $\displaystyle t = \frac{3}{10}$(蓝线)时,曲线稍微上升,表明温度在增加。
- 到了 $\displaystyle t=\frac{6}{10}$(黑线),温度继续上升,但上升的速度似乎开始减缓。
- $\displaystyle t = \frac{9}{10}$(红线)时,曲线达到高点之后开始回落,这可能意味着一个冷却过程的开始。
- 到 $t = 1$(黄线)时,温度分布与时相比$t=0$明显增高,但比$\displaystyle t = \frac{9}{10}$时有所降低,显示了经过一段时间后温度分布的稳定状态。
整体上,这些曲线描述了温度如何随着时间从初始状态演变到一个稳态分布。这种分析对于理解热传导、扩散过程,以及如何在时间上控制温度分布都是非常有用的。图形的$\mathrm{y}$轴显示的是$u(x,t)$,即位置$x$在时间$t$的温度,而$\mathrm{x}$轴表示空间坐标。曲线下方较深的颜色表示较低的温度值,而曲线顶部较浅的颜色表示较高的温度值。通过设置坐标轴的范围和图例的位置,这张图为观察者提供了清晰的数据解读。
图中的$\mathrm{y}$轴标记为 ,表示在位置$x$和时间$t$的温度,$\mathrm{x}$轴标记为$x$表示空间坐标。可视窗口的设置为$x$值从$0$到$3$,$u(x,t)$的值从$-2$到$10$。
将整个网格空间的温度分布热力图绘制如图所示:
#温度等高线随时空坐标的变化,温度越高,颜色越偏红
extent = [0,1,0,3] #时间和空间的取值范围
levels = np.arange(0,10,0.1)#温度等高线的变化范围0-10,变化间隔为0.1
plt.contourf(U,levels,origin='lower',extent=extent,cmap=plt.cm.jet)
plt.ylabel('x', fontsize=20)
plt.xlabel('t', fontsize=20)
plt.show()
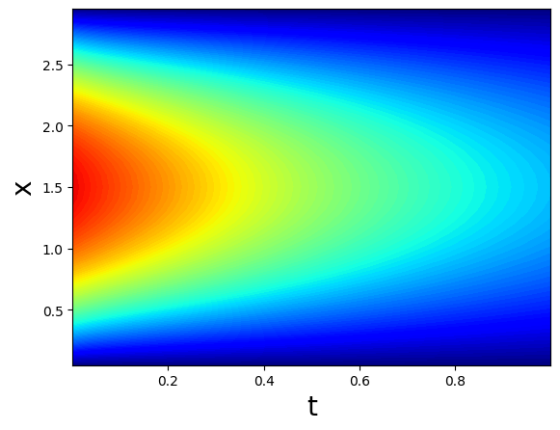
等温线的密集区表示温度变化较大的区域,而等温线的稀疏区则表示温度变化较小的区域。从热力图中我们可以推断,最高温区域集中在图的右上角,而最低温区域则在左下角。通过色彩的深浅变化,我们可以直观地看到温度在空间中如何变化以及时间对这种分布的影响。
例2.12 平流过程是大气运动中重要的过程。平流方程(Advection equation)描述某一物理量的平流作用而引起局地变化的物理过程,最简单的形式是一维平流方程。
$$ \begin{align} & \frac{ \partial u }{ \partial t } + v \frac{ \partial u }{ \partial x } = 0,\[0.5em] & u(x,0) = F(x). \end{align} \tag{2.3.11}
$$ 式中$u$为某物理量,$v$为系统速度,$x$为水平方向分量,$t$为时间。该方程可以求得解析解:
$$ u(x,t) = F(x-vt). \tag{2.3.12}
$$ 考虑一维线性平流偏微分方程的数值解法,采用有限差分法求解。简单地, 采用一阶迎风格式的差分方法(First-order Upwind),一阶导数的差分表达式为:
$$ \begin{align} \left. \frac{ \partial u }{ \partial x } \right|{i,j} &\implies \frac{u{i+1,j} - u{i,j}}{\Delta x}, \[0.5em] u{i,j+1} &= u{i,j} - v\frac{\Delta t}{\Delta x}\big( u{i,j} - u_{i-1,j} \big). \end{align} \tag{2.3.13}
$$ 代码实现如下:
# eg.3.
import numpy as np
import matplotlib.pyplot as plt
# 初始条件函数 U(x,0)
def funcUx_0(x, p):
u0 = np.sin(2 * (x-p)**2)
return u0
# 输入参数
v1 = 1.0 # 平流方程参数,系统速度
p = 0.25 # 初始条件函数 u(x,0) 中的参数
tc = 0 # 开始时间
te = 1.0 # 终止时间: (0, te)
xa = 0.0 # 空间范围: (xa, xb)
xb = np.pi
dt = 0.02 # 时间差分步长
nNodes = 100 # 空间网格数
# 初始化
nsteps = round(te/dt)
dx = (xb - xa) / nNodes
x = np.arange(xa-dx, xb+2*dx, dx)
ux_0 = funcUx_0(x, p)
u = ux_0.copy() # u(j)
ujp = ux_0.copy() # u(j+1)
# 时域差分
for i in range(nsteps):
plt.clf() # 清除当前 figure 的所有axes, 但是保留当前窗口
# 计算 u(j+1)
for j in range(nNodes + 2):
ujp[j] = u[j] - (v1 * dt/dx) * (u[j] - u[j-1])
# 更新边界条件
u = ujp.copy()
u[0] = u[nNodes + 1]
u[nNodes+2] = u[1]
tc += dt
# 绘图
plt.plot(x, u, 'b-', label="v1= 1.0")
plt.axis((xa-0.1, xb + 0.1, -1.1, 1.1))
plt.xlabel("x")
plt.ylabel("U(x)")
plt.legend(loc=(0.05,0.05))
plt.show()
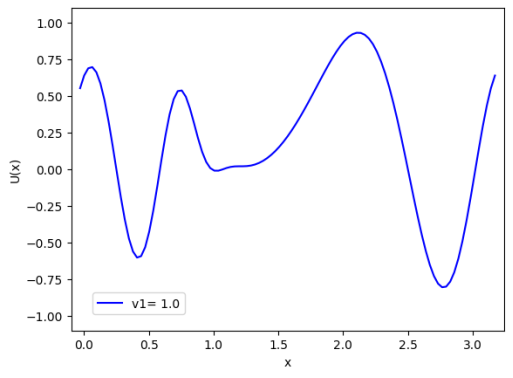
注意到曲线在$\mathrm{x}$轴的不同位置出现了波峰和波谷,这表明了函数值随位置的变化并非均匀。由于是一阶迎风格式的数值解法,我们可能会观察到与理论解相比有一定程度的数值扩散或者数值耗散,这是由于一阶方法在数值传输过程中的固有特性。
在这个示例中,曲线的形状可能表示了经过一段时间演化后,平流作用在初始条件$U(x,0)$上的效果。如果初始波形移动的速度是$v_{1}$,那么这个图形可能表明波形随着时间的推进而向右移动。然而,由于是一阶迎风差分,我们也可以预期波形会有一定程度的变形,这在实际中表现为波峰变得不那么尖锐,以及波形整体变得更加平坦。这是数值方法的离散化误差导致的结果。
这个数值解可以帮助理解平流方程在数值模拟中的行为,特别是当理论解难以获得时,数值方法提供了一种有效的途径来近似解决实际问题。
例2.13 波动方程(wave equation)是典型的双曲偏微分方程,广泛应用于声学,电磁学,和流体力学等领域,描述自然界中的各种的波动现象,包括横波和纵波,例如声波、光波和水波。考虑如下二维波动方程的初边值问题:
$$ \begin{align} \frac{ \partial^{2} u }{ \partial t^{2} } &= c^{2} \left( \frac{ \partial^{2} u }{ \partial x^{2} } + \frac{ \partial^{2} u }{ \partial y^{2} } \right), \[0.5em] \frac{ \partial u(0,x,y) }{ \partial t } &= 0,\[0.5em] u(x,y,0) &= u{0}(x,y),\[0.5em] u(0,y,t) &= u{a}(t), \quad u(1,y,t) = u{b}(t),\[0.5em] u(x,0,t) &= u{c}(t), \quad u(x,1,t) = u_{d}(t),\[0.5em] \end{align}\tag{2.3.14}
$$ 式中:$u$ 是振幅;$c$ 为波的传播速率,$c$ 可以是固定常数,或位置的函数 $c(x,y)$,也可以是振幅的函数 $c(u)$。
考虑二维波动偏微分方程的数值解法,采用有限差分法求解。简单地, 采用迎风法的三点差分格式, 将上述的偏微分方程离散为差分方程:
$$ \begin{align} &\frac{u{i,j,k} + u{i,j,k+1} - 2u{i,j,k}}{(\Delta t)^{2}} \&= c^{2} \left[ \frac{u{i-1,j,k} + u{i+1,j,k} - 2u{i,j,k}}{(\Delta x)^{2}} + \frac{u{i,j-1,k} + u{i,j+1,k} - 2u_{i,j,k}}{(\Delta y)^{2}} \right]. \tag{2.3.15} \end{align}
$$ 可以得到迭代规则为:
$$ \begin{align} r{x} &= c^{2} \frac{(\Delta t)^{2}}{(\Delta x)^{2}}, \[0.5em] r{y} &= c^{2} \frac{(\Delta t)^{2}}{(\Delta y)^{2}}, \[0.5em] u{i,j,k+1} &= r{x}\big( u{i-1,j,k} + u{i+1,j,k} \big) \ &+ 2\big( 1 - r{x} - r{y} \big) u{i,j,k} + r{y} \big( u{i,j-1,k} + u{i,j+1,k} \big) - u_{i,j,k-1}. \end{align} \tag{2.3.16}
$$ 它的代码实现如下:
import numpy as np
import matplotlib.pyplot as plt
# 模型参数
c = 1.0 # 波的传播速率
tc, te = 0.0, 1.0 # 时间范围,0<t<te
xa, xb = 0.0, 1.0 # 空间范围,xa<x<xb
ya, yb = 0.0, 1.0 # 空间范围,ya<y<yb
# 初始化
c2 = c*c # 方程参数
dt = 0.01 # 时间步长
dx = dy = 0.02 # 空间步长
tNodes = round(te/dt) # t轴 时序网格数
xNodes = round((xb-xa)/dx) # $\mathrm{x}$轴 空间网格数
yNodes = round((yb-ya)/dy) # $\mathrm{y}$轴 空间网格数
tZone = np.arange(0, (tNodes+1)*dt, dt) # 建立空间网格
xZone = np.arange(0, (xNodes+1)*dx, dx) # 建立空间网格
yZone = np.arange(0, (yNodes+1)*dy, dy) # 建立空间网格
xx, yy = np.meshgrid(xZone, yZone) # 生成网格点的坐标 xx,yy (二维数组)
# 步长比检验(r>1 则算法不稳定)
r = 4 * c2 * dt*dt / (dx*dx+dy*dy)
print("dt = {:.2f}, dx = {:.2f}, dy = {:.2f}, r = {:.2f}".format(dt,dx,dy,r))
assert r < 1.0, "Error: r>1, unstable step ratio of dt2/(dx2+dy2) ."
rx = c*c * dt**2/dx**2
ry = c*c * dt**2/dy**2
# 绘图
fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(111, projection='3d')
# 计算初始值
U = np.zeros([tNodes+1, xNodes+1, yNodes+1]) # 建立三维数组
U[0] = np.sin(6*np.pi*xx)+np.cos(4*np.pi*yy) # U[0,:,:]
U[1] = np.sin(6*np.pi*xx)+np.cos(4*np.pi*yy) # U[1,:,:]
surf = ax1.plot_surface(xx, yy, U[0,:,:], rstride=2, cstride=2, cmap=plt.cm.coolwarm)
# 有限差分法求解
for k in range(2,tNodes+1):
for i in range(1,xNodes):
for j in range(1,yNodes):
U[k,i,j] = rx*(U[k-1,i-1,j]+U[k-1,i+1,j]) + ry*(U[k-1,i,j-1]+U[k-1,i,j+1])\
+ 2*(1-rx-ry)*U[k-1,i,j] -U[k-2,i,j]
surf = ax1.plot_surface(xx, yy, U[k,:,:], rstride=2, cstride=2, cmap='rainbow')
ax1.set_xlim3d(0, 1.0)
ax1.set_ylim3d(0, 1.0)
ax1.set_zlim3d(-2, 2)
ax1.set_title("2D wave equationt (t= %.2f)" % (k*dt))
ax1.set_xlabel("x")
ax1.set_ylabel("y")
plt.show()
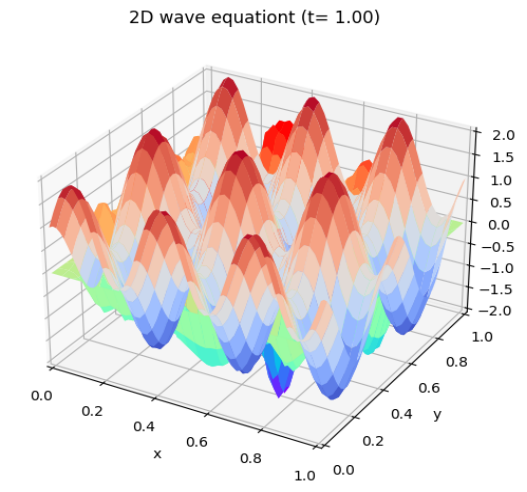
这个函数是一个三元函数,实际上是可以做出一个曲面随时间变化的动画的。大家可以尝试使用matplotlib提供的动画功能进行绘制,这里展示其中一个瞬时状态:
$$ \begin{align} \frac{ \partial u }{ \partial t } &= \lambda \left( \frac{ \partial^{2} u }{ \partial x^{2} + \frac{ \partial^{2} u }{ \partial y^{2} } } \right) + q{v}\[0.5em] \frac{ \partial u(0, x, y) }{ \partial t } &= 0\[0.5em] u(x,y,0) &= u{0}(x,y),\[0.5em] u(0,y,t) &= u{a}(t), \quad u(1,y,t) = u{b}(t),\[0.5em] u(x,0,t) &= u{c}(t), \quad u(x,1,t) = u{d}(t).\[0.5em] \end{align} \tag{2.3.17}
$$ 类似的,同上一个例子中的有限差分法,我们将这个方程离散化可以得到:
$$ \begin{align} r{x} &= \lambda^{2} \frac{(\Delta t)^{2}}{(\Delta x)^{2}}, \[0.5em] r{y} &= \lambda^{2} \frac{(\Delta t)^{2}}{(\Delta y)^{2}}, \[0.5em] u{i,j,k+1} &= r{x}\big( u{i-1,j,k} + u{i+1,j,k} \big) \ &+ 2\big( 1 - r{x} - r{y} \big) u{i,j,k} + r{y} \big( u{i,j-1,k} + u{i,j+1,k} \big) - u_{i,j,k-1}. \end{align} \tag{2.3.18}
$$ 事实上,这个方程还有一种矩阵形式:
$$ U{k+1} = U{k} + r{x}AU{k} + r{y}BU{k} + q_{v}\Delta t, \tag{2.3.19}
$$ 其中
$$ A = \left[ \begin{matrix} -2 & -1 & 0 & \cdots & 0 & 0\ 1 & -2 & 1 & \cdots & 0 & 0\ 0 & 1 & -2 & \cdots & 0 & 0\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots\ 0 & 0 & 0 & \cdots & 1 & -2 \end{matrix} \right]{N{x} \times N{x}}, \quad B = \left[ \begin{matrix} -2 & -1 & 0 & \cdots & 0 & 0\ 1 & -2 & 1 & \cdots & 0 & 0\ 0 & 1 & -2 & \cdots & 0 & 0\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots\ 0 & 0 & 0 & \cdots & 1 & -2 \end{matrix} \right]{N{y} \times N{y}}. \tag{2.3.20}
$$ 我们这次就用这个矩阵形式去进行偏微分方程的求解:
import numpy as np
import matplotlib.pyplot as plt
def showcontourf(zMat, xyRange, tNow): # 绘制等温云图
x = np.linspace(xyRange[0], xyRange[1], zMat.shape[1])
y = np.linspace(xyRange[2], xyRange[3], zMat.shape[0])
xx,yy = np.meshgrid(x,y)
zMax = np.max(zMat)
yMax, xMax = np.where(zMat==zMax)[0][0], np.where(zMat==zMax)[1][0]
levels = np.arange(0,100,1)
showText = "time = {:.1f} s\nhotpoint = {:.1f} C".format(tNow, zMax)
plt.plot(x[xMax],y[yMax],'ro') # 绘制最高温度点
plt.contourf(xx, yy, zMat, 100, cmap=plt.cm.get_cmap('jet'), origin='lower', levels = levels)
plt.annotate(showText, xy=(x[xMax],y[yMax]), xytext=(x[xMax],y[yMax]),fontsize=10)
plt.colorbar()
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Temperature distribution of the plate')
plt.show()
# 模型参数
uIni = 25 # 初始温度值
uBound = 25.0 # 边界条件
c = 1.0 # 热传导参数
qv = 50.0 # 热源功率
x_0, y0 = 0.0, 3.0 # 热源初始位置
vx, vy = 2.0, 1.0 # 热源移动速度
# 求解范围
tc, te = 0.0, 5.0 # 时间范围,0<t<te
xa, xb = 0.0, 16.0 # 空间范围,xa<x<xb
ya, yb = 0.0, 12.0 # 空间范围,ya<y<yb
# 初始化
dt = 0.002 # 时间步长
dx = dy = 0.1 # 空间步长
tNodes = round(te/dt) # t轴 时序网格数
xNodes = round((xb-xa)/dx) # $\mathrm{x}$轴 空间网格数
yNodes = round((yb-ya)/dy) # $\mathrm{y}$轴 空间网格数
xyRange = np.array([xa, xb, ya, yb])
xZone = np.linspace(xa, xb, xNodes+1) # 建立空间网格
yZone = np.linspace(ya, yb, yNodes+1) # 建立空间网格
xx,yy = np.meshgrid(xZone, yZone) # 生成网格点的坐标 xx,yy (二维数组)
# 计算 差分系数矩阵 A、B (三对角对称矩阵),差分系数 rx,ry,ft
A = (-2) * np.eye(xNodes+1, k=0) + (1) * np.eye(xNodes+1, k=-1) + (1) * np.eye(xNodes+1, k=1)
B = (-2) * np.eye(yNodes+1, k=0) + (1) * np.eye(yNodes+1, k=-1) + (1) * np.eye(yNodes+1, k=1)
rx, ry, ft = c*dt/(dx*dx), c*dt/(dy*dy), qv*dt
# 计算 初始值
U = uIni * np.ones((yNodes+1, xNodes+1)) # 初始温度 u0
# 前向Euler 法一阶差分求解
for k in range(tNodes+1):
t = k * dt # 当前时间
# 热源条件
# (1) 恒定热源:Qv(x_0,y0,t) = qv, 功率、位置 恒定
# Qv = qv
# (2) 热源功率随时间变化 Qv(x_0,y0,t)=f(t)
# Qv = qv*np.sin(t*np.pi) if t<2.0 else qv
# (3) 热源位置随时间变化 Qv(x,y,t)=f(x(t),y(t))
xt, yt = x_0+vx*t, y0+vy*t # 热源位置变化
Qv = qv * np.exp(-((xx-xt)**2+(yy-yt)**2)) # 热源方程
# 边界条件
U[:,0] = U[:,-1] = uBound
U[0,:] = U[-1,:] = uBound
# 差分求解
U = U + rx * np.dot(U,A) + ry * np.dot(B,U) + Qv*dt
if k % 100 == 0:
print('t={:.2f}s\tTmax={:.1f} Tmin={:.1f}'.format(t, np.max(U), np.min(U)))
showcontourf(U, xyRange, k*dt) # 绘制等温云图
这段代码只需要把showcontourf放在循环体内即可实现动画效果,可以清晰看到热源在空间中的分布。我这里展示最后状态下的温度分布图:
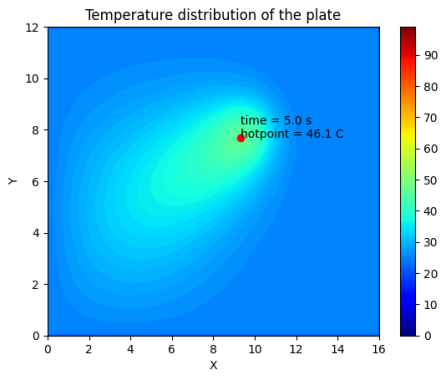
热点周围的温度梯度平滑,这表明热量通过平板均匀扩散。这样的模拟在许多应用中都很有用,例如在散热器设计、理解制造过程中的热梯度,甚至在诸如地热源传播热量的自然现象中。
例2.15 椭圆偏微分方程是一类重要的偏微分方程,主要用来描述物理的平衡稳定状态,如定常状态下的电磁场、引力场和反应扩散现象等,广泛应用于流体力学、弹性力学、电磁学、几何学和变分法中。 考虑如下二维 Poisson 方程:
$$ \frac{ \partial^{2} u }{ \partial x^{2} } + \frac{ \partial^{2} u }{ \partial y^{2} } = f(x,y), \tag{2.3.21}
$$ 这个方程怎么解呢?考虑二维椭圆偏微分方程的数值解法,采用有限差分法求解。简单地,采用五点差分格式表示二阶导数的差分表达式,将上述的偏微分方程离散为差分方程:
$$ \frac{u{i-1,j}+u{i+1,j} - 2u{i,j}}{(\Delta x)^{2}} + \frac{u{i,j-1}+u{i,j+1} - 2u{i,j}}{(\Delta y)^{2}} = f(x{i}, y{j}), \tag{2.3.22}
$$ 椭圆型偏微分描述不随时间变化的均衡状态,没有初始条件,因此不能沿时间步长递推求解。对上式的差分方程,可以通过矩阵求逆方法求解,但当$h$较小时网格很多,矩阵求逆的内存占用和计算量极大。于是,可以使用迭代松弛法递推求得二维椭圆方程的数值解。假定$x$和$y$的间距都为$h$,松弛系数为$w$,则迭代过程可以表示为:
$$ u{i,j}^{k+1} \leftarrow (1-w)u{i,j}^{k} + \frac{w}{4} \Big[ u{i,j+1}^{k} + u{i,j-1}^{k} + u{i+1,j}^{k} + u{i-1,j}^{k} - h^{2}f(x{i},x{j}) \Big], \tag{2.3.23}
$$ 考虑一个特殊情况,也就是当$f(x,y)=0$的情况下,迭代松弛法的代码如下:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 求解范围
xa, xb = 0.0, 1.0 # 空间范围,xa<x<xb
ya, yb = 0.0, 1.0 # 空间范围,ya<y<yb
# 初始化
h = 0.01 # 空间步长, dx = dy = 0.01
w = 0.5 # 松弛因子
nodes = round((xb-xa)/h) # $\mathrm{x}$轴 空间网格数
# 边值条件
u = np.zeros((nodes+1, nodes+1))
for i in range(nodes+1):
u[i, 0] = 1.0 + np.sin(0.5*(i-50)/np.pi)
u[i, -1] = -1.0 + 0.5*np.sin((i-50)/np.pi)
u[0, i] = -1.0 + 0.5*np.sin((i-50)/np.pi)
u[-1, i] = 1.0 + np.sin(0.5*(50-i)/np.pi)
# 迭代松弛法求解
for iter in range(100):
for i in range(1, nodes):
for j in range(1, nodes):
u[i, j] = w/4 * (u[i-1, j] + u[i+1, j] + u[i, j-1] + u[i, j+1]) + (1-w) * u[i, j]
# 绘图
x = np.linspace(0, 1, nodes+1)
y = np.linspace(0, 1, nodes+1)
xx, yy = np.meshgrid(x, y)
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(xx, yy, u, cmap=plt.get_cmap('rainbow'))
fig.colorbar(surf, shrink=0.5)
ax.set_xlim3d(0, 1.0)
ax.set_ylim3d(0, 1.0)
ax.set_zlim3d(-2, 2.5)
ax.set_title("2D elliptic partial differential equation")
ax.set_xlabel("X")
ax.set_ylabel("Y")
plt.show()

sympy中的pdsolve给出了一些简单偏微分方程的解析解法,但sympy目前不支持二阶偏微分方程的求解。pdsolve的调用格式形如pdsolve(eq, func=None, hint='default', dict=False, solvefun=None, **kwargs),具体使用我们可以看到下面的例子:
例2.16 使用sympy中的pdsolve解下面这个偏微分方程:
$$ -2 \frac{ \partial f }{ \partial x } + 4 \frac{ \partial f }{ \partial y } + 5f = e^{x+3y}, \tag{2.3.24}
$$ 可以给出如下代码:
from sympy.solvers.pde import pdsolve
from sympy import Function, pprint, exp
from sympy.abc import x,y
f = Function('f')
eq = -2*f(x,y).diff(x) + 4*f(x,y).diff(y) + 5*f(x,y) - exp(x + 3*y)
pdsolve(eq)
给出的结果为:
Eq(f(x, y), (F(4*x + 2*y)*exp(x/2) + exp(x + 4*y)/15)*exp(-y))
2.4 微分方程的应用案例
在本节中,我们将探讨微分方程在现实世界中的应用,特别是在工业和日常生活中的一些实例。通过这些案例,我们可以加深对微分方程建模过程的理解。
2.4.1 人口增长的两种经典模型—— Malthus 模型和 Logistic 模型
人口增长是微分方程建模的一个经典例子。我们可能在高中生物课上已经接触过指数增长(J型曲线)和 Logistic 增长(S型曲线),但可能没有深入了解它们的计算方法和曲线的具体特性。实际上,这些曲线可以通过微分方程来描述。不仅生物种群的增长遵循这些规律,人口增长也是如此。
最简单的模型是 Malthus 模型,它假定人口增长率是一个恒定的常数,因此每年的人口增加量与当年的人口总数成正比:
$$ \frac{\mathrm{d}x}{\mathrm{d}t} = rx, \quad x(t{0}) = x{0}. \tag{2.4.1}
$$ 即使不用Python,我们也可以轻松手动求解这个微分方程:
$$ x(t) = x{0}e^{r(t-t{0})}, \tag{2.4.2}
$$ 其中,增长率$r$是一个恒定的值。这个模型的假设包括:
- 忽略死亡率对人口增长的影响,只考虑净增长率
- 忽略人口迁移对问题的影响,只关注自然增长
- 忽略重大突发事件对人口的突变性影响
- 忽略人口增长率变化的滞后性
然而,仔细想一想,无论是人还是动物,增长率怎么可能持续不变地指数增长呢?如果一直稳步增长,地球很快就会人满为患。实际上,增长率会受到许多外部因素的影响,比如食物供应、天敌、疾病等突发事件,甚至种群内部的竞争也会降低增长率。那么,这个模型是否完全没有解释价值呢?并非如此,至少在没有天敌、疾病且食物充足的时期,物种的增长确实接近指数增长。一个典型的例子是澳大利亚的野兔。
因此,我们可以对增长率进行一些调整:假设某个地区的人口存在一个最大承载量$x_{m}$(也就是我们以前接触到的$K$值),随着人口增长,增长率呈线性下降。这样,原始的 Malthus 模型就被修正为:
$$ \frac{\mathrm{d}x}{\mathrm{d}t} = r \left( 1 - \frac{x}{x{m}} \right), \quad x(t{0}) = x_{0}. \tag{2.4.3}
$$ 该模型被称为 Logistic 模型。事实上,这个方程可以求解出解析解,并且如果绘制它的曲线,会呈现出S形。方程的解析解为:
$$ x(t) = \frac{x{m}}{\displaystyle 1 + \left( \frac{x{m}}{x{0}} - 1 \right) e^{-r(t-t{0})}}. \tag{2.4.4}
$$
注意:这两个模型都是人口预测中的经典模型,需要重点掌握。然而,这两个模型都是从宏观角度出发,没有考虑诸如人口结构、人口迁移等更微观的因素。此外,这些模型对数据量的要求并不高,如果数据量太大,可能需要使用时间序列方法进行分析。
接下来,我们可以通过一个例子来进一步了解这些模型。
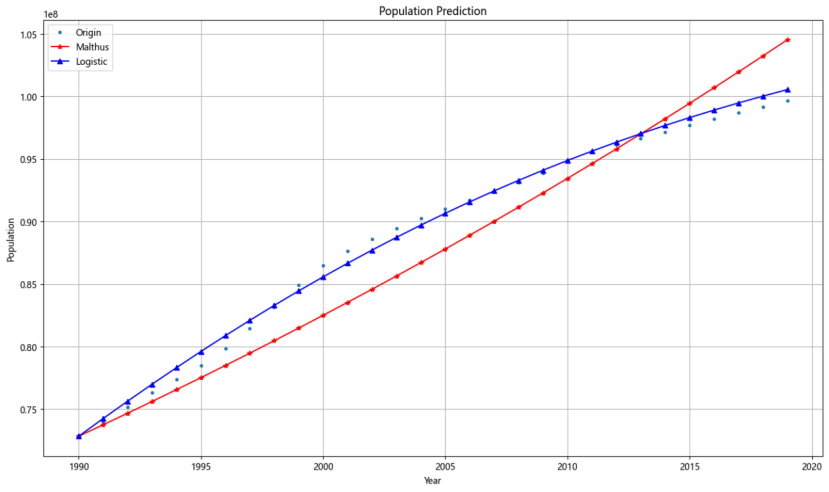
例3.7 假设我们有某地1980年至2010年间的人口变化数据,我们想比较 Malthus 模型和 Logistic 模型对人口变化的拟合效果,并预测2011年的人口数据。假设数据已经存储在文件中,我们可以将其读取并保存到变量中进行分析。
import pandas as pd
import numpy as np
from scipy import optimize
data=pd.read_excel("总人口.xls")
data1=data[['年份','年末总人口(万人)']].values
y=data['年末总人口(万人)'].values.astype(float)
x_0=y[0]
#Logistic
def f2(x,r,K):
return K/(1+(K/x_0-1)*np.exp(-r*x))
#Malthus
def f(x,r):
return x_0*np.exp(r*x)
x=np.arange(0,30,1)
x_00=np.arange(1990,2020,1)
plt.figure(figsize=(16,9))
plt.grid()
fita,fitb=optimize.curve_fit(f,x,y)
print(fita)
plt.plot(x_00,10000*y,'.')
x1=f(x,fita[0])
plt.plot(x_00,10000*x1,'r*-')
fita,fitb=optimize.curve_fit(f2,x,y)
print(fita)
x1=f2(x,0.0578,11019)
plt.plot(x_00,10000*x1,'b^-')
plt.legend(["Origin","Malthus","Logistic"])
plt.xlabel("Year")
plt.ylabel("Population")
plt.title('Population Prediction')
plt.show()
最终可以画出模型的拟合图,如图2.4.1所示。
2.4.2 波浪能受力系统
本节内容改编自2022年全国大学生数学建模竞赛A题。
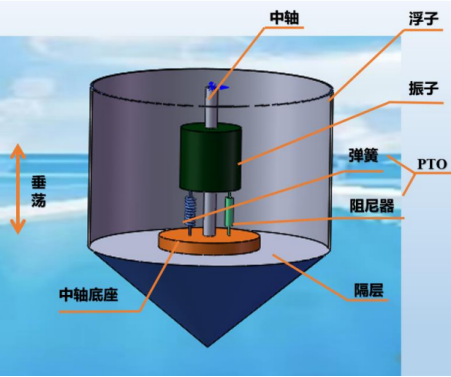
随着社会的进步和经济的增长,对绿色能源技术的需求日益增加。波浪能,作为一种清洁的可再生能源,具有巨大的潜力和广阔的发展前景。波浪能的有效利用是能源技术研究的重要方向之一。一个典型的波浪能装置由浮标、振荡器、中心轴和能量转换系统(PTO,包括弹簧和阻尼器)组成。在这种装置中,振荡器、中心轴和PTO被封装在浮标内部。当浮标受到周期性波浪的作用时,它会受到波浪激励力、附加质量力、波浪阻尼力和静水复原力等多种力的影响。
- 假设浮标和振荡器仅在垂直方向上进行一维振动。计算在波浪激励力作用下,前40个波浪周期内,每隔0.2秒浮标和振荡器的垂直位移和速度。
- 若考虑浮标和振荡器不仅有一维振动,还有平面内的摆动。此时,波浪的输入除了提供振动的波浪激励力外,还会提供一个用于摆动的波浪激励力矩。此外,除了直线阻尼器,转轴上还安装有旋转阻尼器和扭转弹簧,这些元件共同输出能量。计算在波浪激励力和波浪激励力矩作用下,前40个波浪周期内,每隔0.2秒浮标与振荡器的垂直位移和速度以及纵摇角位移和角速度。
这是一个动力学系统建模问题。对于浮标和振荡器组成的整体系统,其受到的外力包括浮力、波浪激励力、波浪阻尼力和附加质量力的综合作用,这些力共同决定了浮标和振荡器系统的加速度。而浮力与系统的重力之间的差值实际上就是静水复原力。对于振荡器来说,其受到的力仅包括重力、阻尼力和弹簧力。在初始状态下,由于系统处于静止状态,初始阻尼力为零,弹簧力与振荡器的重力相平衡。在运动过程中,这三种力的合力提供了合加速度。通过求解二阶微分方程组,我们可以模拟整个动力学过程。对于不同的阻尼系数,我们只需进行分类讨论即可。相比于问题一,问题二考虑了转动问题。为了研究方便,我们将运动分解为沿轴方向的垂直振动和平面内的纵摇摆动。纵摇和垂直振动的方程实际上非常相似,本质上是外力矩提供了振荡器和浮标的角速度。
在平衡状态下,如果将浮标和振荡器视为一个整体系统,系统的浮力与两者的重力相平衡。在系统内部,弹簧力和阻尼器的阻尼力作为系统的内力。但由于在平衡状态下浮标和振荡器的相对速度为零,因此阻尼器不提供阻尼力。在这种状态下,弹簧力与振荡器的重力平衡,阻尼器由于速度差为零而不提供阻尼力。根据胡克定律,我们可以得到:
$$ mg - kl_{0} = 0. \tag{2.4.5}
$$
带入$k=80000\text{ N/m}$,我们可以得到初始弹簧的初始压缩量$l_{0}$为$0.2980\text{ m}$。 在初始状态下,由于浮力与系统的重力平衡,根据阿基米德原理,浮力等于排出的液体重力,我们可以得到:
$$ \rho gV_{0} = (m+M)g. \tag{2.4.6}
$$
解得初始平衡状态下浮标浸没在水面下的体积为$7.1210$立方米。已知浮标的几何参数,我们可以求解其浸没在水面下的深度。经过计算,锥体部分的体积为$0.8378$立方米,而柱体部分半径为$1$米,解得柱体浸没在水面下的深度为$2$米,加上锥体高度$0.8$米,因此整体浸没在水面下的高度为$2.8$米。
如果想让系统进入垂直振动状态,需要给浮标一个初始速度或加速度。波浪为系统提供动力,但由于波浪在提供动力的同时也为周围的海水提供动能,海水反过来作用于浮标,因此产生了附加质量力。所以,附加质量力的作用对象是海水,它与浮标一起以相同的加速度运动。在运动过程中,我们取竖直向上为正方向,浮标和振荡器的位移分别为和\。对于振荡器来说,其受力始终只包括弹簧力、阻尼力和自身的重力。根据 Newton第二定律,我们可以得到振荡器的运动方程:
$$ k(l{0} + x{1} - x{2}) + \eta \left( \frac{\mathrm{d}x{1}}{\mathrm{d}t} - \frac{\mathrm{d}x{2}}{\mathrm{d}t{2}} \right) - mg = m \frac{\mathrm{d}^{2}x_{2}}{\mathrm{d}t^{2}}. \tag{2.4.8}
$$ 在初始状态下,振子的速度和加速度均为零。同时,由于初始状态下振子的重力与弹簧的弹力处于平衡状态,我们可以简化相关的方程为:
$$ k(x{1} - x{2}) + \eta \left( \frac{\mathrm{d}x{1}}{\mathrm{d}t} - \frac{\mathrm{d}x{2}}{\mathrm{d}t{2}} \right)= m \frac{\mathrm{d}^{2}x{2}}{\mathrm{d}t^{2}}. \tag{2.4.9}
$$ 考虑将振子和浮子作为一个整体系统,阻尼器提供的阻尼力与弹簧的弹力构成系统的内力。根据 Newton第二定律,系统的外力包括波浪提供的激励力、兴波阻尼力、系统受到的浮力以及系统的重力。同时,考虑到虚拟质量对浮子产生的惯性力,我们在计算加速度时需要将虚拟质量考虑在内。因此,系统的合力决定了浮子、振子以及虚拟质量的加速度:
$$ \rho g V + f \cos (\omega t) - \psi \frac{\mathrm{d}x{1}}{\mathrm{d}t} - (m + M)g = (M + m{0}) \frac{\mathrm{d}^{2}x{1}}{\mathrm{d} t^{2}} + m \frac{\mathrm{d}^{2}x{2}}{\mathrm{d} t^{2}}. \tag{2.4.9}
$$ 由于初始平衡状态下浮力与系统重力相互抵消,因此在运动状态中,浮力与重力的差值即静水恢复力等于浸没在水下的体积变化所对应的重力:
$$ \rho g V - (m + M) g = \rho g \int{d}^{x{1}} \pi z^{2}(h) \, \mathrm d{h}. \tag{2.4.10}
$$ 那么,方程(7)可以简化为:
$$ \rho g \int{d}^{x{1}} {\pi z^{2}(h)} \, \mathrm d{h} + f \cos (wt) - \psi \frac{\mathrm{d}x{1}}{\mathrm{d}t} = (M + m{0}) \frac{\mathrm{d}^{2}x{1}}{\mathrm{d} t^{2}} + m \frac{\mathrm{d}^{2}x{2}}{\mathrm{d}t^{2}}. \tag{2.4.11}
$$ 而对于下面两种不同的情况,阻尼器的阻尼系数不同。
情形一:阻尼器的阻尼系数为常数:
$$ \eta = 10000. \tag{2.4.12}
$$
情形二:阻尼器的阻尼系数与速度差的绝对值有关,幂指数为$0.5$:
$$ \eta = 1000 \left[ \frac{\mathrm{d}x{1}}{\mathrm{d}t} - \frac{\mathrm{d}x{2}}{\mathrm{d}t} \right]^{0.5}. \tag{2.4.13}
$$
给出代码实现如下:
import numpy as np
from matplotlib import rcParams
from math import *
from sympy.abc import t
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def pfun_1(ip,t):
"""第1小问微分方程模型"""
x,y,z,w=ip
return np.array([z,
w,
(-k*(x-y)-beta*(z-w))/m2,
(k*(x-y)+beta*(z-w)+f*cos(omega*t)-gama*y-Ita*w)/(m1+m_d)
])
def pfun_2(ip,t):
"""第2小问微分方程模型"""
x,y,z,w=ip
return np.array([z,
w,
(-k*(x-y)-beta*sqrt(abs(z-w))*(z-w))/m2,
(k*(x-y)+beta*sqrt(abs(z-w))*(z-w)+f*cos(omega*t)-gama*y-Ita*w)/(m1+m_d)
])
if __name__=='__main__':
dt=0.01
m1=4866#浮子质量
m2=2433#振子质量
m_d=1335.535#垂荡附加质量 (kg)
k=80000#弹簧刚度 (N/m)
beta=10000#平动阻尼系数
f=6250#垂荡激励力振幅 (N)
omega=1.4005#入射波浪频率 (s-1)
T_max=(2*pi/omega)*40#模拟最大时间
gama=1025*9.8*pi#静水恢复力系数
Ita=656.3616#垂荡兴波阻尼系数 (N·s/m)
t_lst=np.arange(0,T_max,dt)
pfun=pfun_2#选择计算第1小问还是第2小问
sol=odeint(pfun,[0.0,0.0,0.0,0.0],t_lst)
rcParams['font.sans-serif']=['SimHei']
plt.figure()
plt.plot(t_lst,sol[:,0],label='振子位移')
plt.plot(t_lst,sol[:,1],label='浮子位移')
plt.legend()
plt.figure()
plt.plot(t_lst,sol[:,2],label='振子速度')
plt.plot(t_lst,sol[:,3],label='浮子速度')
plt.legend()
得到结果如图所示:
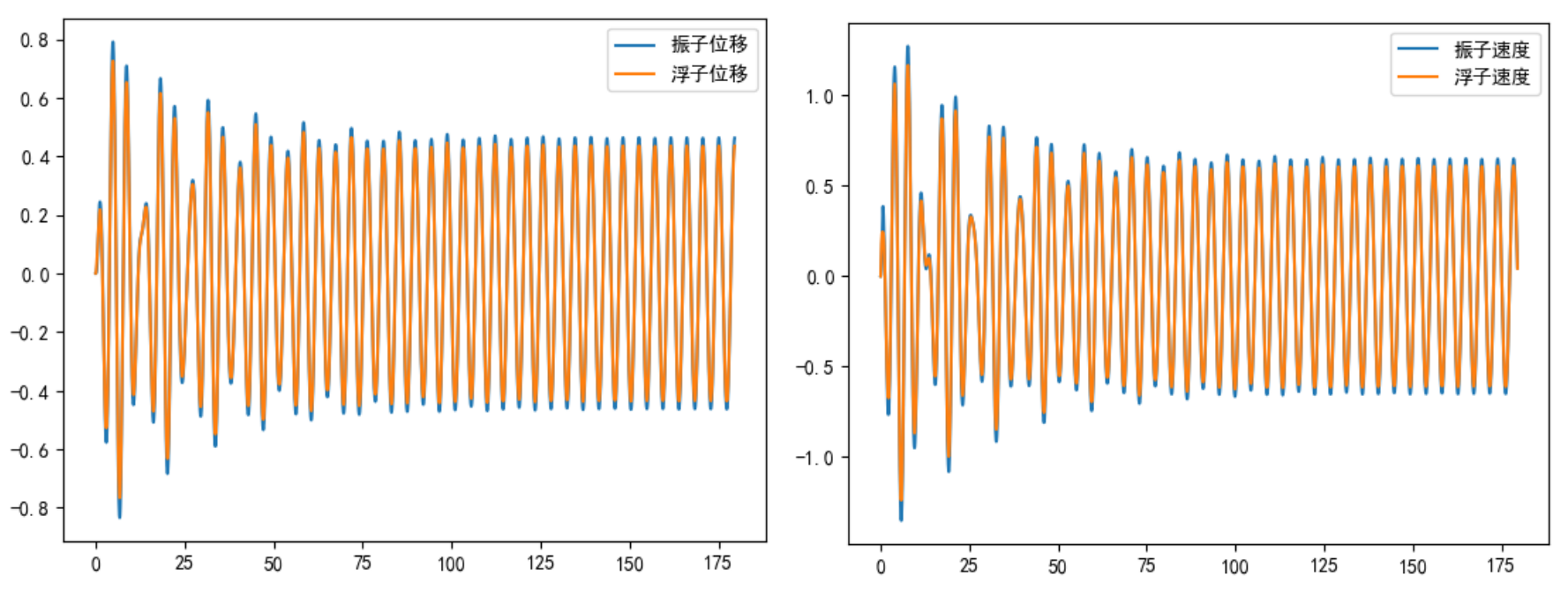
系统的摇荡过程包括沿自身轴线的垂荡运动和在一个平面内的纵摇运动。系统各部分在运动过程中受到的力如图2.4.4所示:
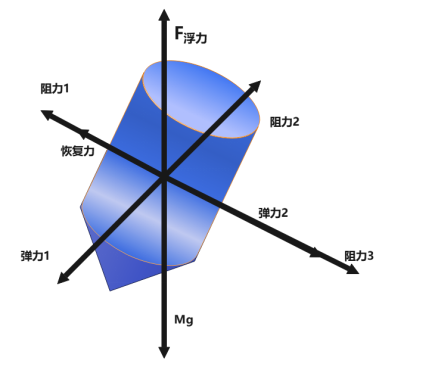
$$ k(l{0} + x{1} - x{2}) + \eta \left[ \frac{\mathrm{d}x{1}}{\mathrm{d}t} - \frac{\mathrm{d}x{2}}{\mathrm{d}t} \right]+ mg (1 - \cos \theta{2}) = m \frac{\mathrm{d}^{2}x_{2}}{\mathrm{d}t^{2}}, \tag{2.4.14}
$$ 对于纵摇方向上的运动,重力在垂直于杆的方向上提供了力矩,加上弹簧的扭矩和旋转阻尼力矩,我们可以得到一个基于角动量定理的表达式:
$$ K(\theta2 - \theta{1}) + \lambda \left[ \frac{\mathrm{d}\theta{2}}{\mathrm{d}t} - \frac{\mathrm{d}\theta{1}}{\mathrm{d}t} \right] - mgL{2} \sin \theta{2} = J{2} \frac{\mathrm{d}^{2}\theta{2}}{\mathrm{\mathrm{d}t^{2}}}. \tag{2.4.15}
$$ 对于由浮子和振子构成的系统,垂荡运动的表达式类似于问题一:
$$ \begin{align} &\rho gV \cos \theta{1} + f \cos (\omega t) - \psi \frac{\mathrm{d}x{1}}{\mathrm{d}t} - (mg \cos \theta{2} + MgL{1}\cos \theta{1}) \&= (M + m{0}) \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}} + m \frac{\mathrm{d}^{2}x_{2}}{\mathrm{d}t^{2}}. \end{align} \tag{2.4.16}
$$ 在海水中进行纵摇运动时,静水恢复力矩可以使浮体转正,其大小与浮体相对于静水面的转角成正比,比例系数称为静水恢复力矩系数。因此,我们假设静水恢复力矩、总体重力力矩和浮力力矩的矢量和为零:
$$ \rho g V x{1} \sin \theta{1} - (mgL{2} \sin \theta{2} + MgL{1} \sin \theta{1}) = \varepsilon \theta_{1}, \tag{2.4.17}
$$ 其中$\varepsilon$为静水恢复力矩系数。在纵摇方向上,浮力和重力在垂直于竖直方向上提供力矩,加上外部的波浪激励力矩和兴波阻尼力矩:
$$ \varepsilon \theta{1} + L \cos(\omega t) - \phi \frac{\mathrm{d}\theta{1}}{\mathrm{d}t} = (J{1} + J{0}) \frac{\mathrm{d}^{2}\theta{1}}{\mathrm{d}t^{2}} + J{2} \frac{\mathrm{d}^{2}\theta_{2}}{\mathrm{d}t}. \tag{2.4.18}
$$ 实现这个模型的代码如下:
import numpy as np
from matplotlib import rcParams
from math import *
from sympy.abc import t
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def pfun(ip,t):
"""第3问微分方程模型"""
x,y,z,w,th1,th2,ph1,ph2=ip
A=np.array([[1,0,0,0,0,0,0,0],
[0,1,0,0,0,0,0,0],
[0,0,m_v,m_v*cos(th2),0,0,0,0],
[0,0,0,m_f+m_d,0,0,0,0],
[0,0,0,0,1,0,0,0],
[0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,J_f+J_d,0],
[0,0,0,-m_v*(l0+x+0.5*h_v)*sin(th2),0,0,0,J_v+m_v*(l0+x+0.5*h_v)**2]])
b=np.array([[z],
[w],
[m_v*g*(1-cos(th2))+m_v*(l0+x+0.5*h_v)*ph2**2-k1*x-beta_1*z],
[m_v*g*(1-cos(th2))+(k1*x+beta_1*z)*cos(th2)+f*cos(omega*t)-Ita_1*w-gama_1*y],
[ph1],
[ph2],
[k2*(th2-th1)+beta_2*(ph2-ph1)-Ita_2*ph1-(((2+15*(2-y)**2)/(8+30*(2-y)))*((m_v+m_f)*g-1025*g*pi*y)+gama_2)*th1+L*cos(omega*t)],
[m_v*g*(l0+x+0.5*h_v)*sin(th2)-2*z*ph2*m_v*(l0+x+0.5*h_v)-k2*(th2-th1)-beta_2*(ph2-ph1)]])
Op=np.dot(np.linalg.inv(A),b)
return Op.reshape((-1,))
if __name__=='__main__':
dt=0.01
g=9.8
l0=0.2019575#弹簧初始长度
m_f=4866#浮子质量
m_v=2433#振子质量
m_d=1028.876#垂荡附加质量 (kg)
J_d=7001.914#纵摇附加转动惯量 (kg·m^2)
J_v=202.75#振子绕质心转动惯量
J_f=16137.73119#浮子转动惯量
k1=80000#弹簧刚度 (N/m)
k2=250000#扭转弹簧刚度 (N·m)
beta_1=10000#直线阻尼器阻尼系数
beta_2=1000#旋转阻尼器阻尼系数
f=3640#垂荡激励力振幅 (N)
L=1690#纵摇激励力矩振幅 (N·m)
omega=1.7152#入射波浪频率 (s-1)
T_max=(2*pi/omega)*40#模拟最大时间
gama_1=1025*g*pi#静水恢复力系数
gama_2=8890.7#静水恢复力矩系数 (N·m)
Ita_1=683.4558#垂荡兴波阻尼系数 (N·s/m)
Ita_2=654.3383#纵摇兴波阻尼系数 (N·m·s)
h_v=0.5#振子高度
t_lst=np.arange(0,T_max,dt)
sol=odeint(pfun,[0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0],t_lst)
"""将振子相对铰链中心的径向位移、速度转换成垂荡位移、垂荡速度"""
xx=np.zeros(sol.shape[0])
vx=np.zeros(sol.shape[0])
for idx in range(xx.shape[0]):
xx[idx]=(l0+sol[idx,0])*cos(sol[idx,5])-l0+sol[idx,1]
vx[idx]=sol[idx,2]*cos(sol[idx,5])+sol[idx,3]
rcParams['font.sans-serif']=['SimHei']
plt.figure()
plt.title('')
plt.plot(t_lst,xx,label='振子垂荡位移')
plt.plot(t_lst,sol[:,1],label='浮子垂荡位移')
plt.legend()
plt.figure()
plt.plot(t_lst,vx,label='振子垂荡速度')
plt.plot(t_lst,sol[:,3],label='浮子垂荡速度')
plt.legend()
plt.figure()
plt.plot(t_lst,sol[:,4],label='浮子纵摇角度')
plt.plot(t_lst,sol[:,5],label='振子纵摇角度')
plt.legend()
plt.figure()
plt.plot(t_lst,sol[:,6],label='浮子纵摇角速度')
plt.plot(t_lst,sol[:,7],label='振子纵摇角速度')
plt.legend()
得到结果图像如图所示:
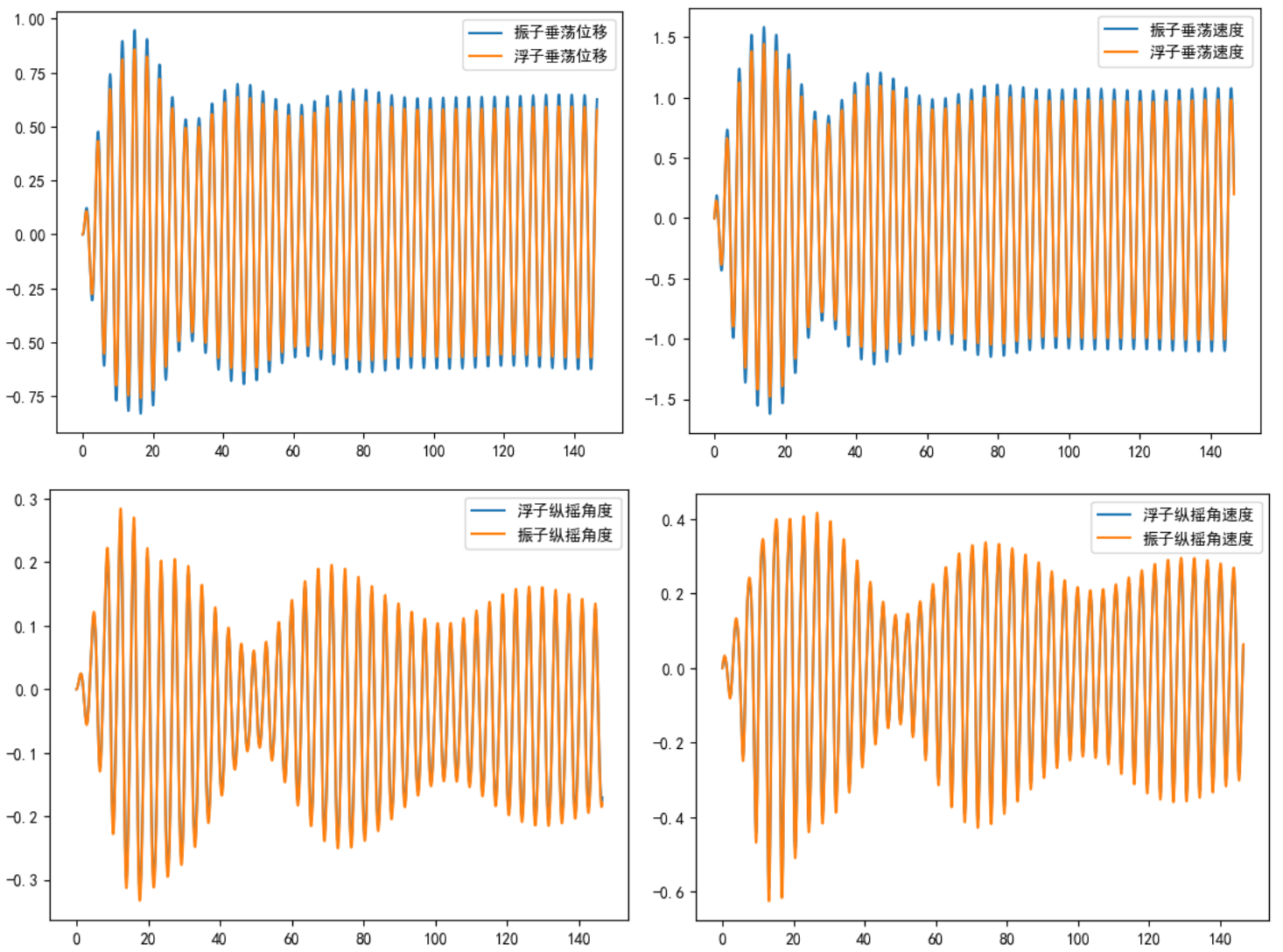
值得注意的是,类似于问题一,图13展示了振子和浮子质心高度随时间的变化曲线。初始状态以平衡态浮子的锥顶高度作为$0$高度基准,而位移表示的是相对变化量。因此,在实际求解过程中,需要减去初始高度。
如图2.4.5右上子图所示,振子和浮子的速度变化情况可以观察到,浮子的运动速度变化范围大于振子,其上下速度波动范围介于$-1.5$至$1.5$米/秒。尽管速度差异不显著,但可以看出振子的速度有时会超过$1.5$米/秒,而浮子的速度则不会超过这一值。因此,尽管两者的速度波形相似,但仍存在一定的波动和相位差。
在分析纵摇运动时,我们也考察了振子和浮子的转动情况。以竖直方向作为平衡位置,若开始时两者均以逆时针方向运动,并以此方向为正方向定义,则物体的纵摇运动和垂荡运动构成了一个整体,不能单独对纵摇或垂荡进行分析,因为重力的分量不同,且这一分量的变化是周期性的。
从图2.4.5中可以看出,在初始阶段,浮子的纵摇角速度会突然增加,而振子的增加速度相对缓慢。这是因为海浪给予的初始力矩较大,使浮子获得了较大的角加速度。在模拟过程中,由于$t=0.2$秒这一时间间隔可能略长,导致模拟的速度在初始阶段增长非常快。浮子通过旋转压缩弹簧和阻尼器,提供的弹力迫使振子和浮子保持相同的旋转方向运动。
通过求解,我们得到了几个重要时间节点的垂荡运动和纵摇运动情况,如表2所示。
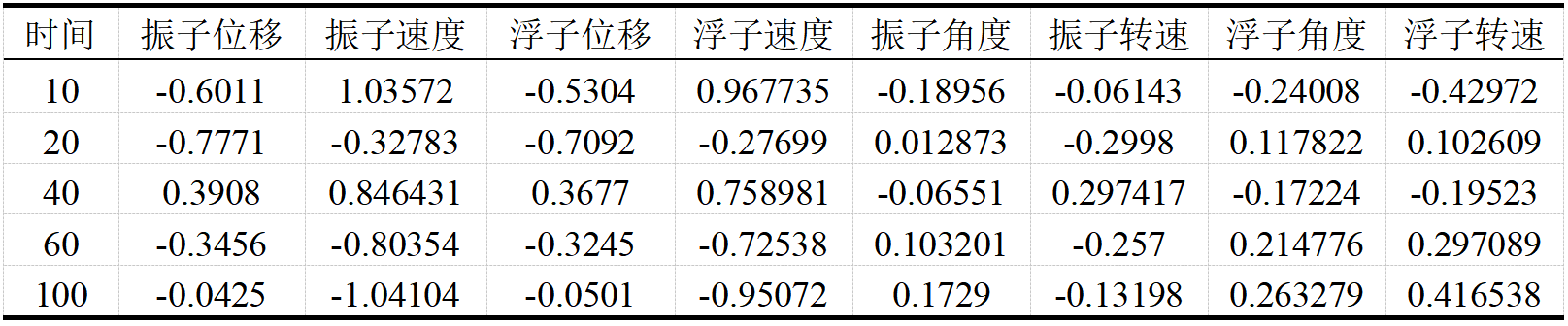
2.4.3 新冠病毒的传播模型—— SI、SIS、SIR、SEIR模型
自2020年起,新冠疫情的爆发彻底打乱了我们的日常生活。在这场全球性的疫情中,不仅医院的医生和科研人员在前线奋斗,许多互联网公司也开发了健康码和行程码来帮助防疫。此外,高校的数学研究者和学生们也发挥了重要作用,他们通过数学建模来预测和分析新冠病毒的传播趋势,比如英国的帝国理工学院、中国的西安交通大学和武汉大学等。
为了有效控制疫情,模型需要能够预测病毒在不同阶段的传播情况。新冠病毒传播迅速,感染周期短,变异速度快,这使得疫苗研发面临巨大挑战。因此,我们需要考虑易感人群、无症状感染者和已感染者之间的动态平衡。
在编写代码时,只需明确传染速率和恢复速率以及人员流动情况即可。可以将人群分为绿码、黄码和红码三种状态,这种分类具有以下特点:
- 传播速度快,影响范围广,但可以连续变化。
- 绿码、黄码、红码人群的比例总和为1。
- 绿码减少的数量等于黄码增加的数量,黄码减少的数量等于红码增加的数量,红码康复的数量等于绿码增加的数量,即总体保持平衡
SI模型是一种简单的传播模型,将人群分为易感者(S类)和感染者(I类)两类。通过SI模型,我们可以预测疫情高峰的到来。通过提高卫生标准和加强防控措施,可以延缓疫情高峰的出现。
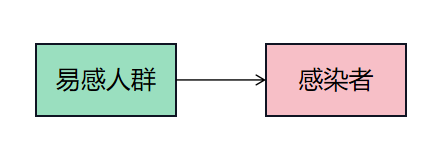
数学模型为
$$ \begin{align} N \frac{\mathrm{d}i(t)}{\mathrm{d}t} &= \lambda N s(t) i(t), \[0.5em] s(t) + i(t) &= 1. \end{align} \tag{2.4.19}
$$ 你可能已经注意到,这实际上是一个 Logistic 模型。如果尝试编程解决这个模型,最终结果会是一条S型曲线,即所有人最终都会被感染。这个结论显然不合理,说明模型中还有一些未考虑到的因素。
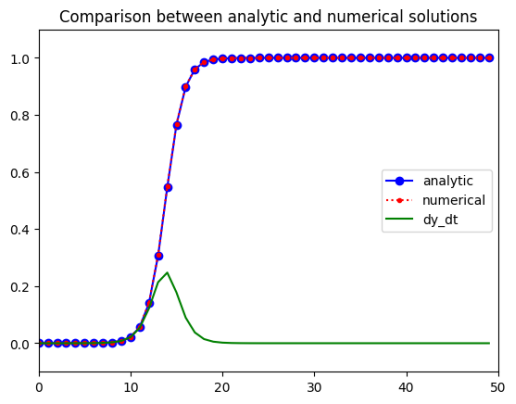
SI模型的仿真代码如下。
# 设置模型参数
lamda = 1.0 # 日接触率, 患病者每天有效接触的易感者的平均人数
y0 = 1e-6 # 患病者比例的初值
tEnd = 50 # 预测日期长度
t = np.arange(0.0,tEnd,1) # (start,stop,step)
def dy_dt(y, t): # 定义导数函数 f(y,t)
dy_dt = lamda*y*(1-y) # di/dt = lamda*i*(1-i)
return dy_dt
yAnaly = 1/(1+(1/i0-1)*np.exp(-lamda*t)) # 微分方程的解析解
yInteg = odeint(dy_dt, y0, t) # 求解微分方程初值问题
yDeriv = lamda * yInteg *(1-yInteg)
# 绘图
plt.plot(t, yAnaly, '-ob', label='analytic')
plt.plot(t, yInteg, ':.r', label='numerical')
plt.plot(t, yDeriv, '-g', label='dy_dt')
plt.title("Comparison between analytic and numerical solutions")
plt.legend(loc='right')
plt.axis([0, 50, -0.1, 1.1])
plt.show()
SI模型的仿真结果如图2.4.7所示。
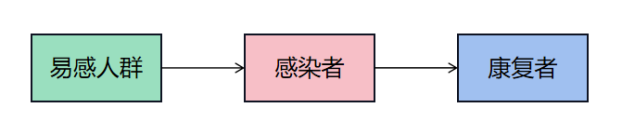
$$ \begin{align} N \frac{\mathrm{d}s}{\mathrm{d}t} &= -N \lambda si, \[0.5em] N \frac{\mathrm{d}i}{\mathrm{t}} &= N\lambda si - N \mu i, \[0.5em] s(t) + i(t) + r(t) &= 1. \end{align} \tag{2.4.20}
$$
SIR模型的仿真代码如下。
def dySIR(y, t, lamda, mu): # SIR 模型,导数函数
i, s = y
di_dt = lamda*s*i - mu*i # di/dt = lamda*s*i-mu*i
ds_dt = -lamda*s*i # ds/dt = -lamda*s*i
return [di_dt,ds_dt]
# 设置模型参数
lamda = 0.2 # 日接触率, 患病者每天有效接触的易感者的平均人数
sigma = 2.5 # 传染期接触数
mu = lamda/sigma # 日治愈率, 每天被治愈的患病者人数占患病者总数的比例
fsig = 1-1/sigma
tEnd = 200 # 预测日期长度
t = np.arange(0.0,tEnd,1) # (start,stop,step)
i0 = 1e-6 # 患病者比例的初值
s0 = 1-i0 # 易感者比例的初值
Y0 = (i0, s0) # 微分方程组的初值
print("lamda={}\tmu={}\tsigma={}\t(1-1/sig)={}".format(lamda,mu,sigma,fsig))
ySIR = odeint(dySIR, Y0, t, args=(lamda,mu)) # SIR 模型
# 绘图
#plt.title("Comparison among SI, SIS and SIR models")
plt.xlabel('t')
plt.axis([0, tEnd, -0.1, 1.1])
plt.axhline(y=0,ls="--",c='c') # 添加水平直线
plt.plot(t, ySIR[:,0], '-r', label='i(t)-SIR')
plt.plot(t, ySIR[:,1], '-b', label='s(t)-SIR')
plt.plot(t, 1-ySIR[:,0]-ySIR[:,1], '-m', label='r(t)-SIR')
plt.legend(loc='best') # youcans
plt.show()
SIR模型的仿真结果如图2.4.9所示。
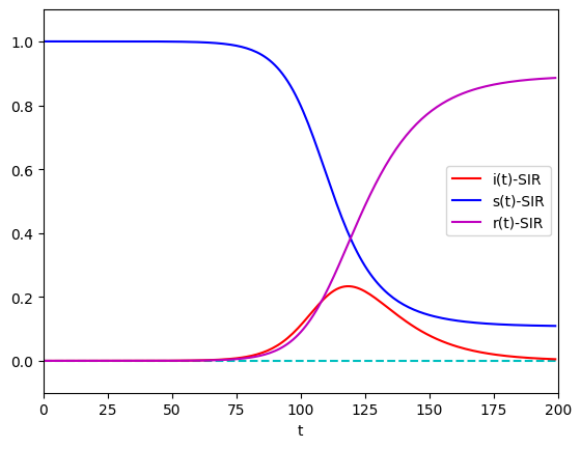

$$ \begin{align} N \frac{\mathrm{d}s}{\mathrm{d}t} &= -N \lambda si, \[0.5em] N \frac{\mathrm{d}e}{\mathrm{d}t} &= N \lambda si - N \delta e, \[0.5em] N \frac{\mathrm{d}i}{\mathrm{d}t} &= N \delta e - N \mu i, \[0.5em] N \frac{\mathrm{d}r}{\mathrm{d}t} &= -N \mu si, \[0.5em] s(t) + e(t) + i(t) + r(t) &= 1. \end{align} \tag{2.4.21}
$$
注意:为了使模型更加全面,我们可以考虑加入更多的转变路径。比如,康复者可能由于病毒的变异重新变成易感个体;或者易感个体通过接种疫苗而直接获得免疫,成为康复者。这些补充路径让模型更加精细,更贴近于COVID-19的实际传播模式,为我们预测疾病的转折点提供了工具。
SEIR模型的仿真代码如下。
def dySEIR(y, t, lamda, delta, mu): # SEIR 模型,导数函数
s, e, i = y # youcans
ds_dt = -lamda*s*i # ds/dt = -lamda*s*i
de_dt = lamda*s*i - delta*e # de/dt = lamda*s*i - delta*e
di_dt = delta*e - mu*i # di/dt = delta*e - mu*i
return np.array([ds_dt,de_dt,di_dt])
# 设置模型参数
lamda = 0.3 # 日接触率, 患病者每天有效接触的易感者的平均人数
delta = 0.03 # 日发病率,每天发病成为患病者的潜伏者占潜伏者总数的比例
mu = 0.06 # 日治愈率, 每天治愈的患病者人数占患病者总数的比例
sigma = lamda / mu # 传染期接触数
fsig = 1-1/sigma
tEnd = 300 # 预测日期长度
t = np.arange(0.0,tEnd,1) # (start,stop,step)
i0 = 1e-3 # 患病者比例的初值
e0 = 1e-3 # 潜伏者比例的初值
s0 = 1-i0 # 易感者比例的初值
Y0 = (s0, e0, i0) # 微分方程组的初值
# odeint 数值解,求解微分方程初值问题
ySEIR = odeint(dySEIR, Y0, t, args=(lamda,delta,mu)) # SEIR 模型
# 输出绘图
print("lamda={}\tmu={}\tsigma={}\t(1-1/sig)={}".format(lamda,mu,sigma,fsig))
plt.title("Comparison among SI, SIS, SIR and SEIR models")
plt.xlabel('t')
plt.axis([0, tEnd, -0.1, 1.1])
plt.plot(t, ySEIR[:,0], '--', color='r', label='s(t)-SEIR')
plt.plot(t, ySEIR[:,1], '-.', color='g', label='e(t)-SEIR')
plt.plot(t, ySEIR[:,2], '-', color='b', label='i(t)-SEIR')
plt.plot(t, 1-ySEIR[:,0]-ySEIR[:,1]-ySEIR[:,2], ':', color='k', label='r(t)-SEIR')
plt.legend(loc='right') # youcans
plt.show()
SEIR模型的仿真结果如图2.4.11所示。
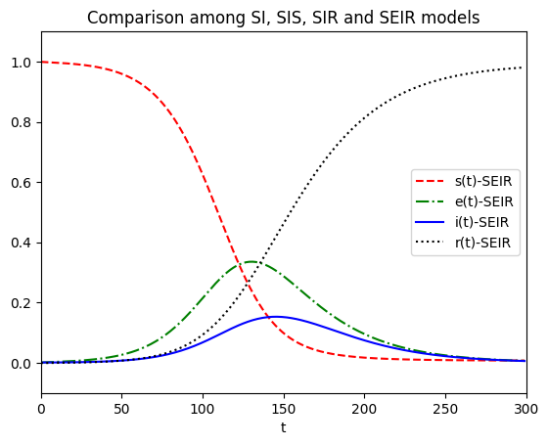
2.4.4 被捕食者-捕食者模型 —— Volterra 模型
考虑一个关于森林中狼和羊共存的扩展模型。在这个模型中,狼是捕食者,羊是食草动物。我们之前已经讨论了 Logistic 生长模型,现在我们将进一步考虑不同物种之间的相互影响。 假设羊有充足的食物资源,如果没有狼的捕食,羊的数量将按照Malthus模型以固定的增长率r1呈指数增长。然而,由于狼的捕食,羊的数量会减少,我们假设这种减少的速率与狼和羊的数量成正比:
$$ \begin{align} \frac{\mathrm{d}x{1}}{\mathrm{d}t} &= x{1}(r{1} - \lambda{1}x{2}), \[0.5em] \frac{\mathrm{d}x{2}}{\mathrm{d}t} &= x{2}(r{2} - \lambda{2}x{1}). \end{align}
$$ 可以对这一模型进行仿真模拟,代码如下。
alpha = 1.
beta = 1.
delta = 1.
gamma = 1.
x_0 = 4.
y0 = 2.
def derivative(X, t, alpha, beta, delta, gamma):
x, y = X
dotx = x * (alpha - beta * y)
doty = y * (-delta + gamma * x)
return np.array([dotx, doty]
Nt = 1000
tmax = 30.
t = np.linspace(0.,tmax, Nt)
x_0 = [x_0, y0]
res = odeint(derivative, x_0, t, args = (alpha, beta, delta, gamma))
x, y = res.T
plt.figure(figsize=(16,9))
plt.grid()
plt.title("odeint method")
plt.plot(t, x, 'xb-', label = 'Deer')
plt.plot(t, y, '+r-', label = "Wolves")
plt.xlabel('Time t, [days]')
plt.ylabel('Population')
plt.legend()
plt.show()
plt.figure()
IC = np.linspace(1.0, 6.0, 9) # initial conditions for deer population (prey)
# np.linspace和arange不同,从1.0开始,到6.0结束,均分为9段
for deer in IC:
x_0 = [deer, 1.0]
Xs = odeint(derivative, x_0, t, args = (alpha, beta, delta, gamma))
plt.plot(Xs[:,0], Xs[:,1], "-", label = "$x_0 =$"+str(x_0[0]))
plt.xlabel("Deer")
plt.ylabel("Wolves")
plt.legend()
plt.title("Deer vs Wolves")
plt.show()
得到狼羊的物种数量变化曲线与相轨线,如图2.4.12所示。
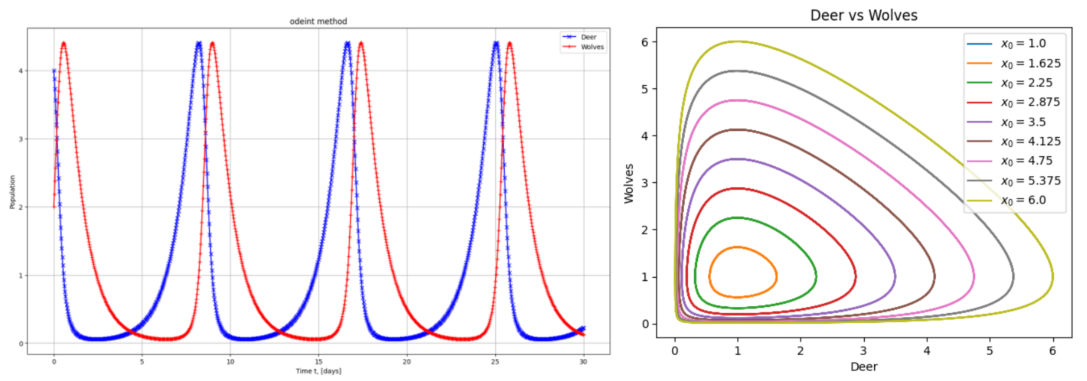
2.5 差分方程的典型案例
接下来,我们讨论差分方程,它与微分方程的关系就像离散与连续的关系。实际上,数列的差分问题本身就可以视为差分方程的一个应用案例。无论是差分方程还是微分方程,它们的某些思想、理论和背景都是相通的。
2.5.1 差分方程与微分方程建模的异同
差分方程可以看作是微分方程的离散形式,其解法通常采用递推方法。值得注意的是,常微分方程的通解方法与相应的差分方程的解法是相似的。微分方程以其简洁的思想和纯粹的条件,通过微元分析,使得建模变得容易,能够处理多变量系统。然而,微分方程的模型相对原始,求解并不总是容易。相比之下,差分方程通过对连续系统的离散化处理,能够考虑更多因素,尽管有时求解同样困难,但在应用上更为广泛。
2.5.2 人口模型的新讨论 —— Leslie模型
以前我们讨论的 Logistic 模型和 Malthus 模型主要关注增长率,没有考虑人口结构、性别比例和人口迁移等因素。Leslie模型则对这些因素进行了考虑和改进。
在正常的社会或自然条件下,生育率和死亡率与群体的年龄结构密切相关。因此,我们需要根据年龄对整个群体进行层次划分,建立与年龄相关的人口模型。Leslie模型是一种基于不同年龄段人群生育率差异的模型,它通过构建变化矩阵进行分析,能够充分考虑种群内的性别比和年龄段差异。 我们将女性人口按年龄等间隔划分为n个年龄组,并将时间离散化,间隔与年龄组相同。假设各个年龄组的生育率b和存活率s不随时间变化,我们可以建立一个模型来描述这种情况。
$$ \left{ \begin{align} f{i}(t+1) &= \sum\limits{i=1}^{n} b{i}f{i}(t), \[0.5em] f{i+1}(t+1) &= s{i}f_{i}(t). \end{align} \right. \tag{2.5.1}
$$ 其中$i=1,2,...,n-1$。 在式(2.5.1)中,假设中已扣除了在t时段以后出生而活不到t+1时段的婴儿,记Leslie矩阵:
$$ \boldsymbol{L} = \left[ \begin{matrix} b{1} & b{2} & \cdots & b{n}\ s{1} & 0 & \cdots & 0\ 0 & s{2} & \cdots & 0\ \vdots & \vdots & \ddots & \vdots\ 0 & 0 & \cdots & s{n} \end{matrix} \right], \tag{2.5.2}
$$ 记$\boldsymbol f(t)=[f{1}(t),f{2}(t),...,f_{n}(t)]^{\top}$,则式(3.31)可以写作:
$$ \boldsymbol{f}(t+1) = \boldsymbol{Lf}(t). \tag{2.5.3}
$$ 通过计算 Leslie 矩阵$\boldsymbol{L}$并使用初始的人口分布向量$\boldsymbol f(0)$,我们能够预测任何给定时刻$t$的女性人口分布$\boldsymbol f(t)$。然后,将这些预测值除以女性在总人口中的比例,就可以得到全国总人口$N(t)$在时刻$t$的估计值。
利用2021年的人口统计数据,我们可以对中国未来一段时间内的人口变化进行预测。在此,要感谢华中科技大学电信学院2020级的邓立桐同学,他协助我们从国家统计年鉴中获取了所需的数据,并进行了相关仿真分析。仿真结果显示了全国人口总数以及不同年龄段人口比例的预期变化趋势,如图2.5.1所示。
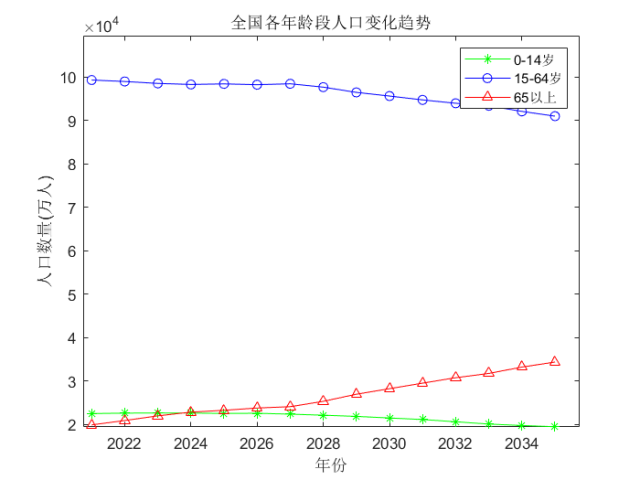
注意:模拟仿真用数据可以从国家统计局和人口年鉴中查找。
图2.5.1展示了经过模拟仿真得到的人口变化趋势。需要注意的是,这些仿真数据可以从国家统计局和人口年鉴中获得。从图中我们可以看出,在实施三胎政策之后,未来十五年内,15至64岁的人口数量及其在总人口中的比重仍将继续减少,老龄化问题依旧难以得到有效缓解。预计到2035年,65岁及以上的人口将占总人口的$23.7\%$。这一趋势反映了当前人口老龄化已经相当严重,加之生活压力较大,放宽生育政策对于不愿生育的人群和只有一个孩子的家庭影响有限,主要对有两个孩子的家庭产生一定影响。
仿真代码如下:
import pandas as pd
import numpy as np
a=pd.read_excel("data3.xlsx")
p=0.48764
N00=a['总人口(万人)']
N00=np.array(N00)
A=np.eye(90)
b=a['生存率'][0:90]
b1=b/100
for i in range(90):
A[i,:]*=b1[i]
c=a['调节后生育率'][0:90]
c1=c/1000
M=sum(c1)
d=np.zeros((91,1))
B=np.vstack([c1,A])
L=np.hstack([B,d])
G=[]
K=[]
S1=[]
S2=[]
S3=[]
for i in range(1,13):
L0=np.power(L,i)
X=N00@L0
G.append(X)
Z=X/p
K.append(sum(Z))
S1.append(sum(Z[0:15]))
S2.append(sum(Z[15:65]))
S3.append(sum(Z[65:-1]))
K=np.array(K)
S1=np.array(S1)
S2=np.array(S2)
S3=np.array(S3)
x=range(2023,2035)
y1=S1/K
y2=S2/K
y3=S3/K
plt.figure(2)
plt.plot(x,y1,'-or')
plt.plot(x,y2,'-ob')
plt.plot(x,y3,'-og')
plt.title('我国全国各年龄段人口变化趋势')
plt.xlabel('时间(单位:年)')
plt.ylabel('人口数量(单位:万人)')
plt.legend(['年龄在0-14岁总人数','年龄在15-64岁总人数','年龄在65及65岁以上总人数'])
plt.show()
另外,补充一个有趣的小事,这个问题正是笔者在2021年冬季为笔者学校数学建模校赛所命制的F题,2022年夏季的中青杯也考的几乎一模一样。
2.6 元胞自动机与仿真模拟
在之前的讨论中,我们主要关注了如何针对连续问题建立函数和微分方程模型进行求解。对于一些离散问题,我们尝试使用了差分方程模型。然而,差分方程模型往往难以有效地模拟大多数离散模型。因此,我们将介绍一种强大的工具——元胞自动机。
2.6.1 元胞自动机的理论
元胞自动机是一种具有时间、空间和状态离散性的网格动力学模型,其中空间相互作用和时间因果关系局部化。它能够模拟复杂系统的时空演化过程。元胞自动机的一个显著特点是它不依赖于固定的数学公式。因此,在数学建模中,有一个俗语:“遇到难题时,就用元胞自动机”。
自从元胞自动机被提出以来,对其分类的研究成为了一个重要的研究课题和核心理论。根据不同的角度和标准,元胞自动机可以有多种分类方式。1990年,Howard A. Gutowitz 提出了一种基于元胞自动机行为的马尔可夫概率测量的层次化、参数化分类体系。S. Wolfram 对一维元胞自动机的演化行为进行了详细分析,并在大量计算机实验的基础上,将所有元胞自动机的动力学行为归纳为四大类:
- 平稳(Stable):从任何初始状态开始,经过一定时间运行后,元胞空间趋于一个空间平稳的构形。这里的空间平稳指的是每个元胞都处于固定状态,不随时间变化,例如规则254;
- 周期(Periodic):经过一定时间运行后,元胞空间趋于一系列简单的固定结构或周期结构。这些结构可以被视为一种滤波器,因此可用于图像处理研究,例如规则90;
- 混沌(Chaos):从任何初始状态开始,经过一定时间运行后,元胞自动机表现出混沌的非周期行为。所生成的结构的统计特征保持不变,通常表现为分形维特征,例如规则110;
- 复杂(Complex):出现复杂的局部结构,或者说是局部的混沌,其中有些会不断地传播,例如规则30。
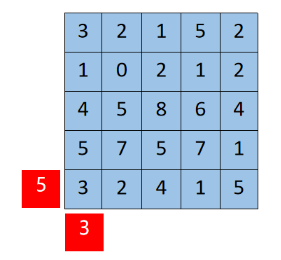
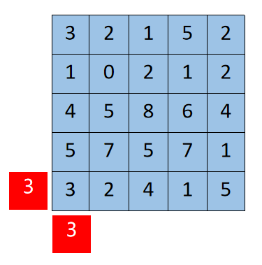
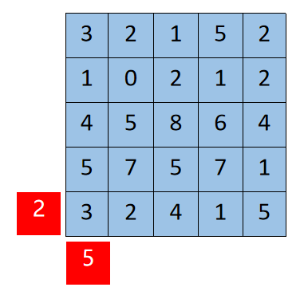
理论上,元胞空间应该是无限的,但实际上这是不可能的。因此,我们需要像处理偏微分方程一样为其添加一些“邻居”,即所谓的边界条件。 对于固定型边界,我们在扩展边界时将扩展值设置为相同的常数值,如图所示:

2.6.2 元胞自动机的应用——生命游戏
生命游戏(Game of Life)是由英国数学家约翰·康威(John Horton Conway)于1970年发明的一种元胞自动机。它是一个零玩家游戏,意味着游戏的演化是由初始状态决定的,不需要玩家的进一步输入。生命游戏的规则非常简单,但它能够产生极其复杂的行为,被誉为“元胞自动机的代表作”。生命游戏的规则如下:
- (Exposure)当前细胞为存活状态时,当周围的存活细胞低于2个时(不包含2个),该细胞变成死亡状态
- (Survive)当前细胞为存活状态时,当周围有2个或3个存活细胞时,该细胞保持原样
- (Overcrowding)当前细胞为存活状态时,当周围有超过3个存活细胞时,该细胞变成死亡状态
- (Reproduction)当前细胞为死亡状态时,当周围有3个存活细胞时,该细胞变成存活状态
尽管规则简单,生命游戏却能够展示出类似于生物系统中的复杂行为,如细胞的出生、死亡和繁衍。它不仅在数学和计算机科学中被广泛研究,还成为了人工生命和复杂系统理论的一个重要模型。
生命游戏的一个有趣特点是,它能够产生各种各样的图案,包括静态图案、振荡图案和移动图案(如滑翔机)。这些图案的演化可以被看作是计算过程的一种形式,因此生命游戏也被认为是一种基本的计算模型。
下面的Python代码示例展示了如何使用NumPy和Matplotlib库来模拟生命游戏。该示例包括创建初始随机网格、添加滑翔机图案以及实现环形边界条件的功能。通过调整参数和初始条件,可以探索生命游戏中各种有趣的行为和图案。
## eg.1.
import sys,argparse #argparse是python的一个命令行解析包
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.colors import ListedColormap
yeah =('purple','yellow')
cmap = ListedColormap(yeah)
ON = 255
OFF = 0
vals = [ON, OFF]
def randomGrid(N):
"""returns a grid of NxN random values"""
return np.random.choice(vals, N*N, p=[0.2, 0.8]).reshape(N, N) #采用随机的初始状态
def addGlider(i, j, grid):
"""adds a glider with top-left cell at (i, j)"""
glider = np.array([[0, 0, 255],
[255, 0, 255],
[0, 255, 255]])
# 3×3 的 numpy 数组定义了滑翔机图案(看上去是一种在网格中平稳穿越的图案)。
grid[i:i+3, j:j+3] = glider
#可以看到如何用 numpy 的切片操作,将这种图案数组复制到模拟的二维网格中
# 它的左上角放在 i和 j指定的坐标,即用这个方法在网格的特定行和列增加一个图案,
#实现环形边界条件
def update(frameNum, img, grid, N):
newGrid = grid.copy()
for i in range(N):
for j in range(N):
total = int((grid[i, (j-1)%N] + grid[i, (j+1)%N] +
grid[(i-1)%N, j] + grid[(i+1)%N, j] +
grid[(i-1)%N, (j-1)%N] + grid[(i-1)%N, (j+1)%N] +
grid[(i+1)%N, (j-1)%N] + grid[(i+1)%N, (j+1)%N])/255)
# 因为需要检测网格的 8个边缘。更简洁的方式是用取模(%)运算符
# 可以用这个运算符让值在边缘折返
# Conway实现规则 :生命游戏的规则基于相邻细胞的 ON 或 OFF 数目
# 为了简化这些规则的应用,可以计算出处于 ON 状态的相邻细胞总数。
if grid[i, j] == ON:
if (total < 2) or (total > 3):
newGrid[i, j] = OFF
else:
if total == 3:
newGrid[i, j] = ON
# update data
img.set_data(newGrid)
grid[:] = newGrid[:]
return img,
#向程序发送命令行参数,mian()
def main():
# command line arguments are in sys.argv[1], sys.argv[2], ...
# sys.argv[0] is the script name and can be ignored
# parse arguments
parser = argparse.ArgumentParser(description="Runs Conway's Game of Life simulation.")
# add arguments
parser.add_argument('--grid-size', dest='N', required=False) #定义了可选参数,指定模拟网格大小N
parser.add_argument('--mov-file', dest='movfile', required=False) #指定保存.mov 文件的名称
parser.add_argument('--interval', dest='interval', required=False) #设置动画更新间隔的毫秒数
parser.add_argument('--glider', action='store_true', required=False) #用滑翔机图案开始模拟
parser.add_argument('--gosper', action='store_true', required=False)
args = parser.parse_args()
#初始化模拟
# set grid size
N = 100
if args.N and int(args.N) > 8:
N = int(args.N)
# set animation update interval
updateInterval = 50
if args.interval:
updateInterval = int(args.interval)
# declare grid
grid = np.array([])
# check if "glider" demo flag is specified,设置初始条件,要么是默认的随机图案,要么是滑翔机图案。
if args.glider:
grid = np.zeros(N*N).reshape(N, N) #创建 N×N 的零值数组,
addGlider(1, 1, grid) #调用 addGlider()方法,初始化带有滑翔机图案的网格
else:
# populate grid with random on/off - more off than on
grid = randomGrid(N)
# 设置动画
fig, ax = plt.subplots(facecolor='pink') #配置 matplotlib 的绘图和动画参数
img = ax.imshow(grid,cmap=cmap, interpolation='nearest') #用plt.show()方法将这个矩阵的值显示为图像,并给 interpolation 选项传入'nearest'值,以得到尖锐的边缘(否则是模糊的)
ani = animation.FuncAnimation(fig, update, fargs=(img, grid, N, ),#animation.FuncAnimation()调用函数 update(),该函数在前面的程序中定义,根据 Conway 生命游戏的规则,采用环形边界条件来更新网格。
frames=10,
interval=updateInterval,
save_count=50)
# number of frames?
# set the output file
if args.movfile:
ani.save(args.movfile, fps=30, extra_args=['-vcodec', 'libx264'])
plt.show()
# call main
if __name__ == '__main__':
main()
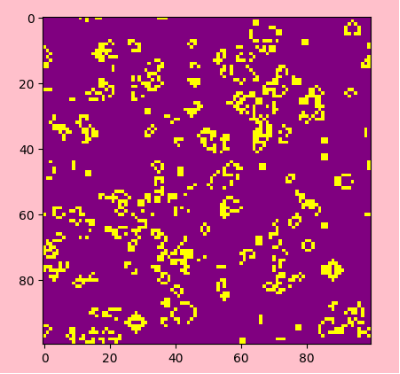
2.6.3 元胞自动机的应用 —— 森林山火扩散模型
在此小节中,我们利用元胞自动机模拟了森林火灾的扩散过程。通过建立一个简单的模型,我们能够观察火势如何在森林中蔓延,以及如何受到植被分布、环境因素和偶发事件(如闪电)的影响。本模型的基本假设包括:
- 空地(黑色)、树木(绿色)、火焰(红色)三种状态;
- 绿色树木可以因相邻的火焰而燃烧;
- 空地上有一定的概率生长出新的树木;
- 闪电可以随机引燃树木。
通过设定不同的参数,如树木密度、燃烧概率、生长率和闪电概率,我们可以模拟出多种火灾情景。该模拟为理解火灾的动力学和预防措施提供了一个直观的平台。代码执行后,展示了500个模拟步骤,每一步都在更新显示火灾蔓延的状态。模拟的动态演示不仅可以帮助研究人员理解和预测真实世界中的火灾行为,也可用于教育和展示目的,以提高公众对森林火灾危险性的认识。
在本节的代码中,我们使用numpy和matplotlib库来创建并迭代森林的状态,numpy用于高效的矩阵计算,而matplotlib则用于可视化每一步的结果。森林的每个单元格都可以根据邻居的状态和随机事件来更新其状态,从而产生一个动态且引人入胜的模拟过程。
import numpy as np#科学计算库 处理多维数据(矩阵)
import matplotlib.pyplot as plt#绘图工具库
import matplotlib as mpl
#设置基本参数
global Row,Col#定义全局变量行和列
Row=100#行
Col=100#列
forest_area=0.8#初始化这个地方是树木的概率
firing=0.8#绿树受到周围树木引燃的概率
grow=0.001#空地上生长出树木的概率
lightning=0.00006#闪电引燃绿树的概率
forest=(np.random.rand(Row,Col)<forest_area).astype(np.int8)
#初始化作图
plt.title("step=1",fontdict={"family":'Times New Roman',"weight":'bold',"fontsize":20})#字体,加粗,字号
colors=[(0,0,0),(0,1,0),(1,0,0)]#黑色空地 绿色树 红色火
bounds=[0,1,2,3]#类数组,单调递增的边界序列
cmap=mpl.colors.ListedColormap(colors)#从颜色列表生成颜色的映射对象
w=plt.imshow(forest,cmap=cmap,norm=mpl.colors.BoundaryNorm(bounds,cmap.N))
#迭代
T=500#迭代500次
for t in range(T):
temp=forest#上一个状态的森林
temp=np.where(forest==2,0,temp)#燃烧的树变成空地
p0=np.random.rand(Row,Col)#空位变成树木的概率
temp=np.where((forest==0)*(p0<grow),1,temp)#如果这个地方是空位,满足长成绿树的条件,那就变成绿树
fire=(forest==2).astype(np.int8)#找到燃烧的树木
firepad=np.pad(fire,(1,1),'wrap')#上下边界,左右边界相连接
numfire=firepad[0:-2,1:-1]+firepad[2:,1:-1]+firepad[1:-1,0:-2]+firepad[1:-1,2:]
p21=np.random.rand(Row,Col)#绿树因为引燃而变成燃烧的树
p22=np.random.rand(Row,Col)#绿树因为闪电而变成燃烧的树
#Temp = np.where((forest == 1)&(((numfire>0)&(rule1prob<firing))|((numfire==0)&(rule3prob<lightning))),2,Temp)
temp=np.where( (forest==1)&( ( (numfire>0)&(p21<firing) ) | ((numfire==0)&(p22<lightning) ) ) ,2,temp)
forest=temp#更新森林的状态
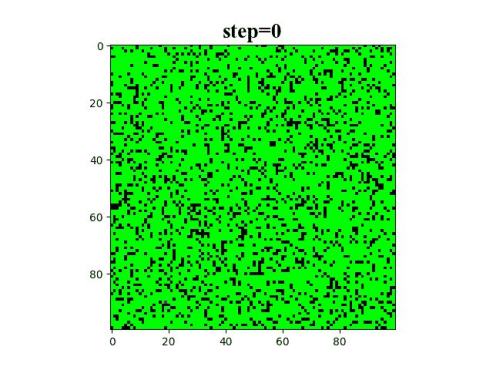
plt.title("step="+str(t),fontdict={"family":'Times New Roman',"weight":'bold',"fontsize":20})#字体,加粗,字号
w.set_data(forest)
plt.pause(0.1)
plt.show()
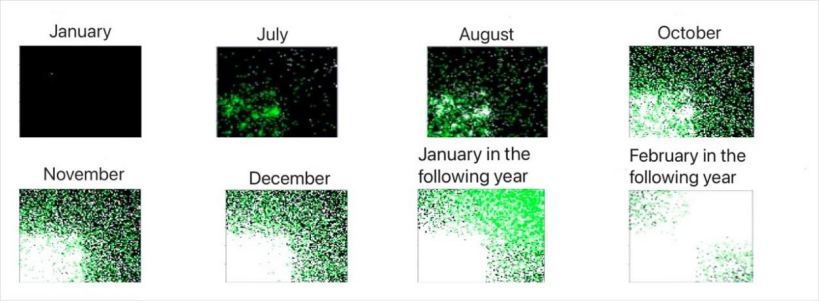
2.6.4 元胞自动机的应用——蒲公英的生长
在本节中,我们使用元胞自动机模型来探索蒲公英的生长模式,以及各种环境因素如何影响其生存和扩散。
- 年度温度波动:温度受多种因素影响,包括纬度、地形以及靠近水体的距离等。然而,在特定地点,年平均温度和最高最低温差已确定的情况下,温度变化主要由季节变化决定。数据分析表明,特定月份的温度可以通过在年平均温度上加上一个正弦波函数来确定。 $$ \text{Temp} = \text{Temp_Avg} + \text{Temp_Diff} \cdot \cos \left( 2\pi \cdot \frac{\text{time}}{12} \right). \tag{2.6.1} $$
- 日照时长的年度变化:与受天气条件影响的日照时长不同,日照主要由季节决定。由于地球围绕太阳的周期性运动,各季节的日出和日落时间不同。日照时长用基础时长表示,即平均时长,并加上一个正弦波函数。 $$ \text{Light} = \text{Daylight_Avg} + \text{Daylight_Diff} \cdot \cos \left( 2\pi \cdot \frac{\text{time}}{12} \right) . \tag{2.6.2} $$
- 降水和风:由于降水和风受到水体近程、温度、山脉存在、海流以及彼此相互影响等多种因素的影响,它们很难预测。然而,降水和风条件存在年度模式。因此,我们编制了三组数据集,每组包含12个元素,代表特定月份的平均降水和风条件。
蒲公英种群和可用养分通过以下公式计算:
$$ \begin{align} \text{Fertility}(t + \Delta t) &= \text{Fertility}(t) + \text{Area} \cdot \text{Repletion_Con} \cdot \text{Rain} \&~ ~ ~ ~- \text{Population_Adult} \cdot \text{Comsumption_Rate_Adult} \&~ ~ ~ ~- \text{Population_Seed} \cdot \text{Comsumption_Rate_Seed}. \end{align} \tag{2.6.3}
$$
- 生育力:土地中的总养分。最初,土地含有一定量的养分。
- 面积:土地的总面积。它与养分恢复率成正比,因为大块土地含有更多有机物和细菌。
- 恢复_常数:该常数用于评估每平方米面积的恢复率。
- 降雨:降雨量与养分恢复率成正比,因为单个细菌在给定时间内消耗一定量的水,并将一定量的有机物分解为养分。因此,能够存活的细菌数量与降雨量成正比。从而,降雨量与养分恢复率成正比。
- 成熟植株消耗率 vs. 种子植株消耗率:成熟植株需要产生种子,这是一个消耗大量能量的过程,而未成熟植株则没有繁殖压力。因此,成熟植株和未成熟植株的养分消耗率不同,应存储在不同的变量中。
解决问题—— 蔓延预测模型建立
蔓延率:考虑一块土地。来自源头$S1$、$S_2$、$S_3$等的种子落在它上面的概率分别是$P{1}$、$P{2}$、$P{3}$等。因此,它不接收到来自源头$S{1}$、$S{2}$、$S{3}$等任何一个种子的概率就是$(1-P{1})$、$(1-P{2})$、$(1-P{3})$等。据此,该土地不接收到任何种子的概率是$(1-P{1}) \cdot (1-P{2}) \cdot (1-P_{3})$等的乘积。
而该土地至少接收到一个种子,从而让蒲公英生长的概率是$1$减去上述概率:$1-(1-P{1}) \cdot (1-P{2}) \cdot (1-P_{3})$等。
在没有风的情况下,蒲公英种子的扩散与距离呈指数关系递减,这是由下式建模的:
$$ \text{Possibility} = \text{Spread_Calm}^{-\text{Distance}}. \tag{2.6.4}
$$ 风的存在能将种子传播。我们假设种子源与风向一致,并以矢量加法简化此过程,其中风被视为一个矢量。因此,特定数量的种子被分布在变化的面积$A = \pi \cdot \text{Distance}^2$上。该可能性由下式建模:
$$ \text{Possibility} = \frac{\text{Spread_Wind}}{\text{Distance}^{2}}. \tag{2.6.5}
$$ 生长率:种子要发育到蒲公英蒴果阶段,需要一定的生长期。在更多养分和有利条件下,未成熟植株可以更快生长。我们创建了变量$K$来确定未成熟植株每月的生长率。 蒲公英生长的最适温度区间能带来最佳结果。然而,在这一区间之外,蒲公英的生长速率呈指数级下降。
$$
\begin{aligned}\
&\rule{200mm}{0.4pt} \
&\textbf{Algorithm 1 蒲公英的生长速率}\[-1.ex]
&\rule{200mm}{0.4pt} \
&\textbf{input} :
\text{Temp}(环境温度)
\
&\textbf{output} :
k\text{Temp}(温度影响的生长速率)
\
&\mathbf{initialize}: T\text{high}(高温阈值),~ T\text{low}(低温阈值),~ \text{Temp_Coeff}(温度参数)
\[-1.ex]
&\rule{200mm}{0.4pt}
\
&\mathbf{if}~ T{\text{high}} > \text{Temp} > T{\text{low}} \
&\hspace{2em} k{\text{Temp}} \leftarrow 1 \
&\mathbf{else~if}~ T{\text{high}} < \text{Temp} \
&\hspace{2em} k{\text{Temp}} \leftarrow \text{Temp_Coeff}^{T{\text{high}} - \text{Temp}} \
&\mathbf{else}\
&\hspace{2em} k{\text{Temp}} \leftarrow \text{Temp_Coeff}^{\text{Temp} - T{\text{low}}} \
&\rule{200mm}{0.4pt} \
&\mathbf{return~}k{\text{Temp}}\
&\rule{200mm}{0.8pt}
\end{aligned}
$$
同样,蒲公英生长的最佳降水也是一个区间。在这个区间之外,生长速率呈指数级下降。
$$
\begin{aligned}\
&\rule{200mm}{0.4pt} \
&\textbf{Algorithm 2 根据降水计算蒲公英的生长速率}\[-1.ex]
&\rule{200mm}{0.4pt} \
&\textbf{input} :
\text{Rain}(环境降水)
\
&\textbf{output} :
k\text{Rain}(降水影响的生长速率)
\
&\mathbf{initialize}: R\text{high}(高降水阈值),~ R\text{low}(低降水阈值),~ \text{Rain_Coeff}(降水参数)
\[-1.ex]
&\rule{200mm}{0.4pt}
\
&\mathbf{if}~ R{\text{Rain}} > \text{Rain} > R{\text{low}} \
&\hspace{2em} k{\text{Temp}} \leftarrow 1 \
&\mathbf{else~if}~ R{\text{high}} < \text{Rain} \
&\hspace{2em} k{\text{Rain}} \leftarrow \text{Rain_Coeff}^{R{\text{high}} - \text{Rain}} \
&\mathbf{else}\
&\hspace{2em} k{\text{Rain}} \leftarrow \text{Rain_Coeff}^{\text{Rain} - R{\text{low}}} \
&\rule{200mm}{0.4pt} \
&\mathbf{return~}k{\text{Rain}}\
&\rule{200mm}{0.8pt}
\end{aligned}
$$
日照对于光合作用至关重要,这意味着蒲公英的生长将随着平均每日日照时数的增加而增加。然而,效果并非线性,因为 $k_\text{Lit}$ 的最大值为:
$$ k_{\text{Lit}} = \frac{\text{Light}}{\text{Light} + \text{Daylight_Coeff}}. \tag{2.6.6}
$$ 生长率($K$)可以使用以下公式计算:
$$ K = k\text{Rain} \cdot k{\text{Temp}} \cdot k_{\text{Lit}} \cdot \left( \frac{\text{Fertility}}{\text{Area}} - \text{Comsumption_Rate_Seed} \right). \tag{2.6.7}
$$ 我们定义蒲公英的起始状态为$0$,结束状态为$1$。每个月,每株蒲公英的生长状态都会增加该月的$K$值。当生长状态超过$1$时,就将其标记为$1$,表示蒲公英已达到蒴果阶段。
死亡率:蒲公英可能因营养不足、极端温度、过多或过少的降雨以及日照不足而死亡。为了评估每月死亡的可能性,我们开发了一个函数。值得注意的是,生长系数与存活系数不同,因为在极端条件下,植物的新陈代谢可以被减缓以提高其生存概率。
$$
\begin{aligned}\
&\rule{200mm}{0.4pt} \
&\textbf{Algorithm 3 计算蒲公英种群的生存率}\[-1.ex]
&\rule{200mm}{0.4pt} \
&\textbf{input} :
\text{Temp}(环境温度),~ \text{Rain}(环境降水)
\
&\textbf{output} :
\text{Survival_Rate_Seed}(幼年体生存率, \text{SS}),~ \text{Survival_Rate_Adult}(成年体生存率, \text{SA})
\
&\mathbf{initialize}: T\text{high}(高温阈值),~ T\text{low}(低温阈值),~ \text{Temp_Coeff}(温度参数), \
&\hspace{5em}R\text{high}(高降水阈值),~ R\text{low}(低降水阈值),~ \text{Rain_Coeff}(降水参数)
\[-1.ex]
&\rule{200mm}{0.4pt}
\
&\mathbf{if}~ T\text{high} > \text{Temp} > T\text{low}: \
&\hspace{2em} k\text{Temp} \leftarrow 1 \
&\mathbf{else~if}~ T\text{high} < \text{Temp}: \
&\hspace{2em} k\text{Temp} \leftarrow \text{Temp_Coeff}^{T\text{high}-\text{Temp}}\
&\mathbf{else}\
&\hspace{2em} k\text{Temp} \leftarrow \text{Temp_Coeff}^{\text{Temp}-T\text{low}} \
\
&\mathbf{if}~ R\text{high} > \text{Rain} > R\text{low}: \
&\hspace{2em} k{\text{Rain}} \leftarrow 1\
&\mathbf{else~if}~ R\text{high} < \text{Rain}:\
&\hspace{2em} k{\text{Rain}} \leftarrow \text{Temp_Coeff}^{R\text{high}-\text{Rain}}\
&\mathbf{else}~ R\text{low} > \text{Rain}:\
&\hspace{2em} k{\text{Rain}} \leftarrow \text{Temp_Coeff}^{\text{Rain}-R\text{low}}\
\
&k{\text{Lit}} \leftarrow \frac{\text{Light}}{\text{Light} + \text{Daylight_Coeff}}\
\
&\text{Survival_Rate_Seed} \leftarrow k{\text{Rain}} \cdot k\text{Temp} \cdot k{\text{Lit}} \cdot \left( \frac{\text{Fertility}}{\text{Area}} - \text{Comsumption_Rate_Seed} \right)\
&\text{Survival_Rate_Adult} \leftarrow k{\text{Rain}} \cdot k\text{Temp} \cdot k{\text{Lit}} \cdot \left( \frac{\text{Fertility}}{\text{Area}} - \text{Comsumption_Rate_Adult} \right)\
&\rule{200mm}{0.4pt} \
&\mathbf{return~}\text{Survival_Rate_Seed},~ \text{Survival_Rate_Adult} \
&\rule{200mm}{0.8pt}
\end{aligned}
$$
每个月,每株未成熟的蒲公英都有一个$\text{SS}$的死亡可能性,而每株成熟的蒲公英有一个$\text{SA}$的死亡可能性。
现在,让我们看一下生成这些图像的代码。代码使用Python编写,通过模拟环境因素如温度、日照、降雨以及风向对蒲公英生长和死亡率的影响来预测蒲公英种群在特定区域的扩散。通过对光合作用、温度和降雨的最佳范围进行建模,这个程序能够模拟蒲公英如何在不同月份内生长并影响土地的肥沃程度。此外,模拟还考虑了成熟植株和种子植株的养分消耗率差异,以及不同生长阶段植株的生存率。这些参数合作模拟了蒲公英如何在一个假设的生态系统中扩散,最终达到一个动态平衡。
import random
import matplotlib.pyplot as plt
#spread factors
Spread_Calm = math.e
Spread_wind = 0.5
#a variable that describe the fertility of land
Fertility = 10000
#a constant that describe rate of repletion per area
Repletion_Con = 0.006
#a constant that describe the rate of energy use of a dandelion
Consumption_rate_Adult = 1
Consumption_rate_Seed = 0.5
#a variable that describe the population of dandelion
population_adult = 0
population_seed = 0
#a constant describe effect of temperature on germination
Temp_Coefficient = 1.125
#a constant describe effect of temperature on survival
Temp_Survival = 1.01
#a constant describe effect of rainfall on germination
Rain_Coefficient = 1.03
#a constant describe effect of rainfall on survival
Rain_Survival = 1.005
#a constant describe effect of daylight on germination
Daylight_Coefficient = 1
#a constant describe effect of daylight on survival
Daylight_Survival = 0.3
#upper limit of optimum temperature
Thigh = 25
#lower limit of optimum temperature
Tlow = 15
#upper limit of optimum rainfall
Rhigh = 200
#lower limit of optimum rainfall
Rlow = 50
#initialize a variable that describe possibility of germination
K = 0
#initialize a variable that describe possibility of survival
SA = 0
SS = 0
#initialize a variable that describe growth rate
Rate = 0
#a constant that describe the size of a single plant in metre
width = 1
#initialize time of a year in month
time = 1
#number of months want to predict
Period = 48
#time counter
Tcounter = 0
#wind factor of west-east wind in each month
W_west_east = [0,0,0,0,0,0,0,0,0,0,0,0]
#wind factor of south-north wind in each month
W_south_north = [0,0,0,0,0,0,0,0,0,0,0,0]
Rainfall = [200,200,200,200,200,200,200,200,200,200,200,200]
Daylight_Avg = 12
Daylight_Diff = 0
Temperature_Avg = 16
Temperature_Diff = 0
def Temperature(Avg,Diff,T):
temperature = Avg - Diff*math.cos(2*(math.pi)*(T/12))
return temperature
def Daylight(Avg,Diff,T):
daylight = Avg - Diff*math.cos(2*(math.pi)*(T/12))
return daylight
def Germination(Tem,Rain,Lit):
k_Tem = 0
k_Rain = 0
k_Lit = 0
if Tem < Tlow:
k_Tem = (Temp_Coefficient)**(Tem-Tlow)
elif Tem > Thigh:
k_Tem = (Temp_Coefficient)**(Thigh-Tem)
else:
k_Tem = 1
if Rain < Rlow:
k_Rain = (Rain_Coefficient)**(Rain-Rlow)
elif Rain > Rhigh:
k_Rain = (Rain_Coefficient)**(Rhigh-Rain)
else:
k_Rain = 1
k_Lit = Lit/(Lit+Daylight_Coefficient)
k = k_Tem*k_Rain*k_Lit*((Fertility/10000)-Consumption_rate_Seed)
return k
def Survival(Tem,Rain,Lit,type):
k_Tem = 0
k_Rain = 0
k_Lit = 0
if Tem < Tlow:
k_Tem = (Temp_Survival)**(Tem-15)
elif Tem > Thigh:
k_Tem = (Temp_Survival)**(25-Tem)
else:
k_Tem = 1
if Rain < Rlow:
k_Rain = (Rain_Survival)**(Rain-Rlow)
elif Rain > Rhigh:
k_Rain = (Rain_Survival)**(Rhigh-Rain)
else:
k_Rain = 1
k_Lit = Lit/(Lit+Daylight_Survival)
if type == 0:
s = k_Tem*k_Rain*k_Lit*((Fertility/10000)-Consumption_rate_Adult)
else:
s = k_Tem*k_Rain*k_Lit*((Fertility/10000)-Consumption_rate_Seed)
return s
#initialize the field
#(0,0,0) represent empty land, (0,255,0) represent seed, (255,255,255) represent dandelion
field = [[(0,0,0) for i in range(int(100/width))] for j in range(int(100/width))]
#initialize the field for growth time
growth_table = [[0 for i in range(int(100/width))] for j in range(int(100/width))]
#set the first dandelion
field[0][0] = (255,255,255)
growth_table[0][0] = 1
for Tcounter in range(Period):
population_adult = 0
population_seed = 0
for Column_index in range(int(100/width)):
for Row_index in range(int(100/width)):
if field[Column_index][Row_index] == (255,255,255):
population_adult = population_adult + 1
if field[Column_index][Row_index] == (0,255,0):
population_seed = population_seed + 1
temp = Temperature(Temperature_Avg,Temperature_Diff,time)
light = Daylight(Daylight_Avg,Daylight_Diff,time)
rain = Rainfall[time-1]
Fertility = Fertility + 10000*Repletion_Con*rain
Fertility = Fertility - population_adult*Consumption_rate_Adult - population_seed*Consumption_rate_Seed
K = Germination(temp,rain,light)
SA = Survival(temp,rain,light,0)
SS = Survival(temp,rain,light,1)
for Column_index in range(int(100/width)):
for Row_index in range(int(100/width)):
if growth_table[Column_index][Row_index] >= 1 and field[Column_index][Row_index] == (0,255,0):
field[Column_index][Row_index] = (255,255,255)
growth_table[Column_index][Row_index] = 1
for Column_index in range(int(100/width)):
for Row_index in range(int(100/width)):
if field[Column_index][Row_index] == (0,0,0):
Spreading = 1
no_seed = 1
for inner_column in range(int(100/width)):
for inner_row in range(int(100/width)):
if field[inner_column][inner_row] == (255,255,255):
Distance = ((Column_index-(inner_column+W_south_north[time-1]))**2+(Row_index-(inner_row+W_west_east[time-1]))**2)**(0.5)
if W_south_north[time-1] != 0 or W_west_east[time-1] != 0:
if Distance == 0:
have_seed = Spread_wind
else:
have_seed = Spread_wind/((Distance)**2)
else:
have_seed = Spread_Calm**(-1*Distance)
no_seed = no_seed*(1-have_seed)
Spreading = 1-no_seed
Possibility_factor = random.random()
if Spreading>=Possibility_factor:
field[Column_index][Row_index] = (0,255,0)
growth_table[Column_index][Row_index] = 0
for Column_index in range(int(100/width)):
for Row_index in range(int(100/width)):
if field[Column_index][Row_index] == (0,255,0):
growth_table[Column_index][Row_index] = growth_table[Column_index][Row_index] + K
for Column_index in range(int(100/width)):
for Row_index in range(int(100/width)):
if field[Column_index][Row_index] == (0,255,0):
Possibility_factor = random.random()
if SS <= Possibility_factor:
field[Column_index][Row_index] = (0,0,0)
growth_table[Column_index][Row_index] = 0
elif field[Column_index][Row_index] == (255,255,255):
Possibility_factor = random.random()
if SA <= Possibility_factor:
field[Column_index][Row_index] = (0,0,0)
growth_table[Column_index][Row_index] = 0
if time <12:
time = time + 1
else:
time = 1
plt.imshow(field)
plt.title('Field')
plt.xlabel('distance/m')
plt.ylabel('distance/m')
plt.show()
2.6.5 元胞自动机的应用——新冠病毒的扩散
在本节中,我们探讨使用元胞自动机模型模拟新冠病毒(COVID-19)的扩散。在这个模型中,每个细胞代表一个人,可以处于以下状态之一:易感者(S0),感染者(S1),治愈者(S2),或潜伏者(S3)。模型中包含以下转换规则:
- 易感者(S0)根据邻近感染者的数量以一定概率变成潜伏者(S3)或直接变成感染者(S1);
- 感染者(S1)具有传播病毒的能力,经过一段时间后自动变成治愈者(S2);
- 治愈者(S2)拥有暂时免疫力,但在本模型中,我们假设治愈者获得永久免疫;
- 潜伏者(S3)在经过一定潜伏期后变成感染者(S1)。
通过这个模型,我们能够模拟和观察疾病如何在人群中传播,以及不同的干预措施如何影响疾病的扩散。例如,可以通过调整感染率、潜伏期和治愈时间的参数来模拟不同的公共卫生策略,如社交距离、戴口罩和隔离措施的效果。此模型为疾病控制决策提供了一个有力的工具,并有助于公共卫生专家和政策制定者更好地理解和应对疫情。
我们使用Python编写了一个简单的模拟程序,其中包括初始化各状态的人群分布、定义状态转换规则以及视觉展示模拟过程。pygame库用于绘制和更新模拟的图形界面,而matplotlib用于绘制随时间变化的人群状态图表。
# 状态:
# S0表示易感者S
# S1表示感染者I
# S2表示治愈者R
# S3表示潜伏者E
# 规则:
# 1. 当S=S0时,为易感者,被感染率为p=k*(上下左右邻居的感染者)/4+l*(左上左下右上右下邻居的感染者)/4,概率c1变为潜伏者,概率1-c1变为感染者
# 2. 当S=S1时,为感染者,具有一定的感染能力,等待t_max时间,会自动变为S2治愈者,染病时间初始化为0
# 3. 当S=S2时,为治愈者,[具有一定的免疫能力,等待T_max时间,会自动变为S0易感者,免疫时间初始化为0],改为永久免疫
# 4. 当S=S3时,为潜伏者,等待t1_max时间(潜伏时间),会自动变为S1感染者,潜伏时间初始化为0,
from pylab import *
import random
import numpy as np
import pygame
import sys
import matplotlib.pyplot as plt
# 初始化相关数据
k=0.85 #上下左右概率
l=0.55 #其它概率
c1=0.4 #c1概率变为潜伏者
t1_max=15 #潜伏时间
t_max=50 #治愈时间
T_max=75 #免疫时间
# p = np.array([0.6, 0.4])
# probability = np.random.choice([True, False],
# p=p.ravel()) # p(感染or潜伏)=(self.s1_0*k+self.s1_1*l) p(易感)=1-(self.s1_0*k+self.s1_1*l)
def probablity_fun():
np.random.seed(0)
# p = np.array([(self.s1_0*k+self.s1_1*l),1-(self.s1_0*k+self.s1_1*l)])
p = np.array([0.6, 0.4])
probability = np.random.choice([True, False],
p=p.ravel()) # p(感染or潜伏)=(self.s1_0*k+self.s1_1*l) p(易感)=1-(self.s1_0*k+self.s1_1*l)
return probability
RED = (255, 0, 0)
GREY = (127, 127, 127)
Green = (0, 255, 0)
BLACK = (0, 0, 0)
"""细胞类,单个细胞"""
class Cell:
# 初始化
stage = 0
def __init__(self, ix, iy, stage):
self.ix = ix
self.iy = iy
self.stage = stage #状态,初始化默认为0,易感者
# self.neighbour_count = 0 #周围细胞的数量
self.s1_0 = 0 #上下左右为感染者的数量
self.s1_1 = 0 #左上左下右上右下感染者的数量
self.T_ = 0 #免疫时间
self.t_ = 0 #患病时间
self.t1_ = 0 #潜伏时间
# 计算周围有多少个感染者
def calc_neighbour_count(self):
count_0 = 0
count_1 = 0
pre_x = self.ix - 1 if self.ix > 0 else 0
for i in range(pre_x, self.ix+1+1):
pre_y = self.iy - 1 if self.iy > 0 else 0
for j in range(pre_y, self.iy+1+1):
if i == self.ix and j == self.iy: # 判断是否为自身
continue
if self.invalidate(i, j): # 判断是否越界
continue
if CellGrid.cells[i][j].stage == 1 or CellGrid.cells[i][j] == 3 : #此时这个邻居是感染者
#如果是在上下左右
if (i==self.ix and j==self.iy-1) or \
(i==self.ix and j==self.iy+1) or \
(i==self.ix-1 and j==self.iy) or \
(i==self.ix+1 and j==self.iy):
count_0+=1
else:
count_1+=1
# print(count_0)
self.s1_0 = count_0
# if self.s1_1!=0:
# print(count_1,count_0,self.ix,self.iy)
self.s1_1 = count_1
# 判断是否越界
def invalidate(self, x, y):
if x >= CellGrid.cx or y >= CellGrid.cy:
return True
if x < 0 or y < 0:
return True
return False
# 定义规则
def next_iter(self):
# 规则1,易感者
if self.stage==0:
probability=random.random()#生成0到1的随机数
s1_01 = self.s1_0 * k + self.s1_1 * l
if (s1_01>probability) and (s1_01!=0):
p1 = random.random()
if p1>c1:
self.stage=1
else:
self.stage=3
else:
self.stage = 0
# 规则2,感染者
elif self.stage == 1:
if self.t_ >= t_max:
self.stage = 2
else:
self.t_ = self.t_ + 1
# 规则3,治愈者(永久免疫规则)
elif self.stage == 2:
if self.T_ >= T_max:
self.stage = 0
else:
self.T_ = self.T_ + 1
# 规则4,潜伏者
elif self.stage == 3:
if self.t1_ >= t1_max:
self.stage = 1 # 转变为感染者
else:
self.t1_ += 1
"""细胞网格类,处在一个长cx,宽cy的网格中"""
class CellGrid:
cells = []
cx = 0
cy = 0
# 初始化
def __init__(self, cx, cy):
CellGrid.cx = cx
CellGrid.cy = cy
for i in range(cx):
cell_list = []
for j in range(cy):
cell = Cell(i, j, 0) #首先默认为全是易感者
if (i == cx/2 and j ==cy/2) or (i==cx/2+1 and j==cy/2) or (i==cx/2+1 and j==cy/2+1):#看26行就可以了
cell_list.append(Cell(i,j,1))
else:
cell_list.append(cell)
CellGrid.cells.append(cell_list)
def next_iter(self):
for cell_list in CellGrid.cells:
for item in cell_list:
item.next_iter()
def calc_neighbour_count(self):
for cell_list in CellGrid.cells:
for item in cell_list:
item.calc_neighbour_count()
def num_of_nonstage(self):
# global count0_,count1_,count2_
count0 = 0
count1 = 0
count2 = 0
count3 = 0
for i in range(self.cx):
for j in range(self.cy):
# 计算全部的方格数
cell = self.cells[i][j].stage
if cell == 0:
count0 += 1
elif cell == 1:
count1 += 1
elif cell == 2:
count2 += 1
elif cell == 3:
count3 += 1
return count0, count1, count2, count3
'''界面类'''
class Game:
screen = None
count0 = 0
count1 = 9
count2 = 0
count3 = 0
def __init__(self, width, height, cx, cy):#屏幕宽高,细胞生活区域空间大小
self.width = width
self.height = height
self.cx_rate = int(width / cx)
self.cy_rate = int(height / cy)
self.screen = pygame.display.set_mode([width, height])#
self.cells = CellGrid(cx, cy)
def show_life(self):
for cell_list in self.cells.cells:
for item in cell_list:
x = item.ix
y = item.iy
if item.stage == 0:
pygame.draw.rect(self.screen, GREY,
[x * self.cx_rate, y * self.cy_rate, self.cx_rate, self.cy_rate])
elif item.stage == 2:
pygame.draw.rect(self.screen, Green,
[x * self.cx_rate, y * self.cy_rate, self.cx_rate, self.cy_rate])
elif item.stage == 1:
pygame.draw.rect(self.screen, RED,
[x * self.cx_rate, y * self.cy_rate, self.cx_rate, self.cy_rate])
elif item.stage == 3:
pygame.draw.rect(self.screen, BLACK,
[x * self.cx_rate, y * self.cy_rate, self.cx_rate, self.cy_rate])
# def count_num(self):
# self.count0, self.count1, self.count2,self.count3 = self.cells.num_of_nonstage()
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
if __name__ == '__main__':
count0_ = []
count1_ = []
count2_ = []
count3_ = []
pygame.init()
pygame.display.set_caption("传染病模型")
game = Game(800, 800, 200, 200)
clock = pygame.time.Clock()
k1 = 0
while True:
k1 += 1
print(k1)
# game.screen.fill(GREY)#底部全置灰
clock.tick(100) # 每秒循环10次
for event in pygame.event.get():
if event.type == pygame.QUIT:
sys.exit()
game.cells.calc_neighbour_count()
count0, count1, count2,count3 = game.cells.num_of_nonstage()
# count0,count1,count2 = game.count_num()
count0_.append(count0)
count1_.append(count1)
count2_.append(count2)
count3_.append(count3)
if count2 > 200*190: # 退出条件
break
plt.plot(count0_, color='y', label='易感者')
plt.plot(count3_, color='b', label='潜伏者')
plt.plot(count1_, color='r', label='感染者')
plt.plot(count2_, color='g', label='治愈者')
# plt.ylim([0,80000])
plt.legend()
plt.xlabel('时间单位')
plt.ylabel('人数单位')
plt.pause(0.1)#0.1秒停一次
plt.clf()#清除
# plt.close()#退出
game.show_life()
pygame.display.flip()
game.cells.next_iter()
plt.show() #显示

右侧图是随着时间推移的人群状态变化曲线图,横轴表示时间,纵轴表示人数。不同颜色的曲线代表不同状态的人群数量:黄色曲线代表易感者(S0),蓝色曲线代表潜伏者(S3),红色曲线代表感染者(S1),绿色曲线代表治愈者(S2)。从曲线图可以看出,随着时间的推移,感染者人数先增加后减少,治愈者人数逐渐增加,潜伏者人数有一个短暂的峰值,而易感者人数则持续减少。这反映了疾病传播和人群免疫状态的动态变化。
2.7 数值计算方法与微分方程求解
在使用Python求微分方程的数值解或函数极值时,你可能会发现其与MATLAB在使用上有所不同。但你有没有想过,Python是如何求出这些数值解的呢?这背后涉及到的算法,通常会在工程数学和数值分析课程中学到。为了帮助大家更好地理解这些计算的基本原理,我们特别增加了一节内容,介绍一些基础的数值计算方法。如果你感兴趣,甚至可以尝试自己编写一个求解器。
2.7.1 Python通过什么求数值解
在Python中,数值计算方法主要依赖于一些专门的库,如NumPy、SciPy和SymPy等。这些库提供了丰富的数学函数和算法,用于处理线性代数、微积分、优化问题等。例如,SciPy中的scipy.optimize模块可以用于求解函数的极值,scipy.integrate模块可以用于数值积分,而scipy.linalg模块则提供了线性代数的相关功能。通过这些工具,我们可以在Python中有效地进行数值计算和求解微分方程。
数值计算方法是一种求解数学问题的近似方法,它在计算机上被广泛应用于各种数学问题的求解。无论是在科学研究还是工程技术中,计算方法都扮演着重要的角色。随着计算机技术的快速发展,计算方法已经成为理工科学生的一门必修课程。计算方法主要研究微积分、线性代数和常微分方程中的数学问题,内容涵盖插值和拟合、数值微分和积分、线性方程组的求解、矩阵特征值和特征向量的计算,以及常微分方程的数值解等。
在Python中,类似MATLAB中的fsolve和odeint这样的函数,正是依赖于这些数值计算方法来工作的。下面,我们将介绍几种经典的数值计算方法。
2.7.2 梯度下降法
梯度下降法是解决优化问题的一种普遍手段,尤其在机器学习和深度学习领域中。其核心思路是:从一个初始位置开始,沿着目标函数梯度的相反方向(即最速下降方向)逐步更新位置,直至达到最小值点。在Python中,我们通常利用NumPy等工具包来计算梯度,并按照梯度下降的更新规则调整变量值。
其基本原理简洁明了,即从一个初始点出发,计算当前点的梯度,并依照以下迭代规则进行更新:
$$ x{t+1} \leftarrow x{t} - \alpha \cdot \text{grad}(f). \tag{2.7.1}
$$ 当前后两次迭代的函数值之差满足一个很小的阈值(误差的容许范围)时我们认为迭代基本成功。或者从另一个角度,由于极值点的偏导数为$0$,那么当梯度的模接近$0$时,也可认为找到了极小值点。不过,个人建议使用函数值差异作为更准确的判断标准。
注意:事实上,在机器学习的实际应用中,由于数据量庞大,梯度下降通常有三种变体:随机梯度下降、批量梯度下降和小批量梯度下降。此外,还可以引入动量等技术来优化梯度下降过程。这些内容将在后续章节详细介绍。
以函数的极值为例,我们利用梯度下降函数去进行求解:
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-6,4,100)
y=x**2+2*x+5
可以编写如下的梯度下降函数。
#将迭代的点描绘出来更直观形象
x_iter=1#设置x的初始值
yita=0.06#步长
count=0#记录迭代次数
while True:
count+=1
y_last=x_iter**2+2*x_iter+5
x_iter=x_iter-yita*(2*x_iter+2)
y_next=x_iter**2+2*x_iter+5
plt.scatter(x_iter,y_last)
if abs(y_next-y_last)<1e-100:
break
print('最小值点x=',x_iter,'最小值y',y_next,'迭代次数n=',count)
x=np.linspace(-4,6,100)
y=x**2+2*x+5
plt.plot(x,y,'--')
plt.show()
最终解得:
最小值点x= -0.9999999616185459 最小值y 4.000000000000002 迭代次数n= 139
已经非常接近精确解$-1$,虽然有一定误差但很小,结果也确实满足了我们预先设置的要求。图像如下:
2.7.3 Newton法
Newton法,也称为切线法,是一种寻找函数零点的有效方法。其思路是从一个初始估计值开始,不断迭代更新,直到找到零点或达到预定精度。在求解函数极值问题时, Newton法通过寻找函数导数的零点来实现。它的原理如图3.16所示:

import numpy as np
def f(x):
y=x**3-x-1#求根方程的表达式
return y
def g(x):
y=3*x**2-1#求根方程的导函数
return y
def main():
x_0=1.5 #取初值
e=10**(-9) #误差要求
L=0 #初始化迭代次数
while L<100: #采用残差来判断
x1=x_0-f(x_0)/g(x_0) #迭代公式,x(n+1)=x(n)-f(x(n))/f'(x(n))
x_0=x1
L=L+1 #统计迭代次数
if abs(f(x_0)-0)<e:
break
print(f"x1={x1}") #输出数值解
print(f(x_0)-0) # 验证解的正确性
print(f"L={L}") #输出迭代次数
if __name__ == '__main__':
main()
注意:Python中不需要像MATLAB那样使用特殊函数来控制结果的精度,因为Python的浮点数运算本身就具有较高的精度。
最终解得:
x1=1.3247179572447898 1.865174681370263e-13 L=4
程序能够利用 Newton法搜索到起始点最近的一个零点。
2.7.4 Euler 法与 Runge-Kutta 法
在数值计算微分方程的过程中,一个核心的概念是用差分方法来近似微分。Euler 法和Runge-Kutta 法都是基于这一思想发展而来的。图2.7.3给出了 Runge-Kutta 法的示意图:
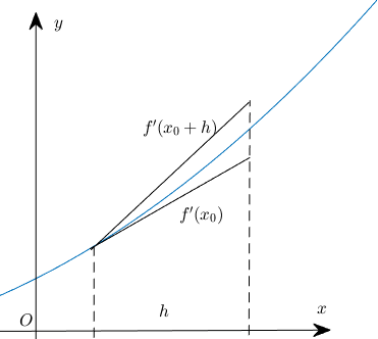
- 第一种思路是取$x_0$点和$(x_0+h)$点处斜率的平均值作为差分增量的斜率。这样,我们得到的差分增量就会更接近微分增量,这是改进 Euler 法的基本思想。
注意:使用当前点和下一点的导数值进行迭代的方法称为前向 Euler 法和后向 Euler 法。
- 另一种思路是在x_0和(x_0+h)之间取不同点的斜率进行平均,然后进行迭代。这是 Runge-Kutta 法的基本思想
典型的四阶 Runge-Kutta 法会使用四个不同点处的斜率进行迭代计算。经典四阶Runge-Kutta 法的迭代斜率如下:
$$ \begin{align} K{1} &\leftarrow f(x{i}, y{i}), \[0.5em] K{2} &\leftarrow f\left( x{i} + \frac{h}{2}, y{i} + \frac{K{1}}{2}\cdot h\right), \[0.5em] K{4} &\leftarrow f\left( x{i} + \frac{h}{2}, y{i} + \frac{K{2}}{2}\cdot h\right), \[0.5em] K{4} &\leftarrow f(x{i} + h, y{i} + K{3}h), \[0.5em] y{i+1} &\leftarrow y{i} + \frac{h}{6}(K{1} + 2K{2} + 2K{3} + K_{4}). \end{align} \tag{2.7.2}
$$ 我们可以编写一个程序自己实现 Runge-Kutta 法:
import math
import numpy as np
import matplotlib.pyplot as plt
def runge_kutta(y, x, dx, f):
""" y is the initial value for y
x is the initial value for x
dx is the time step in x
f is derivative of function y(t)
"""
k1 = dx * f(y, x)
k2 = dx * f(y + 0.5 * k1, x + 0.5 * dx)
k3 = dx * f(y + 0.5 * k2, x + 0.5 * dx)
k4 = dx * f(y + k3, x + dx)
return y + (k1 + 2 * k2 + 2 * k3 + k4) / 6.
t = 0.
y = 0.
dt = .1
ys, ts = [0], [0]
def func(y, t):
return 1/(1+t**2)-2*y**2
while t <= 10:
y = runge_kutta(y, t, dt, func)
t += dt
ys.append(y)
ts.append(t)
YS=odeint(func,y0=0, t=np.arange(0,10.2,0.1))
plt.plot(ts, ys, label='runge_kutta')
plt.plot(ts, YS, label='odeint')
plt.legend()
plt.show()
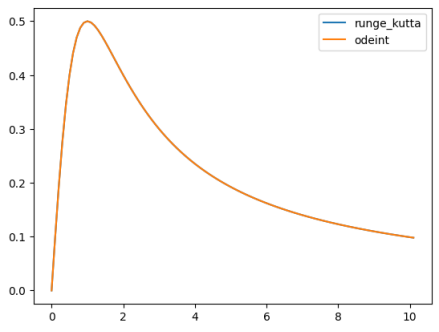
odeint函数的对比runge_kutta)和 Python 的odeint函数。水平轴代表时间变量t,范围从0到10,垂直轴代表函数y(t)的值。
图中,我们可以看到两条曲线:一条代表 Runge-Kutta 法,另一条代表odeint函数。两条曲线从t = 0时的同一个初始y值开始,随着时间的推移而分开。Runge-Kutta 方法的曲线呈现出开始时的急剧上升,达到顶点后逐渐下降,并在t接近10时趋近于零。odeint函数的曲线紧跟 Runge-Kutta 方法的曲线,表明两种方法提供了相似的微分方程解,虽然存在轻微的变化。
我们可以用自己写的龙格库塔测试洛伦兹系统的结果:
import numpy as np
def move(P, steps, sets):
x, y, z = P
sgima, rho, beta = sets
# 各方向的速度近似
dx = sgima * (y - x)
dy = x * (rho - z)
dz = x * y - beta * z
return [x + dx * steps, y + dy * steps, z + dz * steps]
# 设置sets参数
sets = [10., 28., 3.]
t = np.arange(0, 30, 0.01)
# 位置1:
P0 = [0., 1., 0.]
P = P0
d = []
for v in t:
P = move(P, 0.01, sets)
d.append(P)
dnp = np.array(d)
# 位置2:
P02 = [0., 1.01, 0.]
P = P02
d = []
for v in t:
P = move(P, 0.01, sets)
d.append(P)
dnp2 = np.array(d)
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(dnp[:, 0], dnp[:, 1], dnp[:, 2])
ax.plot(dnp2[:, 0], dnp2[:, 1], dnp2[:, 2])
plt.show()
在洛伦兹方程上测试得到结果如图2.7.5所示。洛伦兹方程实际上就是“蝴蝶效应”的数学原理,它的曲线非常像一只蝴蝶。这是在混沌系统研究中得到的结论,当给这个系统一个微小的扰动就会引起极大的变化。也证明这一系统是不稳定的。
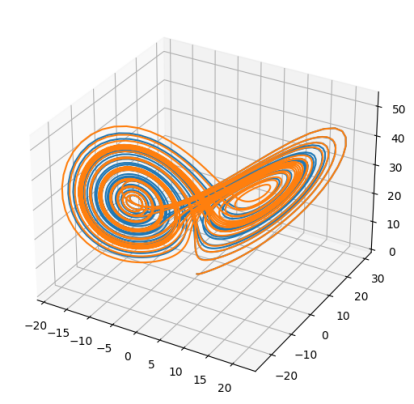
2.7.5 Crank-Nilkson 法在热传导问题中的应用
本节参考自 【数学建模之Python】13.手撕抛物型方程的差分解法(如一维热传导方程)_crank-nicolson差分格式-CSDN博客 ,特别鸣谢!
Crank-Nicolson 法是数值分析中一种用于求解热传导方程和类似偏微分方程的时间推进技术。与纯显式或隐式方法相比,它通过时间中心差分的方式,既稳定又准确。在本节中,我们将探讨如何使用Crank-Nicolson 法求解一维热传导问题,并将其与传统的显式和隐式方法进行比较。
首先,我们需要设定一些初始参数,包括热传导系数、空间和时间的最大范围、步长,以及相关的网格比。在给定这些参数后,我们用Python创建一个矩阵来初始化温度分布,并设定边界条件。在边界处,温度随时间的变化采用指数函数来模拟。本文所示的代码包含几个不同的数值方法:
- 古典显式方法:一种简单但当时间步长较大时可能不稳定的方法;
- 古典隐式方法:利用逆矩阵求解,计算上更稳定,适用于更大的时间步长;
- 古典隐式方法(追赶法):一个更高效的算法,避免了直接计算矩阵的逆;
- Crank-Nicolson 法(逆矩阵):结合显式和隐式方法的优点,提高了稳定性和精确度;
- Crank-Nicolson 法(追赶法):同样结合了显式和隐式的优点,但使用追赶法提高计算效率;
除此之外,我们还提供了一个精确解函数,用于验证数值解的准确性。所有的数值方法均以Python函数的形式实现,并在结束时将结果输出到Excel文件中,便于分析和对比。
import numpy as np
import pandas as pd
import datetime
start_time = datetime.datetime.now()
np.set_printoptions(suppress=True)
def left_boundary(t): # 左边值
return np.exp(t)
def right_boundary(t): # 右边值
return np.exp(t + 1)
def initial_T(x_max, t_max, delta_x, delta_t, m, n): # 给温度T初始化
T = np.zeros((n + 1, m + 1))
for i in range(m + 1): # 初值
T[0, i] = np.exp(i * delta_x)
for i in range(1, n + 1): # 注意不包括T[0,0]与T[0,-1]
T[i, 0] = left_boundary(i * delta_t) # 左边值
T[i, -1] = right_boundary(i * delta_t) # 右边值
return T
# 一、古典显格式
def one_dimensional_heat_conduction1(T, m, n, r):
# 可以发现当r>=0.5时就发散了
for k in range(1, n + 1): # 时间层
for i in range(1, m): # 空间层
T[k, i] = (1 - 2 * r) * T[k - 1, i] + r * (T[k - 1, i - 1] + T[k - 1, i + 1])
return T.round(6)
# 二、古典隐格式(乘逆矩阵法)
def one_dimensional_heat_conduction2(T, m, n, r):
A = np.eye(m - 1, k=0) * (1 + 2 * r) + np.eye(m - 1, k=1) * (-r) + np.eye(m - 1, k=-1) * (-r)
a = np.ones(m - 1) * (-r)
a[0] = 0
b = np.ones(m - 1) * (1 + 2 * r)
c = np.ones(m - 1) * (-r)
c[-1] = 0
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
for k in range(1, n + 1): # 时间层range(1, n + 1)
F[0] = T[k - 1, 1] + r * T[k, 0]
F[-1] = T[k - 1, m - 1] + r * T[k, m]
for i in range(1, m - 2): # 空间层
F[i] = T[k - 1, i + 1] # 给F赋值
for i in range(1, m - 1):
T[k, 1:-1] = np.linalg.inv(A) @ F # 左乘A逆
return T.round(6)
# 三、古典隐格式(追赶法)
def one_dimensional_heat_conduction3(T, m, n, r):
a = np.ones(m - 1) * (-r)
a[0] = 0
b = np.ones(m - 1) * (1 + 2 * r)
c = np.ones(m - 1) * (-r)
c[-1] = 0
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
for k in range(1, n + 1): # 时间层range(1, n + 1)
F[0] = T[k - 1, 1] + r * T[k, 0]
F[-1] = T[k - 1, m - 1] + r * T[k, m]
y = np.zeros(m - 1)
beta = np.zeros(m - 1)
x = np.zeros(m - 1)
y[0] = F[0] / b[0]
d = b[0]
for i in range(1, m - 2): # 空间层
F[i] = T[k - 1, i + 1] # 给F赋值
for i in range(1, m - 1):
beta[i - 1] = c[i - 1] / d
d = b[i] - a[i] * beta[i - 1]
y[i] = (F[i] - a[i] * y[i - 1]) / d
x[-1] = y[-1]
for i in range(m - 3, -1, -1):
x[i] = y[i] - beta[i] * x[i + 1]
T[k, 1:-1] = x
return T.round(6)
# 四、Crank-Nicolson(乘逆矩阵法)
def one_dimensional_heat_conduction4(T, m, n, r):
A = np.eye(m - 1, k=0) * (1 + r) + np.eye(m - 1, k=1) * (-r * 0.5) + np.eye(m - 1, k=-1) * (-r * 0.5)
C = np.eye(m - 1, k=0) * (1 - r) + np.eye(m - 1, k=1) * (0.5 * r) + np.eye(m - 1, k=-1) * (0.5 * r)
for k in range(0, n): # 时间层
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
F[0] = r / 2 * (T[k, 0] + T[k + 1, 0])
F[-1] = r / 2 * (T[k, m] + T[k + 1, m])
F = C @ T[k, 1:m] + F
T[k + 1, 1:-1] = np.linalg.inv(A) @ F
return T.round(6)
# 五、Crank-Nicolson(追赶法)
def one_dimensional_heat_conduction5(T, m, n, r):
C = np.eye(m - 1, k=0) * (1 - r) + np.eye(m - 1, k=1) * (0.5 * r) + np.eye(m - 1, k=-1) * (0.5 * r)
a = np.ones(m - 1) * (-0.5 * r)
a[0] = 0
b = np.ones(m - 1) * (1 + r)
c = np.ones(m - 1) * (-0.5 * r)
c[-1] = 0
for k in range(0, n): # 时间层
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
F[0] = r * 0.5 * (T[k, 0] + T[k + 1, 0])
F[-1] = r * 0.5 * (T[k, m] + T[k + 1, m])
F = C @ T[k, 1:m] + F
y = np.zeros(m - 1)
beta = np.zeros(m - 1)
x = np.zeros(m - 1)
y[0] = F[0] / b[0]
d = b[0]
for i in range(1, m - 1):
beta[i - 1] = c[i - 1] / d
d = b[i] - a[i] * beta[i - 1]
y[i] = (F[i] - a[i] * y[i - 1]) / d
x[-1] = y[-1]
for i in range(m - 3, -1, -1):
x[i] = y[i] - beta[i] * x[i + 1]
T[k + 1, 1:-1] = x
return T.round(6)
def exact_solution(T, m, n, r, delta_x, delta_t): # 偏微分方程精确解
for i in range(n + 1):
for j in range(m + 1):
T[i, j] = np.exp(i * delta_t + j * delta_x)
return T.round(6)
a = 1 # 热传导系数
x_max = 1
t_max = 1
delta_x = 0.1 # 空间步长
delta_t = 0.1 # 时间步长
m = int((x_max / delta_x).__round__(4)) # 长度等分成m份
n = int((t_max / delta_t).__round__(4)) # 时间等分成n份
t_grid = np.arange(0, t_max + delta_t, delta_t) # 时间网格
x_grid = np.arange(0, x_max + delta_x, delta_x) # 位置网格
r = (a * delta_t / (delta_x ** 2)).__round__(6) # 网格比
T = initial_T(x_max, t_max, delta_x, delta_t, m, n)
print('长度等分成{}份'.format(m))
print('时间等分成{}份'.format(n))
print('网格比=', r)
p = pd.ExcelWriter('有限差分法-一维热传导-题目1.xlsx')
T1 = one_dimensional_heat_conduction1(T, m, n, r)
T1 = pd.DataFrame(T1, columns=x_grid, index=t_grid) # colums是列号,index是行号
T1.to_excel(p, '古典显格式')
T2 = one_dimensional_heat_conduction2(T, m, n, r)
T2 = pd.DataFrame(T2, columns=x_grid, index=t_grid) # colums是列号,index是行号
T2.to_excel(p, '古典隐格式(乘逆矩阵法)')
T3 = one_dimensional_heat_conduction3(T, m, n, r)
T3 = pd.DataFrame(T3, columns=x_grid, index=t_grid) # colums是列号,index是行号
T3.to_excel(p, '古典隐格式(追赶法)')
T4 = one_dimensional_heat_conduction4(T, m, n, r)
T4 = pd.DataFrame(T4, columns=x_grid, index=t_grid) # colums是列号,index是行号
T4.to_excel(p, 'Crank-Nicolson格式(乘逆矩阵法)')
T5 = one_dimensional_heat_conduction5(T, m, n, r)
T5 = pd.DataFrame(T5, columns=x_grid, index=t_grid) # colums是列号,index是行号
T5.to_excel(p, 'Crank-Nicolson格式(追赶法)')
T6 = exact_solution(T, m, n, r, delta_x, delta_t)
T6 = pd.DataFrame(T6, columns=x_grid, index=t_grid) # colums是列号,index是行号
T6.to_excel(p, '偏微分方程精确解')
p.save()
end_time = datetime.datetime.now()
print('运行时间为', (end_time - start_time))
通过比较这些方法,我们可以更好地了解不同算法在求解偏微分方程时的性能和适用场景。Crank-Nicolson方法的引入提供了一个稳定且准确的解决方案,特别适合于那些对时间步长有限制的问题。 我们的程序记录了计算过程的开始和结束时间,这样可以衡量不同方法的运算效率。这个案例不仅展示了如何在Python中实现复杂的数值算法,而且还揭示了数值解法在工程和科学研究中的重要性,特别是在解决现实世界问题时。