第3章 函数极值与规划模型
内容:@若冰(马世拓)
审稿:@刘旭
排版&校对:@何瑞杰
在这一章中我们将介绍函数极值与规划模型。约束条件下的极值求解是优化问题和运筹学研究的重点,也是各大数学建模竞赛中考察的重难点。它主要针对的就是及目标函数在约束条件下的极值,以及多种方案中的最优方案。本章主要涉及到的知识点有:
- 线性规划的基本模型与求解
- 非线性规划的基本模型与求解
- 整数规划的基本模型与求解
- 动态规划的基本模型与求解
- 多目标规划的一般策略
注意:本章内容也可以在凸优化理论相关资料中学习到,是比较难的一章。除了Matlab、Python以外有很多优化求解软件例如Lingo、gurobi等也适合做优化问题。
3.1 从线性代数到线性规划
我想各位在中学阶段其实已经是对线性规划有所了解了,不过如果有些学校没学的话也没关系。在这一节当中我们会回顾以前中学接触到的线性规划,补充一些线性代数的知识和Python解线性代数问题的指令,最后引出线性规划的基本形式。数学建模是一门应用数学课程,与基础数学不同,我这里不打算抢读者线性代数老师的饭碗太严重,但我们会尽可能多补充一些基础的常用的有关理论。
3.1.1 中学阶段线性规划的局限性
在高中阶段我们其实就学习过线性规划的知识,但是当时我们可能没有觉得它有多重要所以可能忘掉了。我们通过一个例子回忆一下:
例3.1 若$x$, $y$满足条件$\displaystyle \left{\begin{align} &x + y \geqslant 4\ &x - y \leqslant 2 \ &y \leqslant 3 \end{align}\right.$,则$z = 3x + y$ 的最小值为() A. 18 B. 10 C. 6 D. 4
我想这个问题大家不会感到陌生了。答案很简单,选择C。血脉觉醒的高中生们会将不等式组中的不等式两两配对成三个二元一次方程组求解,得到三个点,最后把三个点分别代入$z=3x+y$最后得到最小值。这是比较快的方法,在90%的情况下这种策略是很奏效的。而学霸们也会采取画图的策略,平移直线来求解。这个问题的可行域如图2.1所示:
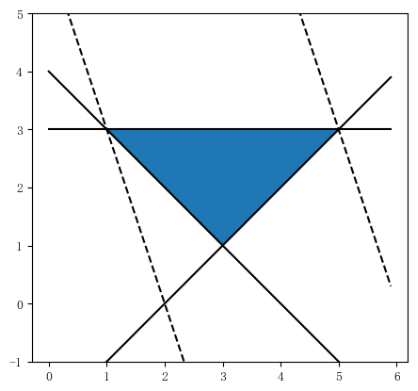
这个题目的解其实很明显,就是把不等式组里面每个不等式在平面直角坐标系中表示出来,然后根据不等号的方向确定可行域。将目标函数进行移项以后转化为$y=-3x+z$,通过平移直线的方式找到可行域内使目标函数截距最大的点,就是正确答案。大家回忆起来了吗?
注意:平移直线法是一种通用方法,解方程组得到的最优解很多情况下确实有效但不排除有些特殊情况下可行域是开放的,这个时候不一定存在最小值或最大值。
我为什么把线性规划作为第一个知识点呢?因为线性规划是真的非常重要也非常实用,也最贴近一个入门级小白认识数学建模所具备的数学基础。线性规划的实际应用有很多,比如说:我们可能见过这样一种问题,去运输一批货物的时候大车能运五箱,小车只能运三箱,但我们大车和小车数量都有限,怎么安排运输方案能够在车辆够用的情况下运费还能最小?如果我们把大车数量记为$x$,小车数量记为$y$,那么除了$x$和$y$的范围,$5x+3y$也有自己的一个范围,算上运费作为优化目标,这不就构成了一个线性规划吗?背景熟悉吧,甚至于有一种小学应用题的恐惧感。
再打个比方,生产原料问题,生产产品A、B需要原材料甲、乙、丙;生产一吨A需要多少多少甲、多少多少乙、多少多少丙,这样就有了对AB的三个原料约束。再来一个利润最大作为目标,这也是线性规划。我猜很多读者看到这些例子可能就会暗想:“这就是数学建模?我怎么感觉梦回小学应用题?难不成我被骗了?”,是的,数学建模其实没有那么恐怖,小时候我们做的是应用题,到大了我们只不过是需要用更多知识和编程方法解背景更产业化更学术化的应用题。因为这是一门应用数学学科。
我们大概可以总结出,中学的线性规划通常就两个变量$x$和$y$,约束条件三个不等式,最后一个线性的形如$z=ax+by$(这里$a$和$b$都是常数)的目标函数。这样的式子我们解方程可以解,画图也可以解,总能在两分钟之内算出正确结果。但在实际情况中,问题真的有这么容易吗?其实不然。同样是拿生产问题做文章,如果我们这里生产的原料不止甲乙丙三种呢(通常在有机化合物合成的时候原料可能有十几种甚至上百种),产出的产品也不止AB而是能够产出数十种化合物,还能简单地用高中的方法写吗?
所以我们说,中学的规划存在这样一些局限性:
- 决策变量(如果不好理解暂且称之为自变量吧)往往不止两三个;
- 当变量个数超过三个的时候还能在直角坐标系里面画图吗?不能了;
- 约束条件往往不止三个不等式,不等式可能比变量更多一些;
- 当变量较多的时候,还可能出现方程形式下的约束;
- 中学阶段我们只讨论了线性规划,但如果不等式或者目标函数非线性呢。
这么多情况不知读者朋友会不会被吓到。如果十几个甚至几十个不等式方程组成约束条件,那我草稿纸甚至不知道写不写的下,况且中学阶段没有接触过高维问题。于是,为了以更简单的形式描述更一般的线性规划,我们需要借助一样数学工具——线性代数。
有关于线性代数基本知识的回顾与编程实现,大家可以参考下一节中的内容。如果有学习过线性代数的读者,可以跳过3.2.1节。
3.1.2 线性规划的基本形式
前面我们已经看到,中学线性规划的局限性在于难以描述多约束、多变量,但无论是目标函数还是方程还是不等式,我们都可以看成是一个系数向量与变量向量在做乘法(例如,$2a+3b-c$实际上可以看成向量$[2,3,-1]$与向量$[a,b,c]$做内积)。多个约束无非就是把多个向量拼接在一块做成了一个矩阵而已。
我们把所有的方程约束中系数做成系数矩阵$A{\text{eq}}$,等号右边的常数作为列向量$b\text{eq}$;不等式约束中的系数矩阵$A$和不等号右边的常数$b$,为了方便起见通常将不等式统一为小于等于;变量$x$在向量$l_b$到$u_b$之间取值;目标函数的系数向量为$c$,那么线性规划的标准形式就如下所示:
$$ \begin{align} \text{minimize}~&f = c^{\top}x\[0.5em] \text{subject to}~& Ax \leqslant b\ & A{\text{eq}}\,x = b{\text{eq}}\ &l{b} \leqslant x \leqslant u{b} \end{align} \tag{3.1.1}
$$
这里的$\leqslant$是指两边向量的对应分量的小于等于关系,即对任意$i$满足$(Ax){i} \leqslant b{i}$。第二行的 subject to 也常简写为 s.t.
为了方便matlab编程,我们通常将问题统一为函数极小值问题,不等约束统一为小于等于。如果原问题是最大值或者有大于等于,那就乘$-1$进行取反即可。可能我说这么半天读者并不一定能理解,这里我举一个例子,在matlab中整理一个线性规划的标准形式:
例3.2 将该线性规划整理为标准形式并将各矩阵存储在matlab变量区中:
$$ \begin{align} \text{minimize}~&f = 3x{1} + 2x{2} - x{3}\[0.5em] \text{s.t.}~ & 3x{1} - x{2} + x{3} \leqslant 18\ & x{1} + 2x{2} \leqslant 16\ &x{1} + x{2} + x{3} \geqslant 2\ &x{1} + 2x{2} + 3x{3} = 15\ &x{1} - x{3} = 4\ & 0 \leqslant x_{i} \leqslant 16, ~i=1,2,3. \end{align} \tag{3.1.2}
$$ 我们注意到有一个不等式里面是大于等于,所以左右两边乘-1;一个不等式一个方程里面缺少了一项,这是因为缺少的那一项系数是$0$。把各个矩阵和向量存在matlab里面:
==这里缺了东西==
3.2 使用Numpy进行矩阵运算
3.2.1 线性代数基本知识回顾
线性代数是一门基础数学科目,基本上所有理工科学生大一的时候都得学线性代数。如果是数学系可能学的就是高等代数了。这门课主要是研究矩阵与向量的数学理论,也会探究线性方程组的解等相关问题。我并不是一个线代老师,这里也不打算抢线代老师的饭碗,这一小节我们仅仅引入线性代数中比较重要的一些定义和计算方法。
我相信大多数同学高中毕业是记得向量这个概念的,但中学阶段我们也仅仅是接触到了三维向量。事实上向量的维数可以是很多维,从代数的意义上你可以认为向量是一个集合,从几何的意义上你又可以认为向量是一个$n$维 Euclid 空间中的一个点:
$$ \boldsymbol{x} = [x{1}, x{2}, \dots, x_{n}]^{\top} \tag{3.2.1}
$$
注意:向量常用粗体($\boldsymbol{a}$)或带箭头标识的字母($\vec{a}$)表示。在本教程中统一用前者;在不引起歧义的情形下,不对向量和矩阵的符号加粗。
和二维、三维空间中的向量一样,高维空间中的向量同样可以进行加减运算、数量乘运算和数乘运算。但毕竟这是一门应用数学课程,我们不打算把太多精力放在任何一本线代课本里面都能找到的公式上,使用matlab举例子恐怕会更加直观。从程序设计的角度来看,如果读者接触过C语言应该会了解数组的概念,而在C++语言中STL里面已经包含了vector类型。
数通过集合形成了向量,那向量集合以后又会变成什么呢?如果向量只是沿着同一个方向进行拼接,那么得到的只不过是一个更长一些的向量。但如果是在纵向上做拼接,那么我们或许可以把一个向量排成表格:
$$ A = \left[ \begin{matrix} a{1,1} & \cdots & a{1,n}\ \vdots & \ddots & \vdots\ a{m,1} & \cdots & a{m,n} \end{matrix} \right]_{m \times n} \tag{3.2.2}
$$
注意:
- 本教程中的矩阵统一使用方括号;
- 右下角的 $m \times n$ 表示矩阵的形状,在上文的例子中,若所有分量均为实数,则 $A \in \mathbb{R}^{m \times n}$;
- 矩阵下标常用 $a{ij}$ 表示。为避免歧义,本教程统一记为 $a{i,j}$。
这个数表要求每个矩阵的维度相同,排成的这个表格就可以称作一个矩阵。那么矩阵作为向量的集合,自然也保留了向量的一些特性,包括行列相同的矩阵的加减法、数量乘。比较有趣的是矩阵的乘法,它把两个矩阵分别按行、列规约:
$$ A{m \times n} B{n \times k} = \left[ \begin{matrix} \boldsymbol a{1}^{\top}\ \boldsymbol a{2}^{\top}\ \vdots\ \boldsymbol{a}{m}^{\top} \end{matrix} \right] [\boldsymbol{b}{1}, \dots, \boldsymbol{b}{k}] = \left[ \begin{matrix} \boldsymbol{a}{1}^{\top}\boldsymbol{b}{1} & \cdots & \boldsymbol{a}{1}^{\top}\boldsymbol{b}{k}\ \vdots & \ddots & \vdots \ \boldsymbol{a}{m}^{\top}\boldsymbol{b}{1} & \cdots & \boldsymbol{a}{m}^{\top}\boldsymbol{b}{k} \end{matrix} \right]{m \times k},\tag{3.2.3}
$$ 其中对所有的$i$和$j$,都有$\boldsymbol a{i}, \boldsymbol{b}{j} \in \mathbb{R}_{n}$。矩阵排列好以后除了按行可以规约为一群向量的纵向分布,也可以按列规约成一群向量的横向分布。于是才有了(2.10)中矩阵乘法的这个计算方法。每一项都是两个同为$n$维的向量数乘。
注意:矩阵乘法的维度要求第一个矩阵的列数和第二个矩阵的行数相等,因此要注意维度问题。另外矩阵的乘法没有交换律,在$AB$和$BA$都存在时,一般有$\color{red} AB \ne BA$ 。
==需要修改,改成“平行多面体的体积”== 那我们能否类比向量的模,提出“矩阵的模”这样一个概念呢?在线性代数中确实存在这样一个类似的概念,这个概念叫行列式:
行列式虽然同样是排成了一个表,但注意,矩阵是一个表格,行列式是一个数,它的值是可以算出来的!有关行列式的计算方法有很多,但最经典最通用的方法是代数余子式展开法。代数余子式的本质就是递归式求解,将行列式A中下标为(i,j)的元素所在行和所在列全部去除以后求新的行列式,再乘上对应的符号。而对于行列式A,计算定义为:
注意:行列式除了按某一行展开也可以按某一列展开,这一展开行或展开列的选取是任意的,方便计算即可。另外,矩阵可以不要求行列数相等但行列式必须行列数相等!
而递归到最后,我们逃不开最低的二阶行列式求解。二阶行列式的定义为:
将$n$阶行列式降低到$n-1$阶,$n-1$阶再降低为n-2阶,逐层展开到最后二阶,整个行列式求解就可以完成了。不过高阶行列式如果不是特殊行列式计算会有些复杂,我们可以将这个过程交给计算机程序来完成。
这样我们就可以在命令行输出矩阵A对应的行列式的值。有了行列式的概念,我们可以用它定义矩阵的逆矩阵计算方法。一个行列数均为n的矩阵的逆矩阵满足这样的定义:
定义2.1.2 方阵$A$的逆$A^{-1}$若存在,则满足下面的等式:
$$ A^{-1}A = AA^{-1} = I = \left[ \begin{matrix} 1 \ &1\ &&\ddots&\ &&&1 \end{matrix} \right] = \text{diag}(1, \dots, 1).\tag{3.2.4}
$$
3.2.2 numpy基本使用
使用numpy之前首先需要导入模块:
import numpy as np
接下来我们需要了解一下numpy的几种属性:
ndim:维度shape:行数和列数size:元素个数
print('number of dim:',array.ndim) # 维度
# number of dim: 2
print('shape :',array.shape) # 行数和列数
# shape : (2, 3)
print('size:',array.size) # 元素个数
# size: 6
1 Numpy 的创建array
array:创建数组dtype:指定数据类型zeros:创建数据全为0ones:创建数据全为1empty:创建数据接近0arrange:按指定范围创建数据linspace:创建线段
创建数组
a = np.array([2,23,4]) # list 1d
print(a)
# [2 23 4]
指定数据类型
a = np.array([2,23,4],dtype=np.int64)
print(a.dtype)
# int 64
创建特定数据
a = np.array([[2,23,4],[2,32,4]]) # 2d 矩阵 2行3列
print(a)
"""
[[ 2 23 4]
[ 2 32 4]]
"""
2 numpy 的几种基本运算
import numpy as np
a=np.array([10,20,30,40]) # array([10, 20, 30, 40])
b=np.arange(4) # array([0, 1, 2, 3])c=a-b # array([10, 19, 28, 37])
c=a+b # array([10, 21, 32, 43])
c=a*b # array([ 0, 20, 60, 120])
c=b**2 # array([0, 1, 4, 9])
c=10*np.sin(a)
# array([-5.44021111, 9.12945251, -9.88031624, 7.4511316 ])
print(b<3)
# array([ True, True, True, False], dtype=bool)
a=np.array([[1,1],[0,1]])
b=np.arange(4).reshape((2,2))
print(a)
# array([[1, 1],
# [0, 1]])
print(b)
# array([[0, 1],
# [2, 3]])
c_dot = np.dot(a,b)
# array([[2, 4],
# [2, 3]])
c_dot_2 = a.dot(b)
# array([[2, 4],
# [2, 3]])
a=np.random.random((2,4))
print(a)
# array([[ 0.94692159, 0.20821798, 0.35339414, 0.2805278 ],
# [ 0.04836775, 0.04023552, 0.44091941, 0.21665268]])
np.sum(a) # 4.4043622002745959
np.min(a) # 0.23651223533671784
np.max(a) # 0.90438450240606416
print("a =",a)
# a = [[ 0.23651224 0.41900661 0.84869417 0.46456022]
# [ 0.60771087 0.9043845 0.36603285 0.55746074]]
print("sum =",np.sum(a,axis=1))
# sum = [ 1.96877324 2.43558896]
print("min =",np.min(a,axis=0))
# min = [ 0.23651224 0.41900661 0.36603285 0.46456022]
print("max =",np.max(a,axis=1))
# max = [ 0.84869417 0.9043845 ]
A = np.arange(2,14).reshape((3,4))
# array([[ 2, 3, 4, 5]
# [ 6, 7, 8, 9]
# [10,11,12,13]])
print(np.argmin(A)) # 0
print(np.argmax(A)) # 11
print(np.mean(A)) # 7.5
print(np.average(A)) # 7.5
print(np.cumsum(A))
# [2 5 9 14 20 27 35 44 54 65 77 90]
print(np.diff(A))
# [[1 1 1]
# [1 1 1]
# [1 1 1]]
A = np.arange(14,2, -1).reshape((3,4))
# array([[14, 13, 12, 11],
# [10, 9, 8, 7],
# [ 6, 5, 4, 3]])
print(np.sort(A))
# array([[11,12,13,14]
# [ 7, 8, 9,10]
# [ 3, 4, 5, 6]])
print(np.transpose(A))
print(A.T)
# array([[14,10, 6]
# [13, 9, 5]
# [12, 8, 4]
# [11, 7, 3]])
# array([[14,10, 6]
# [13, 9, 5]
# [12, 8, 4]
# [11, 7, 3]])
3 Numpy array 合并
import numpy as np
A = np.array([1,1,1])
B = np.array([2,2,2])
print(np.vstack((A,B))) # vertical stack
"""
[[1,1,1]
[2,2,2]]
"""
D = np.hstack((A,B)) # horizontal stack
print(D)
# [1,1,1,2,2,2]
C = np.concatenate((A,B,B,A),axis=0)
print(C)
"""
array([[1],
[1],
[1],
[2],
[2],
[2],
[2],
[2],
[2],
[1],
[1],
[1]])
"""
D = np.concatenate((A,B,B,A),axis=1)
print(D)
"""
array([[1, 2, 2, 1],
[1, 2, 2, 1],
[1, 2, 2, 1]])
"""
4 Numpy array的分割
import numpy as np
A = np.arange(12).reshape((3, 4))
print(A)
"""
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
"""
print(np.split(A, 2, axis=1))
"""
[array([[0, 1],
[4, 5],
[8, 9]]), array([[ 2, 3],
[ 6, 7],
[10, 11]])]
"""
print(np.split(A, 3, axis=0))
# [array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8, 9, 10, 11]])]
print(np.array_split(A, 3, axis=1)) #不等量分割
"""
[array([[0, 1],
[4, 5],
[8, 9]]), array([[ 2],
[ 6],
[10]]), array([[ 3],
[ 7],
[11]])]
3.3 线性规划的算法原理
前面我们简单的回顾了线性规划和线性代数的基本知识,接下来我们将具体的介绍线性规划的算法原理。
3.3.1 单纯形法
在2.1节的最后我们提出了线性规划的标准形式,但注意这种标准形式是针对程序设计工具而言的。如果读者有凸优化理论的背景可能会感到狐疑,说:为什么我看到的标准形式和你这里写的不太一样?是的,经典的凸优化教材会把模型写成另外一种形式:
$$ \begin{align} \text{maximize}~& f = c^{\top}X\[0.5em] \text{s.t.}~ &A^{}\tilde{X} = b^{}\ & X \geqslant 0. \end{align}\tag{3.3.1}
$$ 为了和2.1当中提出的标准形式区分,我们暂且把这种形式称作规范形式。规范形式求的是函数的极大值,并且把不等关系和等式关系统一为等式关系方便求解。读者朋友可能会有些疑惑,说:不等式怎么可以充当为方程呢?这就是一种数学思想。可能读者朋友可以理解方程是不等式的特例,但不一定理解不等式也可以视作方程的特例,我举个例子。比如对于不等式$2a+3b+c<10$,左边比右边小,但是小多少呢?我们把这个差额记作d,左边如果补上这个差额就可以写作$2a+3b+c+d=10$,这样就转化成了等式。这里的d被称为松弛变量。包括决策变量的上下界$l_b$和$u_b$也会被转化为不等关系引入松弛量。
在单纯形法中,我们解决问题通常从理论上都会把问题转换为规范形式来求解,对每一个不等式都引入一个松弛变量去增广我们的原问题。但这些松弛变量不会出现在目标函数当中。
注意:在程序设计中我们输入的是它的标准形式,而在matlab底层以规范形式进行运算,只是从标准形式到规范形式这个操作我们看不见。不等式条件中增广了n个松弛变量的同时等式条件也会增广,只不过在增广后的等式条件中松弛变量的系数都是0。
单纯形法的步骤包括如下几个步骤:
- 确定初始可行基和初始基可行解,并建立初始单纯形表。
- 在当前表的目标函数对应的行中,若所有非基变量的系数非正,则得到最优解,算法终止;否则进入下一步。
- 若单纯形表中$1 \cdots m$列构成单位矩阵,在$j=m+1\cdots n$列中,若有某个对应$x_k$的系数列向量$P_k \leqslant 0$,则停止计算。否则,转入下一步。
- 挑选目标函数对应行中系数最大的非基变量作为进基变量。假设$x{k}$为进基变量,按如下规则计算,可确定$x{u}$为出基变量,转下一步:$$\theta = \min \left.\left{ \frac{b{i}}{a{i,k}} \right| a{i,k} > 0 \right} = \frac{b{u}}{a{u,k}}, \tag{3.3.2}$$ 其中$b{i}$是规范型规划的常数项,$a_{i,k}$即为在第$i$个约束中变量$k$的系数。
- 以$a{u,k}$为主元素进行迭代,对$x_k$所对应的列向量进行如下变换:$$P{k} = [a{1,k}, a{2,k}, \dots, a{u,k}, \dots, a{m,k}]^{\top} = [0, 0, \dots, 1, \dots, 0]^{\top}\tag{3.3.3}$$ 也即令向量$P_{k}$除了第$u$个元素为$1$外其他元素都为零。
- 重复2-5步,直到所有检验数非正后终止,得到最优解。
例3.3 利用单纯形法解下面这个简单的规划案例:
$$ \begin{align} \text{minimize}~&f = -5x{1} - x{2}\[0.5em] \text{s.t.}~ & x{1} + x{2} \leqslant 5\ & 2x{1} + 0.5x{2} \leqslant 8\ & x{1},x{2} \geqslant {0.} \end{align} \tag{3.3.4}
$$
首先我们利用松弛变量将这个问题变成规范型:
$$ \begin{align} \text{minimize}~&f = -5x{1} - x{2}\[0.5em] \text{s.t.}~ & x{1} + x{2} + x{3} = 5\ & 2x{1} + 0.5x{2} + x{4} = 8\ & x{1},x{2}, x{3}, x{4} \geqslant {0.} \end{align} \tag{3.3.5}
$$
针对这个问题,列出如图所示的规划表:

最上面一行写下目标函数的系数,然后写下两行等式约束的系数与常数项。第一次迭代时令$z=0$, $u=f-z$,初始状况下$u$为目标函数的系数(后面会进行迭代变化),选择$u$中最大的一项也就是$5$。故选择$5$对应的元素作为入基向量,计算常数项与基向量的系数之比,发现$5/1>8/2$,选择第二行对应的松弛向量$x_4$出基。迭代后的新表格为:
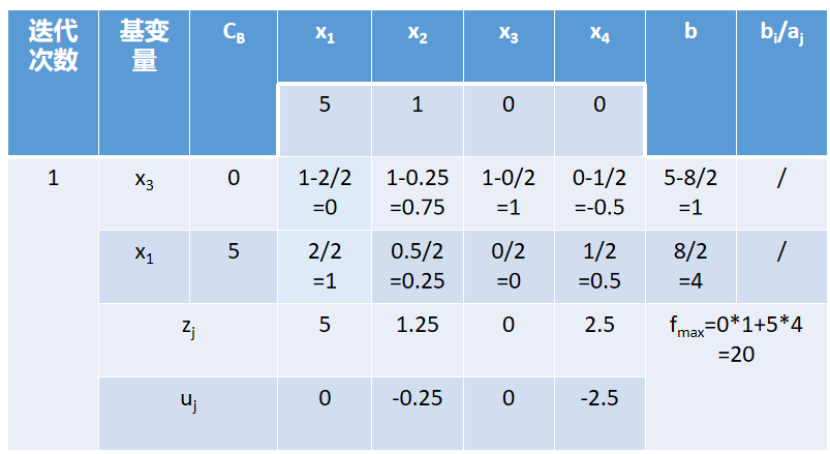
此时,将$x_4$替换为$x_1$,将$x_1$系数$5$填入表格中,原来的表格都减去第二个约束条件除以$x_1$在第二行约束中的系数$2$得到新的系数与常数项。此时,$z$等于$x_3$的系数$0$乘以第一行新约束加x_1的系数5乘以第二行新约束,得到新的z结果。$u=f-z$得到$u$的结果,所有的数都是非正数,此时迭代就结束了。常数项对应的$1,4$其实就是解,计算可以得到极值。 单纯形法的实现代码如下:
import numpy as np
def pivot(d,bn):
l = list(d[0][:-2])
jnum = l.index(max(l)) #转入编号
m = []
for i in range(bn):
if d[i][jnum] == 0:
m.append(0.)
else:
m.append(d[i][-1]/d[i][jnum])
inum = m.index(min([x for x in m[1:] if x!=0])) #转出下标
s[inum-1] = jnum
r = d[inum][jnum]
d[inum] /= r
for i in [x for x in range(bn) if x !=inum]:
r = d[i][jnum]
d[i] -= r * d[inum]
#定义基变量函数
def solve(d,bn):
flag = True
while flag:
if max(list(d[0][:-1])) <= 0: #直至所有系数小于等于0
flag = False
else:
pivot(d,bn)
def printSol(d,cn):
for i in range(cn - 1):
if i in s:
print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
else:
print("x"+str(i)+"=0.00")
print("objective is %.2f"%(-d[0][-1]))
d = np.array([[5,1,0,0,0],[1,1,1,0,5],[2,1/2,0,1,8]])
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) #基变量列表
solve(d,bn)
printSol(d,cn)
此时我们可以看到$x_1=4$,$x_2=0$,$x_3=1$,$x_4=0$,极值为$20$。
3.3.2 内点法
单纯形法之所以需要遍历所有顶点才能获得最优解,归根结底还是在于单纯形算法的搜索过程是从一个顶点出发,然后到下一个顶点,就这样一个顶点一个顶点的去搜寻最优解。单纯形算法的搜索路径始终是沿着多面体的边界的。显然,当初始点离最优点的距离很远的时候单纯形算法的搜索效率就会大大降低。
能否直接从多边形内部打进来呢?这就需要用到内点法,如图所示:
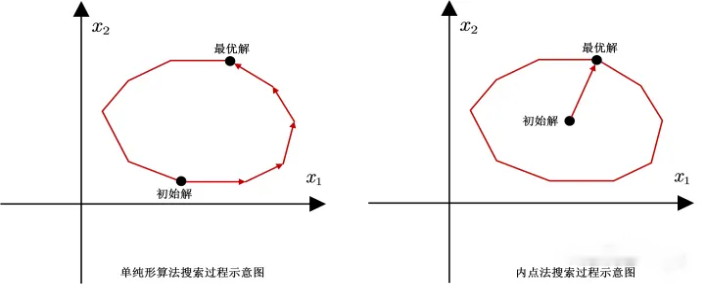
内点法的算法原理:
- 令 $k=0$,获得初始可行解$x_0$,满足如下条件: $Ax_0>b$,$x_0>b$
- 计算损失:$$r{k} = c - A^{\top}w{k}, \quad w{k} = (AX{k}^{2}A)^{-1}AX_{k}^{2}c \tag{3.3.6}$$
- 检查是否为最优解,若满足,则输出最优解;若不满足,执行下一步
- 计算搜索方向:$$d{y, k} = -\Big[ I - X{k}A^{\top}(AX{k}^{2}A)^{-1}AX{k} \Big]X{k}c = -X{k}r_{k} \tag{3.3.7}$$
- 若梯度大于$0$,表明该问题无解;若存在$0$项,则存在最优解
- 计算步长$$a{k} = \min \left.\left{ \frac{a}{-(\boldsymbol{d}{y, k}){i}} \right| (\boldsymbol{d}{y,k})_{i} < 0 \right}, \quad 0 \leqslant a \leqslant 1 \tag{3.3.8}$$
- 更新当前解$$x{k+1} = x{k} + a{k}X{k}d_{y,k} \tag{3.3.9}$$
使用内点法实现上述用例的代码如下:
import numpy as np
def Interior_Point(c,A,b):
# 当输入的c,A,b有缺失值时,输出错误原因,函数执行结束
if c.shape[0] != A.shape[1]:
print("A和C形状不匹配")
return 0
if b.shape[0] != A.shape[0]:
print("A和b形状不匹配")
return 0
# 初值的设置
x=np.ones((A.shape[1],1)) # 将x的初值设为1
v=np.ones((b.shape[0],1)) # 将v的初值设为1
lam=np.ones((x.shape[0],1)) # 将lam的初值设为1
one=np.ones((x.shape[0],1))
mu=1 # 将mu的初值设为1
n=A.shape[1]
x_=np.diag(x.flatten()) # 将x转换为对角矩阵
lam_=np.diag(lam.flatten()) # 将lam转换为对角矩阵
# 初始的F,r=F
r1=np.matmul(A,x)-b
r2=np.matmul(np.matmul(x_,lam_),one)-mu*one
r3=np.matmul(A.T,v)+c-lam
r=np.vstack((r1,r2,r3))
F=r
# 求得r1、r2、r3的初始范数
n1=np.linalg.norm(r1)
n2=np.linalg.norm(r2)
n3=np.linalg.norm(r3)
# nablaF中零矩阵和单位阵的设置
zero11=np.zeros((A.shape[0],x.shape[0]))
zero12=np.zeros((A.shape[0],A.shape[0]))
zero22=np.zeros((x.shape[0],A.shape[0]))
zero33=np.zeros((A.shape[1],A.shape[1]))
one31=np.eye(A.shape[1])
tol=1e-8 # 设置最优条件的容忍度
t=1
alpha = 0.5
while max(n1,n2,n3)>tol:
print("-----------------step",t,"-----------------")
# F的Jacobian矩阵
nablaF = np.vstack((np.hstack((zero11, zero12, A))
, np.hstack((x_, zero22, lam_))
, np.hstack((-one31, A.T, zero33))))
# F+nablaF@delta=0,解方程nablaF@delta=-r
delta = np.linalg.solve(nablaF, -r) # 解方程,求出delta的值
delta_lam = delta[0:lam.shape[0], :]
delta_v = delta[lam.shape[0]:lam.shape[0] + v.shape[0], :]
delta_x = delta[lam.shape[0] + v.shape[0]:, :]
# 更新lam、v、x、mu
alpha=Alpha(c,A,b,lam,v,x,alpha,delta_lam,delta_v,delta_x)
lam=lam+alpha*delta_lam
v=v+alpha*delta_v
x=x+alpha*delta_x
x_ = np.diag(x.flatten()) # 将x转换为对角矩阵
lam_ = np.diag(lam.flatten()) # 将lam转换为对角矩阵
mu=(0.1/n)*np.dot(lam.flatten(),x.flatten()) #更新mu的值
# 计算更新后的F
r1 = np.matmul(A, x) - b
r2 = np.matmul(np.matmul(x_, lam_), one) - mu * one
r3 = np.matmul(A.T, v) + c - lam
r = np.vstack((r1, r2, r3))
F = r
# 计算更新后F的范数
n1 = np.linalg.norm(r1)
n2 = np.linalg.norm(r2)
n3 = np.linalg.norm(r3)
t=t+1
print("x的取值",x.flatten())
print("v的取值",v.flatten())
print("lam的取值",lam.flatten())
print("mu的取值",mu)
print("alpha的取值",alpha)
z=(c.T @ x).flatten()[0]
print("值为",z)
print("##########################找到最优点##########################")
print("x的取值",x.flatten())
print('最优值为',z)
# 寻找alpha
def Alpha(c,A,b,lam,v,x,alpha,delta_lam,delta_v,delta_x):
alpha_x=[]
alpha_lam=[]
for i in range(x.shape[0]):
if delta_x.flatten()[i]<0:
alpha_x.append(x.flatten()[i]/-delta_x.flatten()[i])
if delta_lam.flatten()[i]<0:
alpha_lam.append(lam.flatten()[i]/-delta_lam.flatten()[i])
if len(alpha_x)==0 and len(alpha_lam)==0:
return alpha
else:
alpha_x.append(np.inf)
alpha_lam.append(np.inf)
alpha_x = np.array(alpha_x)
alpha_lam= np.array(alpha_lam)
alpha_max = min(np.min(alpha_x), np.min(alpha_lam))
alpha_k = min(1,0.99*alpha_max)
return alpha_k
c = np.array([-5, -1, 0,0]).reshape(-1, 1)
A = np.array([[1, 1, 1, 0], [2, 0.5, 0, 1]])
b = np.array([5, 8]).reshape(-1, 1)
# Interior_Point(c,A,b)
3.4 线性规划的建模案例
这一节我们主要学习一下线性规划的一些建模案例。
3.4.1 加工厂的加工计划
例3.4 一家加工厂使用牛奶生产A,B两种奶制品,1桶牛奶经甲机器加工12小时得到3kgA,也可以经过乙机器8小时得到4kgB,根据市场需求,生产的A、B可以全部出售并且每kgA获利24元、每kgB获利16元。现在该工厂每天获得50桶牛奶供应,所有工人的最大劳动时间之和为480小时,甲机器每天最多加工100kgA,乙机器加工不限量,请你为该工厂设计生产计划,使得每天的利润最大。
假设每天用于生产A产品的牛奶为$x{1}$桶,用于生产B产品的牛奶为$x{2}$桶,每天的利润为$z$元。问题中要优化的目标是利润,一桶牛奶给甲机器能得到3kgA,1kgA能获利24元,也就是一桶牛奶给甲能获得72元利润。同理,一桶牛奶给乙也就能获得$4\times 16=64$元利润。约束条件包括:牛奶总数只有50桶,工人劳动时间之和不能超过480小时,甲机器的加工容量上限,自变量非负。决策变量为甲乙各自使用的牛奶桶数。 根据题意建立数学模型:
$$ \begin{align} \text{minimize}~& z = 3 \times 14x{1} + 4 \times 16x{2} \[0.5em] \text{s.t.}~ & x{1} + x{2} \leqslant 50\ & 12x{1} + 8x{2} \leqslant 480\ & 3x{1} \leqslant 100\ & x{1}, x_{2} \geqslant 0 \end{align} \tag{3.4.1}
$$ 这里用python实现这个问题的代码如下:
from scipy.optimize import linprog
c=[-72,-64]
A=[[1,1],[12,8]]
b=[[50],[480]]
bounds=((0,100/3.0),(0,None))
res=linprog(c=c, A_ub=A, b_ub=b, A_eq=None, b_eq=None, bounds=bounds)
res
得到甲用$20$桶牛奶,乙用$30$桶牛奶时得到最优解$3360$。值得注意的是,自变量必须取得整数,这个约束条件作为隐含条件其实也可以加入模型中。
Checkpoint
3.4.2 油料的采购与加工计划
例3.5 某加工厂加工一种油,原料为五种油(植物油1,植物油2、非植物油1,非植物油2、非植物油3),每种油的价格、硬度如图表所示,最终生产的成品将以150英镑/吨卖出。

每个月能够提炼的植物油不超过200吨、非植物油不超过250吨,假设提炼过程中油料没有损失,提炼费用忽略不计,并且最终的产品的硬度需要在(3-6)之间(假设硬度的混合时线性的)。根据以上信息,请你为加工厂指定月采购和加工计划。 假设$x_1$,$x_2$,$x_3$,$x_4$,$x_5$分别为每月需要采购的原料油吨数,$x_6$为每个月加工的成品油吨数,由于不考虑油料损失,存在关系:
$$ x{6} = x{1} + x{2} + x{3} + x{4} + x{5}, \tag{3.4.2}
$$ 平均的硬度为:
$$ \eta = \frac{\sum\limits{i=1}^{5} w{i}x{i}}{x{6}}, \tag{3.4.3}
$$ 加上植物油重量限制和非植物油重量限制,根据题意,可以列出规划模型如下:
$$ \begin{align} \text{minimize}~& z = -110x{1} - 120x{2} - 130x{3} - 110x{4} - 115x{5} + 150x{6} \[0.5em] \text{s.t.}~ & x{1} + x{2} \leqslant 200\ & x{3} + x{4} + x{5} \leqslant 250\ & 8.8x{1} + 6.1x{2} + 2.0x{3} + 4.2x{4} + 5.0x{5} \leqslant 6x{6}\ & 8.8x{1} + 6.1x{2} + 2.0x{3} + 4.2x{4} + 5.0x{5} \geqslant 3x{6}\ & x{1} + x{2} + x{3} + x{4} + x{5} = x{6}\ & x{i} \geqslant 0, \quad i = 1, 2, \dots, 6 \end{align} \tag{3.4.4}
$$ 实现这个问题的代码如下:
c=[110,120,130,110,115,-150]
A=[[1,1,0,0,0,0],[0,0,1,1,1,0],[8.8,6.1,2.0,4.2,5.0,-6],[-8.8,-6.1,-2.0,-4.2,-5.0,3]]
b=[[200],[250],[0],[0]]
aeq=[[1,1,1,1,1,-1]]
beq=[[0]]
bounds=((0, None),(0, None),(0, None),(0, None),(0,None),(0,450))
# bounds=((0, None),(0, None),(0, None),(0, None),(0,None),(0,None))
res=linprog(c=c, A_ub=A, b_ub=b, A_eq=aeq, b_eq=beq, bounds=bounds)
我们可以看到,五种原料油的采购量分别为[159.25,40.7407,0,250,0](吨),此时总利润可以达到最大,约为$17592$英镑/月。
3.4.3 农民承包土地问题
除了scipy以外,还有没有其他工具可以求解规划问题呢?可以再关注一个工具包pulp,这个工具包专门针对线性规划问题做出了很多补充。使用pulp求解规划问题主要是三个组成部分:
LpProblem(name='NoName', sense=LpMinimize)用于定义问题与约束条件solve(solver=None, **kwargs)用于定义求解方法LpVariable(name, lowBound=None, upBound=None, cat='Continuous', e=None)用于定义决策变量
例如,如果我们要求解这样一个问题:
$$ \begin{align} \text{minimize}~& z = 2x{1} + 3x{2} + x{3} \[0.5em] \text{s.t.}~ & x{1} + 2x{2} + 4x{3} = 101\ & x{1} + 4x{2} + 2x{3} \geqslant 8\ & 3x{1} + 2x{2} \geqslant 6\ & x{i} \geqslant 0, \quad i=1,2,3 \end{align} \tag{3.4.5}
$$
使用pulp的代码如下:
import pulp as pp
# 目标函数的系数
z = [2, 3, 1]
a = [[1, 4, 2], [3, 2, 0]]
b = [8,6]
aeq = [[1,2,4]]
beq = [101]
# 确定最大最小化问题,当前确定的是最大化问题
m = pp.LpProblem(sense=pp.LpMaximize)
# 定义三个变量放到列表中
x = [pp.LpVariable(f'x{i}', lowBound=0) for i in [1, 2, 3]]
# 定义目标函数,并将目标函数加入求解的问题中
m += pp.lpDot(z, x) # lpDot 用于计算点积
# 设置比较条件
for i in range(len(a)):
m += (pp.lpDot(a[i], x) >= b[i])
# 设置相等条件
for i in range(len(aeq)):
m += (pp.lpDot(aeq[i], x) == beq[i])
# 求解
m.solve()
# 输出结果
print(f'优化结果:{pp.value(m.objective)}')
print(f'参数取值:{[pp.value(var) for var in x]}')
可以得出优化结果为$202.0$,此时的参数取值为[101.0, 0.0, 0.0]。
现在我们来看下面这个问题:
例3.6 一个农民承包了6块耕地共300亩,准备播种小麦、玉米、水果和蔬菜四种农产品,各种农产品的计划播种面积、每块土地种植不同农产品的单产收益如下表:
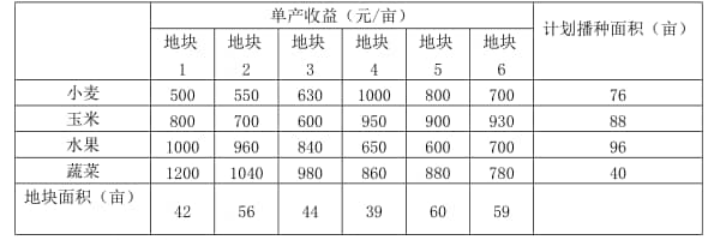 问如何安排种植计划,可得到最大收益。
问如何安排种植计划,可得到最大收益。
这是一个产销平衡的运输问题。可以建立下列的运输模型:
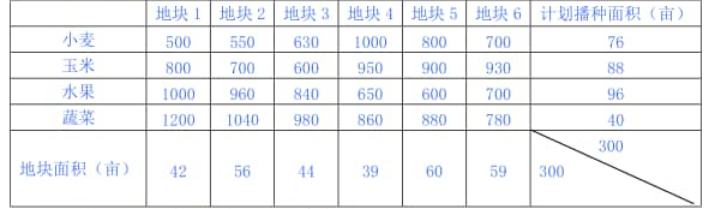 代入产销平衡的运输模板得到的种植计划方案如下表:
代入产销平衡的运输模板得到的种植计划方案如下表:
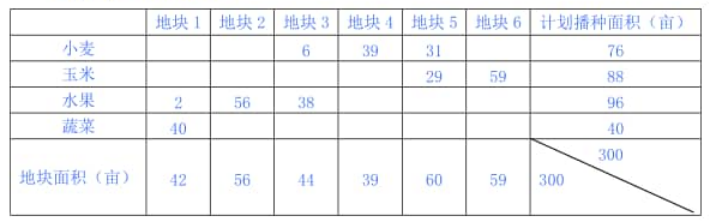 上述问题的代码如下:
上述问题的代码如下:
import pulp
import numpy as np
def transportation_problem(costs, x_max, y_max):
row = len(costs)
col = len(costs[0])
prob = pulp.LpProblem('Transportation Proble',sense=pulp.LpMaximize)
var = [[pulp.LpVariable(f'x{i}{j}',lowBound=0,cat=pulp.LpInteger) for j in range(col)] for i in range(row)]
# 转为一维
flatten = lambda x:[y for l in x for y in flatten(l)] if type(x) is list else [x]
prob += pulp.lpDot(flatten(var),costs.flatten())
for i in range(row):
prob += (pulp.lpSum(var[i]) <= x_max[i])
for j in range(col):
prob += (pulp.lpSum([var[i][j] for i in range(row)]) <= y_max[j])
prob.solve()
return {'objective':pulp.value(prob.objective),'var':[[pulp.value(var[i][j]) for j in range(col)] for i in range(row)]}
costs = np.array([[500,550,630,1000,800,700],
[800,700,600,950,900,930],
[1000,960,840,650,600,700],
[1200,1040,980,860,880,780]])
max_plant = [76,88,96,40]
max_cultivation = [42,56,44,39,60,59]
res = transportation_problem(costs, max_plant, max_cultivation)
print(f'最大值为{res["objective"]}')
print("各个变量的取值为:")
print(res['var'])
# 最大值为284230.0
# 各变量的取值为:
# [[0.0, 0.0, 6.0, 39.0, 31.0, 0.0],
# [0.0, 0.0, 0.0, 0.0, 29.0, 59.0],
# [2.0, 56.0, 38.0, 0.0, 0.0, 0.0],
# [40.0, 0.0, 0.0, 0.0, 0.0, 0.0]]
3.5 从线性规划到非线性规划
如果目标函数或约束条件中至少有一个是非线性函数时的最优化问题就叫做非线性规划问题。
3.5.1 二次规划 (Quadratic Programming, QP)
二次规划是非线性规划中的一类特殊规划问题,如果目标函数是二次函数,约束函数是线性函数时,这就是一个二次规划问题。一个有n个变量与m个限制的二次规划问题可以用以下的形式描述。首先给定:
- 一个 $n$ 维的向量$g$
- 一个$n\times n$ 维的对称矩阵$H$($x^{\top}Hx$是二次型)
- 一个$m\times n$ 维的矩阵$A$
- 一个$m$维的向量$b$
则此二次规划问题的目标即是在限制条件为$Ax \leqslant b$(不等式约束) 或$Ax = b$ (等式约束)的条件下,找一个$n$维的向量$x$ ,使得$\displaystyle f(x)=\frac{1}{2} x^{\top}H x + g^{\top}x$为最小。
可以看出QP问题的特点在于其目标函数。当$x$为一维向量时,问题变成了求二次函数的极值问题。如下图所示,二次函数具有唯一的极值,也是其最值,这是一个很理想的优化问题,能够实现快速求解,而且局部最优即为全局最优。
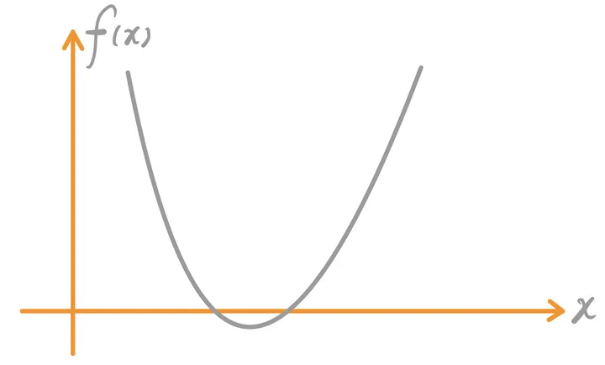
那么,当维数增大时,是否具有类似的性质呢?再此不做证明,直接给出结论:
- 如果$H$是半正定矩阵,那么$f(x)$是一个凸函数。相应的二次规划为凸二次规划问题;此时如果有局部最优解,那这个局部最优解就是全局最优解。但这个全局最小值可能是不唯一的,如下图所示。
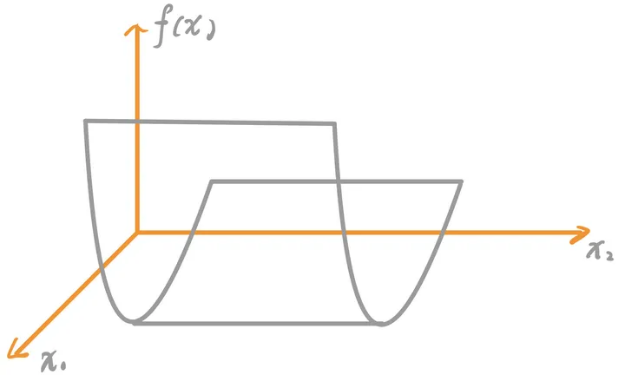
如果$H$是正定矩阵,则该问题有唯一的全局最小值,如下图所示。
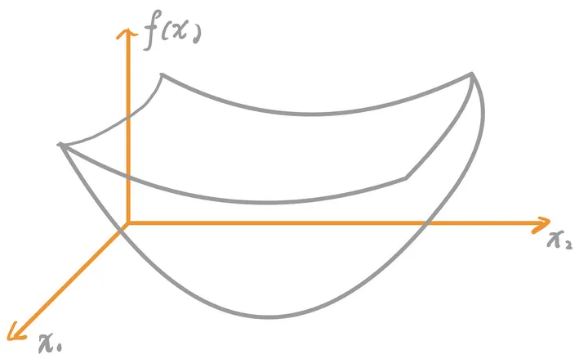
- 若$H$为非正定矩阵,则目标函数是有多个驻点和局部极小点的NP难问题。
- 如果$H=0$,二次规划问题就变成线性规划问题。
下面我们想一下为什么要引入二次规划,以及为什么二次规划问题被写成了上面那种标准形式。首先要明确两个概念,维度是自变量的个数,次数是自变量最高的阶数,两个不能弄混。我们解决问题的思路是将不熟悉的问题,转换成熟悉的问题。其中优化轨迹点是不熟悉的问题,但是求解多项式的极值是熟悉的问题。因此我们希望将复杂问题转换为一个与多项式求极值类似的问题。而求解多项式极值也要看多项式的次数,如果是一次,那就是直线,没什么好讨论的。如果是二次,那函数将有唯一的极值,也是最值,这是我们最想看到的。如果超过2次,那问题就复杂了。
多项式求极值是二维空间的问题,只有$x$和$y$两个变量。而运动规划的优化问题是高维的。高维空间的优化问题是十分复杂的,我们如果将其转换为一个类似于我们熟悉的多项式求极值问题,我们当然希望选择对优化来说最理想的二次。如果问题的维度也高,次数也高,就很难求解了。于是我们希望将问题转化为这样一个高维空间中,类似于二次函数求极值的问题,所以目标函数这样定义:
$$ f(x) = x^{\top}Hx + g^{\top}x. \tag{3.5.1}
$$
3.5.2 非线性规划的求解
类比线性规划的基本形式,我们把所有的线性方程约束中系数做成系数矩阵$A{\text{eq}}$,等号右边的常数作为列向量$b{\text{eq}}$;线性不等式约束中的系数矩阵$A$和不等号右边的常数$b$,为了方便起见通常将不等式统一为小于等于;变量$x$在向量$l{b}$到$u{b}$之间取值;非线性不等式和非线性方程分别用$C(x)$和$C_{\text{eq}}(x)$,则线性规划的标准形式如下所示:
$$ \begin{align} \text{minimize}~& f(x) \[0.5em] \text{s.t.}~ & Ax \leqslant b\ & C(x) \leqslant 0\ & A{\text{eq}}x = b{\text{eq}}\ & C{\text{eq}}(x) = 0\ & l{b} \leqslant x \leqslant u_{b} \end{align} \tag{3.5.2}
$$ 我们仍然将问题统一为函数极小值问题,不等约束统一为小于等于。如果原问题是最大值或者有大于等于,那就乘$-1$进行取反即可。
注意:非线性规划中只要破坏了等式约束、不等约束和目标函数当中任何一个的线性就可以说是一个非线性规划。仅仅破坏一条问题的求解难度会上来很多。
从线性到非线性,多元函数可能初来乍到的同学并不一定理解。在高中我们说,函数是从一个集合(定义域)到另一个集合(值域)的一一对应的映射,那现在多元函数?不就变成多个集合到一个集合的映射了嘛?这,怎么也能叫一一对应呢?诶,这个时候你就注意了,多元函数仍然是一个集合到另一个集合的映射,只不过自变量的集合不是数集,而是点集,或者说是$n$维空间里面向量的集合。
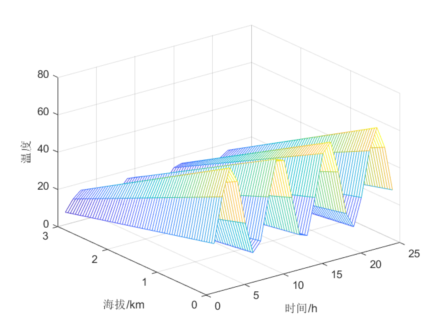
举个例子,比如说一个地方的温度与海拔,海拔越高温度就越低,另外一天24小时的温度是中午高早晚低还呈现周期变化,那么气温就受到海拔和时间两个因素影响。我们不妨假定,这个地方的温度规律为$\displaystyle T = (40 - 25 \cos t)\left( 1 - \frac{h}{4} \right)$,可以做出一个如图2.4所示的曲面图:
如果高中学过导数的同学可能知道,一元函数求极值的一个方法就是求导导数为$0$。对于多元函数也类似,如果是无约束就只是给了一个多元函数求极值,只需要针对每个变量分别求导数(我们把这个过程叫做求偏导),所有偏导为$0$解方程组得到的就是极值点的候选解。当然,我们有可能解出来的是$x_3=0$的这种极值解,这种情况下我们会通过二阶导数的符号去进一步判定。
注意:在求对某一个变量的偏导数的时候通常把其他变量视作常数,我们把这种策略叫主元策略(我想在中学阶段老师应该讲过)。
当我们碰上了有约束条件下的非线性函数求极值的时候,我们通常使用 Lagrange 法。例如,对于广义的含等式条件(先暂时只考虑等式问题)的极值问题:
$$ \begin{align} \text{minimize}~& f(x) \[0.5em] \text{s.t.}~ & C_{i}(x) = 0, \quad i=1,\dots,n \end{align} \tag{3.5.3}
$$ 我们通过引入$n$个称之为Lagrange 乘子的常数把原问题改写为新的函数:
$$ \min L (x, \lambda) = f(x) + \sum\limits{i=1}^{n} \lambda{i}C_{i}(x). \tag{3.5.4}
$$ 接下来就像解无约束极值一样对每个$x$和乘子求偏导即可解决问题。而当我们在问题中考虑不等条件,那么这个问题的求解策略其实类似,我们称其为KKT条件。对于问题
$$ \begin{align} \text{minimize}~& f(x) \[0.5em] \text{s.t.}~ & h(x) = 0\ & g(x) \leqslant 0, \end{align} \tag{3.5.5}
$$ 我们分别引入两个不同乘子,函数$L$将在$x$取得极值当且仅当它在下面的问题中取得极值:
$$ \begin{align} \text{minimize}~& L(x, \lambda, \mu) = f(x) + \lambda h(x) + \mu g(x) \[0.5em] \text{s.t.}~ & \frac{ \partial L }{ \partial x } = 0\ & \lambda \ne 0\ & \mu \geqslant 0\ & \mu g(x) = 0\ & h(x) = 0\ & g(x) \leqslant 0 \end{align} \tag{3.5.6}
$$ 当然,如果想求的不是一个精确解而是一个近似的数值解,那么我们的方法同样有很多。除了在下一章中会介绍的一些数值方法外,Monte Carlo模拟几乎是用的最广泛的一种。
3.6 非线性规划的建模案例
在这一节中我们会看到一些非线性规划的建模案例。
3.6.1 商品选购优化
现在有三种产品,产品的收益与成本的关系分别为:
$$ \begin{cases} P{1} = 3 + 0.004x{1} + 0.0025x{1}^{2}, & 100 \leqslant x{1} \leqslant 200\ P{2} = 4 - 0.02x{2} + 0.0033 x{2}^{2}, & 150 \leqslant x{2} \leqslant 250\ P{3} = 6 + 0.0015x{3}, & 150 \leqslant x_{3} \leqslant 300 \end{cases} \tag{3.6.1}
$$ 假如你的手中有七百万作为本金,你应该如何投资使你的总收益最大?
这个例子也很简单,我们的约束条件无非只有$x{1} + x{2} + x_{3} \leqslant 700$,将目标函数写出来:
def func(x):
return 10.5+0.3*x[0]+0.32*x[1]+0.32*x[2]+0.0007*x[0]**2+0.0004*x[1]**2+0.00045*x[2]**2
cons=({'type':'eq','fun':lambda x: x[0]+x[1]+x[2]-700})
b1,b2,b3=(100,200),(120,250),(150,300)
x_0=np.array([100,200,400])
res=minimize(func,x_0,method='SLSQP',constraints=cons,bounds=(b1,b2,b3))
print(res)
from sko.GA import GA
def func(x):
return 10.5+0.3*x[0]+0.32*x[1]+0.32*x[2]+0.0007*x[0]**2+0.0004*x[1]**2+0.00045*x[2]**2
cons=lambda x: x[0]+x[1]+x[2]-700
b1,b2,b3=(100,200),(120,250),(150,300)
ga=GA(func=func,n_dim=3,size_pop=500,max_iter=500,constraint_eq=[cons],lb=[100,120,150],ub=[200,250,300])
best_x,best_y=ga.run()
print("best x:\n",best_x,"\nbest_y:\n",best_y)
3.6.2 工地选址
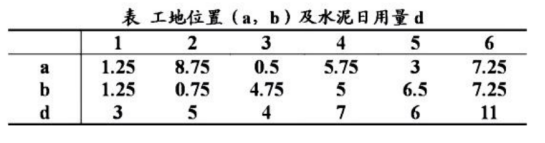
某公司有$6$个建筑工地要开工,每个工地的位置(用平面坐标系$a,b$表示,距离单位:千米)及水泥日用 量$d$(吨)由下表给出。规划设立两个料场位于$A$,$B$,日储量各为20吨。假设从料场到工地之间均有 直线道路相连,试确定料场的位置,并制定每天的供应计划,即从$A$,$B$两料场分别向各工地运送多少吨水泥,使总的吨千米数最小。
我们可以分析这一个问题。我们说,规划问题的核心有三样:决策变量,目标函数和约束条件。
决策变量包括哪些?首先两个料场的坐标未知吧,坐标有横纵坐标于是这就有了四个变量;两个料场到六个工地$12$条线路上的运输量也未知吧,于是这就又来了12个变量,一共是$16$个。距离可以用 Euclid 距离来计算,所以可以写出一个目标函数:
def tkm(x):
s=0
j=3
a=[1,25,8.75,0.5,5.75,3,7.25]
b=[1.25,0.75,4.75,5,6.5,7.25]
for i in range(6):
s+=x[j+1]*np.sqrt((x[0]-a[i])**2+(x[1]-b[i])**2)+x[j+2]*np.sqrt((x[2]-a[i])**2+(x[3]-b[i])**2)
j+=2
return s
这里的$x$是一个$16$维的向量,前四维表示两个料场的坐标,后面$12$个分别表示料场$1$到六个工地的运输量和料场$2$到六个工地的运输量。运输量之间需要满足限制。首先,料场$1$到六个工地的运输量之和与料场2到六个工地的运输量之和都不能超过$20$吨,这是存量的限制;其次,每个工地从两个料场获取的运输量之和得等于自己的一个需求量。这里其实如果把每个工地的限制看作一个大于等于也是说得通的,但我们这里为了求解方便把这一部分看作等式约束也是没问题的。
$$ \begin{align} \text{minimize}~& \sum\limits{i=1}^{6} \sum\limits{j=1}^{2} m{i,j}\sqrt{ (x{j} - a{i})^{2} + (y{j} - b{i})^{2} } \[0.5em] \text{s.t.}~ & \sum\limits{i=1}^{6} m{i,j} \leqslant 20, \quad j=1,2\ & \sum\limits{j=1}^{2} m{i,j} = d{i}, \quad i=1,2,\dots,6\ & m{i,j} \geqslant 0, \quad \forall i,j\ & x{1}, x{2}, y{1}, y_{2} \geqslant 0 \end{align} \tag{3.6.2}
$$ 这样我们就可以写出等式约束和不等式约束:
lccons=({'type':'eq','fun':lambda x: x[4]+x[10]-3},
{'type':'eq','fun':lambda x: x[5]+x[11]-5},
{'type':'eq','fun':lambda x: x[6]+x[12]-7},
{'type':'eq','fun':lambda x: x[7]+x[13]-7},
{'type':'eq','fun':lambda x: x[8]+x[14]-6},
{'type':'eq','fun':lambda x: x[9]+x[15]-11},
{'type':'ineq','fun':lambda x: x[4]+x[5]+x[6]+x[7]+x[8]+x[9]-20},
{'type':'ineq','fun':lambda x: x[10]+x[11]+x[12]+x[13]+x[14]+x[15]-20})
b=((0,None),(0,None),(0,None),(0,None),(0,None),(0,None),(0,None),(0,None),(0,None),(0,None),(0,None),(0,None),(0,None),(0,None),(0,None),(0,None))
x_0=np.ones((16,1))
res=minimize(tkm,x_0,method='SLSQP',constraints=lccons,bounds=b)
print(res.x)
当你去运行这个函数,求得的最小吨千米数为$69.6134$,两个料场的坐标分别为$(3,6.5)$和$(0.5,4.75)$。
3.6.3 职称晋级与评审规划
某单位在考虑本单位职工的升级调薪方案时要求相关部门遵守以下的规定:
- 年工资总额不超过$1500000$元;
- 每级的人数不超过定编规定的人数;
- II、III级的升级面尽可能达到现有人数的$20\%$;
- III级不足编制的人数可录用新职工,又I级职工中$10\%$要退休。 相关资料汇总于表中,请为单位领导拟定一个满足要求的调资方案。
| 等级 | 工资(元/年) | 现有人数 | 编制人数 |
|---|---|---|---|
| I | $50000$ | $10$ | $12$ |
| II | $30000$ | $12$ | $15$ |
| III | $2000$ | $15$ | $15$ |
| 合计 | $37$ | $42$ |
为了考虑选取最优的调资方案,需要考虑三个约束条件,显然前两个约束条件为刚性约束,而第三个约束条件为柔性约束。分别建立目标约束:设由II晋升为I的人数为$x_{1}$,由III晋升为II的人数为$x_2$,招聘为III的人数为$x_3$,$d_n^-$为未满误差,$d_n^+$为过盈误差,其中$n=1,2,3,4,5$。 为保证调资后的年工资预算仍在指标范围内:
$$ \begin{align} \text{minimize}~& d{1}^{+} \[0.5em] \text{s.t.}~ & 50000(9 + x{1}) + 30000(12 - x{1}) + 20000(15 - x{2} + x{3}) + d{1}^{-} - d_{1}^{+} = 1500000 \end{align} \tag{3.6.3}
$$ 每一级人数不超过定编规定人数:
$$ \begin{align} \text{minimize}~& d{2}^{+} + d{3}^{+} + d{4}^{+} \[0.5em] \text{s.t.}~ & 9 + x{1} + d{2}^{-} - d{2}^{+} = 12\ & 12 - x{1} + x{2} + d{3}^{-} - d{3}^{+} = 15\ & 15 - x{2} + x{3} + d{4}^{-} - d{4}^{+} = 15\ \end{align} \tag{3.6.4}
$$ II,III的升级面尽量达到现有人数的$20\%$:
$$ \begin{align} \text{minimize}~& d{5}^{-} - d{5}^{+} + d{6}^{-} - d{6}^{+} \[0.5em] \text{s.t.}~ & x{1} + d{5}^{-} - d{5}^{+} = 3\ & x{2} + d{6}^{-} - d{6}^{+} = 3 \end{align} \tag{3.6.5}
$$ 最终得到的目标函数与约束如下:
$$ \begin{align} \text{minimize}~& p{1}\cdot(d{1}^{+}) + p{2}\cdot(d{2}^{+} + d{3}^{+} + d{4}^{+}) + p{3}\cdot(d{5}^{-} - d{5}^{+} + d{6}^{-} - d{6}^{+}) \[0.5em] \text{s.t.}~ & 50000(9 + x{1}) + 30000(12 - x{1}) + 20000(15 - x{2} + x{3}) + d{1}^{-} - d{1}^{+} = 1500000\ & 9 + x{1} + d{2}^{-} - d{2}^{+} = 12\ & 12 - x{1} + x{2} + d{3}^{-} - d{3}^{+} = 15\ & 15 - x{2} + x{3} + d{4}^{-} - d{4}^{+} = 15\ & x{1} + d{5}^{-} - d{5}^{+} = 3\ & x{2} + d{6}^{-} - d{6}^{+} = 3 \end{align} \tag{3.6.6}
$$ 其中$p{1}, p{2}, p_{3}$是权重值。实现这个问题的代码如下:
from scipy.optimize import linprog
c=np.array([0,0,0,0,1,0,1,0,1,0,1,-1,1,-1,1])
Aeq=np.array([[20000,10000,20000,-1,1,0,0,0,0,0,0,0,0,0,0],
[1,0,0,0,0,-1,1,0,0,0,0,0,0,0,0],
[-1,1,0,0,0,0,0,-1,1,0,0,0,0,0,0],
[0,-1,1,0,0,0,0,0,0,-1,1,0,0,0,0],
[1,0,0,0,0,0,0,0,0,0,0,-1,1,0,0],
[0,1,0,0,0,0,0,0,0,0,0,0,0,-1,1]])
beq=np.array([[300000,3,3,0,3,3]])
bounds=[(0,10)]*15
res=linprog(c,None,None,Aeq,beq,bounds)
res
3.7 整数规划与指派问题
3.7.1 整数规划的基本概念
离散和连续是一对重要的概念。这一对概念其实非常好理解:比如说,连续的变量取值是连续的实数,取值可以是任意的浮点数(小数),但离散变量取值是不连续的,是有间隔的。离散量的取值往往是整数,也可能是有限的取值。
离散优化的例子其实也很简单,如果把前面的线性规划或者非线性规划当中加上一条约束:自变量取整数,这个问题就开始有意思了。可能最优解是一个全浮点数,但加上整数约束以后究竟在哪个整数点上取到最优解那还真说不好,你如果用枚举的方式去解那复杂度是成倍上涨。我们想,一定有更快的求解策略。
另一类离散优化的典型例子是匹配问题和组合优化问题,比如有$100$个人匹配$100$项任务,百配百就有五千种匹配模式。而这么多的匹配模式中究竟哪一个是最优解呢?那就得在五千种匹配模式中搜索,变量就是某一个人是否匹配某一项任务,取值只能是${0,1}$。所以这就是一种离散优化。下面我们也会对这类问题进行介绍。
3.7.2 分支定界法
同单纯形法与Monte Carlo法之于线性规划,解整数规划的基础原理其实更多。最典型的两种算法就是分支定界法和割平面法。
分支定界法是一种经典的搜索算法,这里把它用在规划当中主要是为了对上下界进行搜索。分支定界本质上是构造一棵搜索树进行上下界搜索,它会把问题的搜索空间组织成一棵树,而分支就是从根出发将原始问题按照整数约束去分支为左子树和右子树,通过不断检查子树的上下界去搜索最优解的过程。 我们举一个例子:
例3.7 求规划的最优解。
首先我们忽略取值${0,1}$这个条件,把它就当做一个取值范围$[0,1]$之间的线性规划去做,它肯定是有最优解的,这毋庸置疑。现在,我们从$x_3$开始分支,分别按取$0$和取$1$去对原始问题进行划分。如果$x_3$取值为$1$,那么原始问题变成了$7x_1+8x_2\leqslant 7$的条件下最大化$x_1+x_2+1$;如果取值为$0$那么原始问题变成了$7x_1+8x_2\leqslant 14$的条件下最大化$x_1+x_2$。然后我们分别计算两边的最优解,两边都可能存在最优整数解于是对这两种情况再进行划分。每划分一次我们就会对同一层的子问题求解对应的线性规划(把整数条件换成区间条件)观察谁最小谁可分,到最后遍历完成就得到了最优解。如图2.6所示:
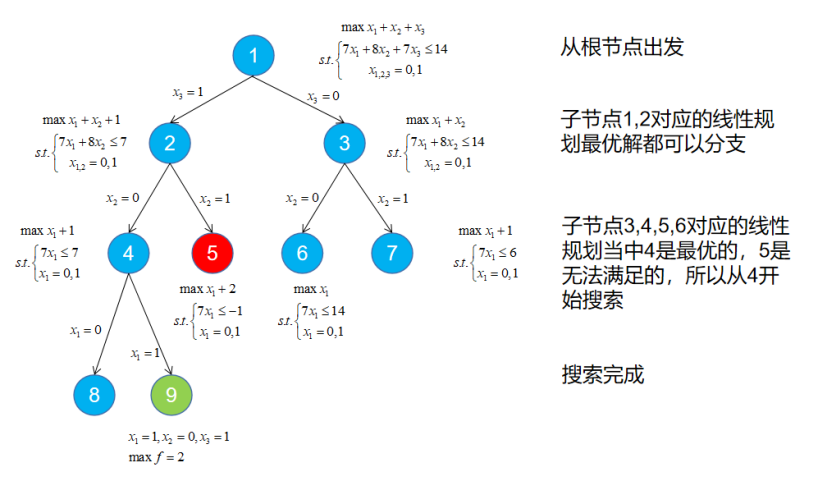
注意:我们每经过一层就会更新一个线性规划的最优解(也可以叫松弛解),在根节点我们将它设置为负无穷,而在子节点中只要能够比上一次的最优解更优我们就会更新这个最优解。比如说在第三层,节点4的最优解$2$就是最优,而节点6的最优解$1$和节点7的最优解$1.8571$再怎么分不会比节点4更优,所以我们下一步只对节点4分支并按照这一分支为子问题定界。
import math
from scipy.optimize import linprog
import sys
def integerPro(c, A, b, Aeq, beq, t=1.0E-8):
res = linprog(c, A_ub=A, b_ub=b, A_eq=Aeq, b_eq=beq)
bestVal = sys.maxsize # 很大一个数
bestX = res.x
if not (type(res.x) is float or res.status != 0):
bestVal = sum([x * y for x, y in zip(c, bestX)])
if all(((x - math.floor(x)) <= t or (math.ceil(x) - x) <= t) for x in bestX):
return bestVal, bestX
else:
ind = [i for i, x in enumerate(bestX) if (x - math.floor(x)) > t and (math.ceil(x) - x) > t][0]
newCon1 = [0] * len(A[0])
newCon2 = [0] * len(A[0])
newCon1[ind] = -1
newCon2[ind] = 1
newA1 = A.copy()
newA2 = A.copy()
newA1.append(newCon1)
newA2.append(newCon2)
newB1 = b.copy()
newB2 = b.copy()
newB1.append(-math.ceil(bestX[ind]))
newB2.append(math.floor(bestX[ind]))
r1 = integerPro(c, newA1, newB1, Aeq, beq)
r2 = integerPro(c, newA2, newB2, Aeq, beq)
if r1[0] < r2[0]:
return r1
else:
return r2
if __name__ == '__main__':
c = [3, 4, 1]
A = [[-1, -6, -2], [-2, 0, 0]]
b = [-5, -3]
Aeq = [[0, 0, 0]]
beq = [0]
print(integerPro(c, A, b, Aeq, beq))
3.7.3 指派问题与匈牙利法
0-1规划是整数规划中最特殊的一种。它的限制不仅仅是要求变量是整数,而且只能是0或1,故而名曰0-1规划。事实上,在数学建模竞赛当中,0-1规划可以说是最常见的整数规划,是学习的重点。指派问题又是怎么一回事呢?我们可以看到这样一个例子:
例3.8 现在有4个人${A,B,C,D}$可以做四项工作${1,2,3,4}$,他们每个人只能做一项工作,所需要的时间按照表2.3给出:
| 时间 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 6 | 7 | 11 | 2 |
| B | 4 | 5 | 9 | 8 |
| C | 3 | 1 | 10 | 4 |
| D | 5 | 9 | 8 | 2 |
我们把四个人与$4$项工作对应的$4\cdot4=16$项安排作为决策变量,变量取值为${ 0,1 }$,表示某个人是否执行某项工作。一个人只能做一项工作,一项工作也只能一个人来做,比如对$A$而言,$A$如果做了$2$就不能做$1,3,4$,所以$A$匹配的四个变量只能有一个是$1$其余三个都是$0$。同样地,对任务$2$而言如果它被安排给了$A$那么$B,C,D$也都不能去做,所以任务$2$匹配的四个变量也只能一个是$1$其余三个是$0$。由此,我们给出定义:
$$ \begin{align} \text{minimize}~& f(x) = \sum\limits{i=1}^{4} \sum\limits{j=1}^{4} x{i,j}T{i,j} \[0.5em] \text{s.t.}~ & \sum\limits{i=1}^{4} x{i,j} = 1, \quad \forall j\ & \sum\limits{j=1}^{4} x{i,j} = 1, \quad \forall i\ & x_{i,j} \in { 0,1 }, \quad \forall i,j. \end{align} \tag{3.7.1}
$$ 指派问题和0-1规划的解法可以从matlab的整数规划函数中进行约束,但还有一种经典的算法可以解0-1规划。这个方法被称作匈牙利法。匈牙利法的操作比较有趣,对于时间排布表,首先将每行减去当前行的最小值,然后将每一列的值减去当前列的最小值。接下来一步比较有趣,需要用最少的水平线和竖直线覆盖所有的$0$项。如果线条总数为$4$那么算法停止,给出指派方案;如果少于4条那么则计算没有被覆盖的最小值,将没有被覆盖的每行减去最小值,被覆盖的每列加上最小值,然后重新进行覆盖。整个过程如图2.7:

from scipy.optimize import linear_sum_assignment
import numpy as np
T=np.array([[25,29,31,42],[39,38,26,20],[34,27,28,40],[24,42,36,23]])
row_ind,col_ind=linear_sum_assignment(T)
print(row_ind)
print(col_ind)
print(T[row_ind,col_ind])
print(T[row_ind,col_ind].sum())
3.8 使用Scipy和Cvxpy解决规划问题
Python 提供了多种库和工具来解决线性规划问题,如 scipy、cvxpy等。本节将介绍如何使用这些库来解决线性规划问题,并给出示例代码和运行结果。
3.8.1 使用scipy求解函数优化问题
在 scipy.optimize 模块中,提供了多种用于非线性规划问题的方法,适用于不同类型的问题:
brent(): 适用于单变量无约束优化问题,结合了Newton 法和二分法。fmin(): 适用于多变量无约束优化问题,采用单纯形法,只需利用函数值,无需函数的导数或二阶导数。leastsq(): 用于解决非线性最小二乘问题,用于求解非线性最小二乘拟合问题。minimize(): 适用于约束优化问题,利用 Lagrange 乘子法将约束优化问题转化为无约束优化问题。
minimize(fun, x_0[, args, method, jac, hess, ...]):用于对一个或多个变量的标量函数进行最小化。
对于无约束问题优化算法:
method='CG': 非线性共轭梯度算法,只能处理无约束优化问题,需要使用一阶导数函数。method='BFGS': 拟 Newton 法,只能处理无约束优化问题,需要使用一阶导数函数。BFGS 算法性能良好,是无约束优化问题的默认算法。method='Newton-CG': 截断 Newton 法,只能处理无约束优化问题,需要使用一阶导数函数,适合处理大规模问题。method='dogleg': Dog-leg 信赖域算法,需要使用梯度和 Hessian 矩阵(必须正定),只能处理无约束优化问题。method='trust-ncg': 采用 Newton 共轭梯度信赖域算法,需要使用梯度和 Hessian 矩阵(必须正定),只能处理无约束优化问题,适合大规模问题。method='trust-exact': 求解无约束极小化问题的信赖域方法,需要梯度和 Hessian 矩阵(不需要正定)。method='trust-krylov': 使用 Newton-GLTR 信赖域算法,需要使用梯度和 Hessian 矩阵(必须正定),只能处理无约束优化问题,适合中大规模问题。
对于边界约束条件问题优化算法:
method='Nelder-Mead': 下山单纯形法,可以处理边界约束条件(决策变量的上下限),只使用目标函数,不使用导数函数或二阶导数,具有较强的鲁棒性。method='L-BFGS-B': 改进的 BFGS 拟Newton 法,"L" 指有限内存,"B" 指边界约束,可以处理边界约束条件,需要使用一阶导数函数。L-BFGS-B 算法性能良好,内存消耗小,适合处理大规模问题,是边界约束优化问题的默认算法。method='Powell': 改进的共轭方向法,可以处理边界约束条件(决策变量的上下限)。method='TNC': 截断Newton 法,可以处理边界约束条件。
对于带有约束条件问题优化算法:
method='COBYLA': 线性近似约束优化方法,通过线性逼近目标函数和约束条件来处理非线性问题。只使用目标函数,不需要导数或二阶导数值,可以处理约束条件。method='SLSQP': 序贯最小二乘规划算法,可以处理边界约束、等式约束和不等式约束条件。SLSQP 算法性能良好,是带有约束条件优化问题的默认算法。method='trust-constr': 信赖域算法,通用的约束最优化方法,适合处理大规模问题。
下面给出了一些利用 scipy.optimize 模块进行求解的代码示例:
from scipy.optimize import brent, fmin, fmin_ncg, minimize
import numpy as np
# 1. Demo1:单变量无约束优化问题(Scipy.optimize.brent)
def objf(x): # 目标函数
fx = x**2 - 8*np.sin(2*x+np.pi)
return fx
xIni = -5.0
xOpt= brent(objf, brack=(xIni,2))
print("xIni={:.4f}\tfxIni={:.4f}".format(xIni,objf(xIni)))
print("xOpt={:.4f}\tfxOpt={:.4f}".format(xOpt,objf(xOpt)))
def objf2(x): # Rosenbrock benchmark function
fx = 100.0 * (x[0] - x[1] ** 2.0) ** 2.0 + (1 - x[1]) ** 2.0
return fx
xIni = np.array([-2, -2])
xOpt = fmin(objf2, xIni)
print("xIni={:.4f},{:.4f}\tfxIni={:.4f}".format(xIni[0],xIni[1],objf2(xIni)))
print("xOpt={:.4f},{:.4f}\tfxOpt={:.4f}".format(xOpt[0],xOpt[1],objf2(xOpt)))
#目标函数:
def func(args):
fun = lambda x: 60 - 10*x[0] - 4*x[1] + x[0]**2 + x[1]**2 - x[0]*x[1]
return fun
#约束条件,包括等式约束和不等式约束
def con(args):
cons = ({'type': 'eq', 'fun': lambda x: x[0]+x[1]-8})
return cons
# 解决问题是:当x_1+x_2=8时,求解函数60-10x_1-4x_2+x_1^2+x_2^2-x_1x_2的极小值
if __name__ == "__main__":
args = ()
args1 = ()
cons = con(args1)
x_0 = np.array((2.0, 1.0)) #设置初始值,初始值的设置很重要,很容易收敛到另外的极值点中,建议多试几个值
#求解#
res = minimize(func(args), x_0, method='SLSQP', constraints=cons)
print(res)
def objF4(x): # 定义目标函数
a, b, c, d = 1, 2, 3, 8
fx = a*x[0]**2 + b*x[1]**2 + c*x[2]**2 + d
return fx
# 定义约束条件函数
def constraint1(x): # 不等式约束 f(x)>=0
return x[0]** 2 - x[1] + x[2]**2
def constraint2(x): # 不等式约束 转换为标准形式
return -(x[0] + x[1]**2 + x[2]**3 - 20)
def constraint3(x): # 等式约束
return -x[0] - x[1]**2 + 2
def constraint4(x): # 等式约束
return x[1] + 2*x[2]**2 -3
# 定义边界约束
b = (0.0, None)
bnds = (b, b, b)
# 定义约束条件
con1 = {'type': 'ineq', 'fun': constraint1}
con2 = {'type': 'ineq', 'fun': constraint2}
con3 = {'type': 'eq', 'fun': constraint3}
con4 = {'type': 'eq', 'fun': constraint4}
cons = ([con1, con2, con3,con4]) # 3个约束条件
# 求解优化问题
x_0 = np.array([1., 2., 3.]) # 定义搜索的初值
res = minimize(objF4, x_0, method='SLSQP', bounds=bnds, constraints=cons)
print("Optimization problem (res):\t{}".format(res.message)) # 优化是否成功
print("xOpt = {}".format(res.x)) # 自变量的优化值
print("min f(x) = {:.4f}".format(res.fun)) # 目标函数的优化值
def objF5(x,args): # 定义目标函数
a,b,c,d = args
fx = lambda x: a*x[0]**2 + b*x[1]**2 + c*x[2]**2 + d
return a*x[0]**2 + b*x[1]**2 + c*x[2]**2 + d
def constraint1(): # 定义约束条件函数
cons = ({'type': 'ineq', 'fun': lambda x: (x[0]**2 - x[1] + x[2]**2)}, # 不等式约束 f(x)>=0
{'type': 'ineq', 'fun': lambda x: -(x[0] + x[1]**2 + x[2]**3 - 20)}, # 不等式约束 转换为标准形式
{'type': 'eq', 'fun': lambda x: (-x[0] - x[1]**2 + 2)}, # 等式约束
{'type': 'eq', 'fun': lambda x: (x[1] + 2*x[2]**2 - 3)}) # 等式约束
return cons
# 定义边界约束
b = (0.0, None)
bnds = (b, b, b)
# 定义约束条件
cons = constraint1()
args1 = (1,2,3,8) # 定义目标函数中的参数
# 求解优化问题
x_0 = np.array([1., 2., 3.]) # 定义搜索的初值
res1 = minimize(objF5, x_0=x_0, args=[1,2,3,8], method='SLSQP', bounds=bnds, constraints=cons)
print("Optimization problem (res1):\t{}".format(res1.message)) # 优化是否成功
print("xOpt = {}".format(res1.x)) # 自变量的优化值
print("min f(x) = {:.4f}".format(res1.fun)) # 目标函数的优化值
3.8.2 使用cvxpy求解函数优化问题
CVXPY 是一种用于凸优化问题的 Python 嵌入式建模语言。它允许您以遵循数学的自然方式表达您的问题,而不是求解器要求的限制性标准形式
| 求解状态 | 含义 |
|---|---|
| OPTIMAL | 最优解 |
| INFEASIBLE | 不可行 |
| UNBOUNDED | 无界 |
| OPTIMAL_INACCURATE | 不精确 |
| INFEASIBLE_INACCURATE | 不精确 |
| UNBOUNDED_INACCURATE | 不精确 |

CVXPY 的变量类型
变量可以是标量、向量以及矩阵 cvxpy 中可以做常数使用的有:
- NumPy
ndarrays - NumPy
matrices - SciPy sparse matrices
CVXPY 的约束可以使用 ==, <=,>= ,不能使用< ,>。也不能使用0 <= x <= 1 or x == y == 2。
parameters可以理解为参数求解问题里的一个常数,可以是标量、向量、矩阵。在没有求解问题前(调用类xxx.solve()),其允许你改变其值。
例1
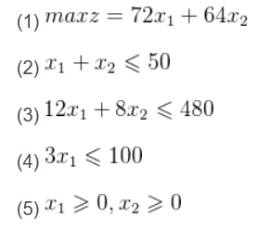
解决这个问题的代码如下
import cvxpy as cp
import numpy as np
coef = np.array([72, 64])#输入目标函数系数
left = np.array([[1, 1], [12, 8], [3, 0]])#输入约束条件系数
right = np.array([50, 480, 100])#输入约束条件上限值
x = cp.Variable(2)#构造决策变量
obj = cp.Maximize(coef @ x)#构造目标函数
cons = [x >= 0, left @ x <= right]#构造约束条件
prob = cp.Problem(obj, cons)#构建模型
prob.solve(solver='GUROBI')#模型求解
print("最优值:", prob.value)
print("最优解:", x.value)
print("剩余牛奶:", right[0] - sum(left[0] * x.value))
print("剩余劳动时间:", right[1] - sum(left[1] * x.value))
print("A1剩余加工能力:", right[2] - sum(left[2] * x.value))
例2

解决这个问题的代码如下
import cvxpy as cp
import numpy as np
#输入目标函数系数
coef = np.array([160, 130, 220, 170,
140, 130, 190, 150,
190, 200, 230])
#输入约束条件系数
left = np.array([[1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0],
[0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0],
[0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1],
[0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0]])
right_min = np.array([30, 70, 10, 10])#输入约束条件下限值
right_max = np.array([80, 140, 30, 50])#输入约束条件上限值
x = cp.Variable(11)#构造决策变量
obj = cp.Minimize(coef @ x)#构造目标函数
#构造约束条件
cons = [x >= 0,
left @ x <= right_max,
left @ x >= right_min,
cp.sum(x[0:4]) == 50,
cp.sum(x[4:8]) == 60,
cp.sum(x[8:11]) == 50]
prob = cp.Problem(obj, cons)#构建模型
prob.solve(solver="GUROBI")#模型求解
print("管理费用最小值为:", prob.value)
print("最优分配方案为:", x.value)
例3

解决这个问题的代码如下
import cvxpy as cp
import numpy as np
coef = np.array([2, 3, 4])#输入目标函数系数
left = np.array([[1.5, 3, 5], [280, 250, 400]])#输入约束条件系数
right = np.array([600, 60000])#输入输入约束条件上限值
x = cp.Variable(3, integer=True)#创建决策变量,并且为整数
obj = cp.Maximize(coef @ x)#构造目标函数
cons = [x >= 0, left @ x <= right]#构造约束条件
prob = cp.Problem(obj, cons)#构建模型
prob.solve(solver="GUROBI")#模型求解
print("最优值:", prob.value)
print("最优解:", x.value)
print("钢材剩余量:", right[0] - sum(left[0] * x.value))
print("劳动时间剩余量:", right[1] - sum(left[1] * x.value))
例4
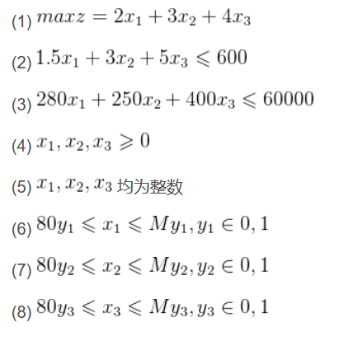
解决这个问题的代码如下
import cvxpy as cp
import numpy as np
coef = np.array([2, 3, 4])
left = np.array([[1.5, 3, 5], [280, 250, 400]])
right = np.array([600, 60000])
x = cp.Variable(3, integer=True)
y = cp.Variable(3, integer=True)
obj = cp.Maximize(coef @ x)
cons = [x >= 0, left @ x <= right,
y >= 0, y <= 1,
x[0] >= 80 * y[0], x[0] <= 1000 * y[0],
x[1] >= 80 * y[1], x[1] <= 1000 * y[1],
x[2] >= 80 * y[2], x[2] <= 1000 * y[2], ]
prob = cp.Problem(obj, cons)
prob.solve(solver="GUROBI")
print("最优值:", prob.value)
print("最优解:", x.value)
print("钢材剩余量:", right[0] - sum(left[0] * x.value))
print("劳动时间剩余量:", right[1] - sum(left[1] * x.value))
例5
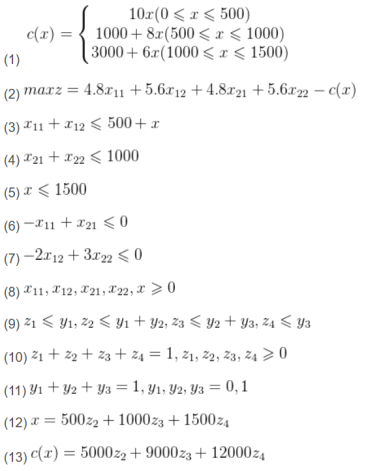
解决这个问题的代码如下
import cvxpy as cp
import numpy as np
coef_x = np.array([4.8, 5.6, 4.8, 5.6])#输入目标函数x对应系数
coef_cx = np.array([0, 5000, 9000, 12000])#输入用z表示cx的系数
coef_buy_x = np.array([0, 500, 1000, 1500])#输入用z表示x的系数
left = np.array([[0, 0, 1, 1], [-1, 0, 1, 0], [0, -2, 0, 3]])#输入约束条件系数
right = np.array([1000, 0, 0])#输入约束条件上限值
x = cp.Variable(4)#创建决策变量x
y = cp.Variable(3, integer=True)#创建0-1变量y
z = cp.Variable(4)#创建变量z
obj = cp.Maximize(coef_x @ x - coef_cx @ z)#构造目标函数
#构造约束条件
cons = [cp.sum(x[0:2]) <= 500 + cp.sum(coef_buy_x @ z),
left @ x <= right,
sum(coef_buy_x @ z) <= 1500,
x >= 0,
z[0] <= y[0], z[1] <= y[0] + y[1], z[2] <= y[1] + y[2], z[3] <= y[2],
cp.sum(z[:]) == 1, z >= 0,
cp.sum(y[:]) == 1,
y >= 0, y <= 1]
prob = cp.Problem(obj, cons)#构造模型
prob.solve(solver="GUROBI")#求解模型
print("最优值:", prob.value)
print("最优解:", x.value)
print("购买原油A:", sum(coef_buy_x * z.value), "t")
例6
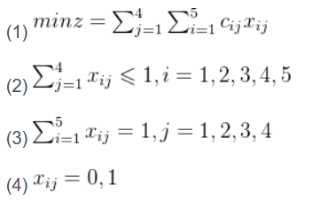
解决这个问题的代码如下
import cvxpy as cp
import numpy as np
#输入目标函数系数
coef = np.array([66.8, 75.6, 87, 58.6,
57.2, 66, 66.4, 53,
78, 67.8, 84.6, 59.4,
70, 74.2, 69.6, 57.2,
67.4, 71, 83.8, 62.4])
x = cp.Variable(20, integer=True)#构造决策变量
#构造目标函数
obj = cp.Minimize(coef @ x)
#输入约束条件
cons = [x >= 0, x <= 1,
cp.sum(x[0:4]) <= 1,
cp.sum(x[4:8]) <= 1,
cp.sum(x[8:12]) <= 1,
cp.sum(x[12:16]) <= 1,
cp.sum(x[16:20]) <= 1,
cp.sum(x[0:20:4]) == 1,
cp.sum(x[1:20:4]) == 1,
cp.sum(x[2:20:4]) == 1,
cp.sum(x[3:20:4]) == 1]
prob = cp.Problem(obj, cons)#构造模型
prob.solve(solver="GUROBI")#模型求解
print("最优值:", prob.value)
print("最优解:", x.value)
例7
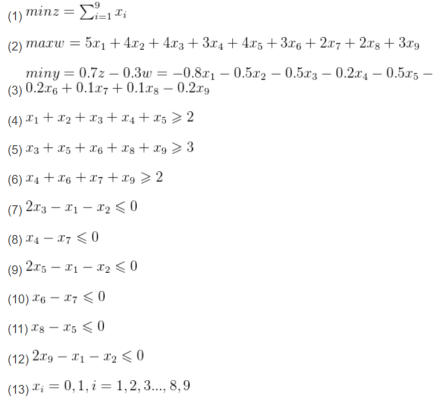
解决这个问题的代码如下
import cvxpy as cp
import numpy as np
#输入目标函数的系数
coef_obj = np.array([-0.8, -0.5, -0.5, -0.2, -0.5, -0.2, 0.1, 0.1, -0.2])
coef_credits = np.array([5, 4, 4, 3, 4, 3, 2, 2, 3])#输入课程学分系数
x = cp.Variable(9, integer=True)#构造决策变量
obj = cp.Minimize(coef_obj @ x)#构造目标函数
#输入约束条件
cons = [cp.sum(x[0:5]) >= 2,
x[2] + [4] + x[5] + x[7] + x[8] >= 3,
x[3] + x[5] + x[6] + x[8] >= 2,
2 * x[2] - x[0] - x[1] <= 0,
x[3] - x[6] <= 0,
2 * x[4] - x[0] - x[1] <= 0,
x[5] - x[6] <= 0,
x[7] - x[4] <= 0,
2 * x[8] - x[0] - x[2] <= 0,
x >= 0, x <= 1]
prob = cp.Problem(obj, cons)#模型构建
prob.solve(solver="GUROBI")#模型求解
print("选课结果:", x.value)
print("学分总和:", sum(coef_credits * x.value))
3.9 动态规划与贪心算法
动态规划和递归问题是算法研究中一项非常经典的话题啦。这一类问题更多的会考虑一个局部最优与全局最优的问题,是离散优化中一项重要的组成部分。
3.9.1 递归与动态规划
我想读者朋友在这里第一次看到“递归”应该是在2.1节当中我提到行列式的求法的时候。当时读者朋友可能就有些疑惑,这个“递归展开”和“递归到最后”应该作何理解?究竟何为递归?我这里呢,可以举个简单的例子:
读者朋友在上小学的时候可能听过这样一个数学故事叫做生兔子:一对小兔子,在成长一年后就可以生下一对小兔子,小兔子再长一年就又能生下一对新的小兔子......这个兔子数列又叫斐波那契 (Fibonacci) 数列,形式是$1,1,2,3,5,8,\dots$。那么,如果不考虑兔子死亡,我怎么推算一百年以后有多少只兔子呢? 我们知道,斐波那契数列的算法是从第三项往后,每一项等于前两项之和。如果我们把它写成数学上的递推公式,它就被写作:
$$ F{n} = F{n-1} + F_{n-2}, n \geqslant 3. \tag{3.9.1}
$$ 而斐波那契数列的前两项为$1$。如果我们把这个公式翻译为python代码,为:
def fibonacci(n):
if n == 1 or n == 2:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
这段代码最有意思的地方就是这个函数好像在“自己调用自己”,这就是递归的结构。如果我想求$F{100}$,我就得先求$F{99}$和$F{98}$,而想求$F{99}$就又得计算$F{98}$和$F{97}$,以此类推一直到$F{2}$和$F{1}$。当我递归到最后的$F{2} = F{1} = 1$时,我就又可以自底而上击破所有的通项。但当读者朋友真的去运行这段代码去求fibonacci(100)的时候会发现python卡在那里久久不能释怀。为什么会造成这么慢的运行速度呢?我们不妨把这个递归结构画出来:
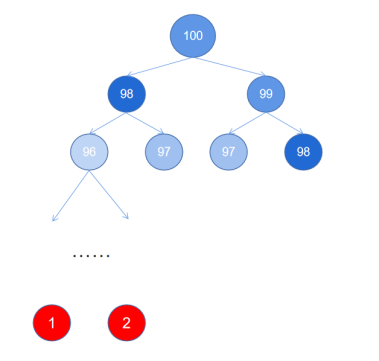
图2.8 为斐波那契数列的递归树示意图。从这个递归树当中可以看到,诸如$F{98}$、$F{97}$等都重复计算了很多次,也正是由于太多次的重复计算导致python算了很多不必要的东西也多了很多不必要的时间开销。能不能尽可能减少重复计算的次数呢?有没有这样的一种办法呢?
一种可行的办法就是把重复计算的东西存到一张表格里面,到时候如果需要计算我可以不用从头开始递归而是采取查表的方法开箱即用。当然,这样子减少重复计算时间开销的代价就是存储这张中间表需要一定的存量,也就是空间开销。这种以空间换时间的方式就是动态规划。而在动态规划当中,最主要的就是上面的递归方程。当然,如果像图这样把问题的递归状态空间树画出来是一种很好的理解方式,但是在画状态空间树的时候其实你会发现搜索过程中对于某些问题有些节点(也就是解)是不合理的,是可以采取剪枝的策略的。这就是一种优化方法。
动态规划没有解题范式,但宏观上有一个通用方法论:
- 问题分解为若干个子问题
- 找状态,选择合适的状态$S(k)$,需要描述多种可能结果的演变
- 做决策,确定决策变量以及可行的动作
- 确定状态转移方程$S(k+1)$=$f(S(k))$
- 确定目标$V(k,n)$,即最终需要达到的目标
- 寻找目标的终止条件
最核心的步骤是找到状态转移方程/递推方程
3.9.2 背包问题的求解
在上一节的最后给的一个背包问题的案例其实就可以用动态规划去做它,由于物品只能是拿与不拿,不能拿一部分,所以又叫0-1背包问题。0-1背包问题在python当中没有内置的函数去调用,所以如果用python写动态规划结构只能自己写因为情况很多很灵活。
以上一节的最后给出的一个背包问题为例,首先我们为了记录方便可以建立一个数组存储每一次操作的背包容量和商品的利润。开始状况下我们的背包容量有$20$,在检索每一个物品的过程中我们会对比物品的体积和包的容量情况,如果体积比现有剩余容量大,我们会考虑需不需要从包中取出某样物品后放入这样物品;如果现有剩余容量还可以装得下它,那么我们也会考虑装下它的最优利润和不装它的最优利润。因为每一次装载会引起容量变化,当容量不再是$20$,物品被排除一样以后最优利润的求解难度也就不一样了;如果子问题能够在我们建立的备忘录数组中检索到,那么这个问题也就可解了。
import numpy as np
m = 5 # 投资总额
n = 6
k = 4 # 项目数
# m元钱,n项投资 k个项目
dp = np.zeros((m, n)) # dp[i][j] 从1-i号项目中选择,投资j万元,所取得的最大收益
mark = np.zeros((m, n)) # 从1-i号项目中选择,投资j万元,获得最大收益时,在第i号项目中投资了多少钱
f = np.array([[0, 0, 0, 0, 0, 0],
[0, 11, 12, 13, 14, 15],
[0, 0, 5, 10, 15, 20],
[0, 2, 10, 30, 32, 40],
[0, 20, 21, 22, 23, 24]])
# 初始化第一行
for j in range(m + 1):
dp[1][j] = f[1][j]
mark[1][j] = j
for i in range(1, k + 1):
for j in range(1, m + 1):
for k in range(j):
if dp[i][j] < f[i][k] + dp[i - 1][j - k]:
dp[i][j] = f[i][k] + dp[i - 1][j - k] # 更新当前最优解
mark[i][j] = k # 更新标记函数
print("最大收益", dp[4][5])
for i in range(1, k + 1):
for j in range(m + 1):
print("(%d, %d)" % (dp[i][j], mark[i][j]), end="\t")
print("\n")
for i in range(k, 0, -1):
print(f"第{i}个项目投资{mark[i][m]}元")
m = m - int(mark[i][m])
3.9.3 贪心策略
如果读者对算法感兴趣,可能还听说过一个概念叫贪心策略。这个东西又是什么呢?还是以上面的背包问题举例子,如果是一个贪心策略的人,它就不会考虑容量问题和全局最优,他只想着怎么把当前的最优选择拿到。他第一步会选择货物1因为它最贵重,这个时候你只剩下了12吨;第二步看到第二贵重的6号货物,这时他只剩下6吨空余;第三步他看到第三贵重的4号货物并装上车,结果只剩下了1吨什么也装不了。但显然,这并不是使利益最大化的方案。
贪心策略在某些问题中往往是有效的,因为它坚信“只要我每一步的选择都是最好的,我最后的结果一定是最好的”。而动态规划是一种全局思想,它认为“我暂时可以不要那么好的选择,退而求其次,但我能保证最后的结果最好”。
二者最大的共同之处就在于:它们的思想都是通过每一步选择一件物品来把原始问题划分为子问题,都有子问题结构和可分性。而且它们的最终目标都是使得最后的总价值是最优的。但究竟什么问题适合贪心,什么问题适合动态规划,尚需要读者见招拆招。
3.10 博弈论与排队论初步
3.10.1博弈论
博弈可分为合作与非合作两种,其核心差异在于决策者间的相互作用是否能导致一项具有约束力的协议。若有,则为合作博弈;若无,则为非合作博弈。 在合作博弈中,关键问题是如何分享合作带来的成果;而在非合作博弈中,每个决策者都需考虑如何选择自身行动,即决策变量的取值。更广泛地说,每个决策者必须制定自身的行动策略,决定在何种情况下采取何种行动。根据决策者行动是否同时进行或按顺序进行,非合作博弈可分为静态与动态。 此外,根据决策者在决策时所掌握的信息量不同,非合作博弈可分为完全信息与不完全信息博弈。博弈的要素包括参与者、决策者、策略空间、决策变量的取值范围、效用函数以及决策的目标函数。
例3.9 点球大战 在点球大战中,我们假设踢球方和守门方都有相同的进球概率,用p表示。因此,守门方的失分概率也是$p$,这形成了一个零和博弈。在这种情况下,踢球方得分的概率也是$p$,与守门方失分概率相等。
| 扑向左边 | 扑向右边 | |
|---|---|---|
| 踢到左边 | 0.58 | 0.95 |
| 踢到右边 | 0.93 | 0.70 |
Nash 均衡:单向改变战略并不能提高自己效用,即每一方的策略对对方而言都是最优的点球大战的进球概率。
$$ \begin{align} S{1} &= \left{ p=(p{1}, p{2}): 0 \leqslant p{i} \leqslant 1, \sum\limits{i=1}^{2} p{i} = 1 \right} \tag{3.10.1}\ S{2} &= \left{ q=(q{}{1}, q{2}): 0 \leqslant q{i} \leqslant 1, \sum\limits{i=1}^{2} q{i} = 1 \right} \tag{3.10.2}\ \end{align}
$$ 对于守门员来说,他希望平均的进球概率尽可能小,但攻球人的目标相反:
$$ \max{p} \min{q} p^{\top}Mq, \tag{3.10.3}
$$ 对函数进行进一步优化:
$$ \begin{align} y &= \max{p} \min{q} p^{\top}Mq\ &= (0.23 - 0.6p)q + (0.25p + 0.7)\ &= (0.25 - 0.6q)p + (0.23q + 0.7)\ \end{align} \tag{3.10.4}
$$
棒球的得分概率也有一个类似于点球大战的目标:

击球手为了使击球平均分最大,面临什么样的约束呢?投球手可以全部投出快球或者弧线球,也就是说,投球手可以采用它的两个纯策略之一来应对击球手的混合策略,这两个纯策略给击球手最大化击球平均分能力施加了一个上限。 此时原问题可以退化为一个线性规划问题:
$$ \begin{align} \text{maximize}~& A \[0.5em] \text{s.t.}~ & A < 0.4p{1} + 0.1(1-p{1})\ & A < 0.2p{1} + 0.3(1-p{1}) \end{align} \tag{3.10.5}
$$ 其中
- $A$:击球平均分
- $p$:击球手猜中快球的比例
- $1-p$:击球手猜中弧线球的比例。
投球手为了使击球平均分最小,面临什么样的约束?击球手可以全部猜测快球或者弧线球。也就是击球手可以采用两个纯策略之一应对投球手的混合策略,这两个纯策略给投球手最小化击球平均分的能力施加了一个下限。
$$ \begin{align} \text{minimize}~& A \[0.5em] \text{s.t.}~ & A > 0.4p{1} + 0.2(1-p{1})\ & A > 0.1p{1} + 0.3(1-p{1}) \end{align} \tag{3.10.6}
$$ 其中
- $q$:投球手投出快球的比例
- $1-q$:投球手投出弧线球的比例
例3.10 企业经营策略博弈
企业的经营活动可以被视作一种博弈,其目标是找到一种策略,无论经济环境如何变化,都能够保障企业获得稳定的经营结果。
 在这个模型中,$V$ 代表企业的净利润,$x$ 表示企业采用小规模生产策略的比例,$(1-x)$ 则代表企业采用大规模生产策略的比例。
当经济环境较为不利时,企业的利润满足 $V<500x+100(1-x)$;而当经济环境较为有利时,企业的利润满足 $V<300x+900(1-x)$。
因此,我们可以将这一问题总结为以下的线性规划优化问题:
在这个模型中,$V$ 代表企业的净利润,$x$ 表示企业采用小规模生产策略的比例,$(1-x)$ 则代表企业采用大规模生产策略的比例。
当经济环境较为不利时,企业的利润满足 $V<500x+100(1-x)$;而当经济环境较为有利时,企业的利润满足 $V<300x+900(1-x)$。
因此,我们可以将这一问题总结为以下的线性规划优化问题:
$$ \begin{align} \text{maximize}~& V \[0.5em] \text{s.t.}~ & V<500x+100(1-x)\ & V<300x+900(1-x)\ & 0<x<1 \end{align} \tag{3.10.7}
$$
通过线性规划方法,我们发现当$x=0.8$时取得了最优解。这意味着企业应该在$80\%$的时间内采用小规模生产策略,在$20\%$的时间内采用大规模生产策略,这是一种相对保守的经营策略。
例3.11 经济的博弈
经济的运行也可以被视为一种博弈,其目标是预测经济可能采取的最不利情形。 在这一模型中,$V$代表企业的净利润,$y$表示经济采用差策略的比例,$(1-y)$则表示经济采用好策略的比例。有$V>500y+300(1-y)$企业采用纯小规模生产的策略; 当经济采用差策略时,企业的利润满足$V>500y+300(1-y)$;而当经济采用好策略时,企业的利润满足 $V>100y+900(1-y)$。 因此,我们可以将这一问题总结为以下的线性规划优化问题:
$$ \begin{align} \text{maximize}~& V \[0.5em] \text{s.t.}~ & V>500y+300(1-y)\ & V>100y+900(1-y)\ & 0<y<1 \end{align} \tag{3.10.8}
$$
通过线性规划方法,我们发现当$y=0.6$时取得了最优解。这意味着经济中60%的策略是不利的,而40%的概率是有利的。
在部分冲突博弈中,参与者的目标是什么?在完全冲突的情形中,每个参与者希望最大化 ta 的支付,在这个过程中同时最小化另一个参与者的支付。但是在部分冲突博弈中,一个参与者可能会有以下目标中的任意一个目标:
- 最大化 ta 的支付: 每个参与者选择一个策略,希望最大化他的支付。当一个参与者推理另一个参与者应该如何应对时,这个参与者不会把保证另一个参与者得到“公平的”结果作为目标,参与者最大化他自己的支付。
- 找到一个稳定的结果: 参与者通常会有兴趣找到一个稳定的结果,纳什均衡结果是任何一个参与者都不能单方面得到进一步改善的结果,因此代表了一种稳定的结果。
- 最小化对手支付: 假设有两家公司,其产品市场相互作用,但不是完全冲突的,每家公司可能从最大化自身支付开始,但如果对结果不满意,这两家公式可能会变成敌对,并选择最小化另一支付的目标,也就是说一个参与者可能会放弃它最大化自己利润的长期目标,并选择最小化对手利润的短期目标。
- 找到一个共同公平的结果,这可能是在仲裁人的帮助下得到的: 两个参与者可能都对当前的状况不满意,相互最小化对方所得到的结果可能对双方都是很差的,在这种情况下,参与者可能会同意接受仲裁者的决策,而仲裁者必须确定一个公平的解。
演化博弈
不同于传统的经典博弈论,演化博弈理论是把博弈理论分析和动态演化过程分析结合起来的一种理论,其强调的是一种动态理论。Maynard Smith和Price将生物进化理论引入到博弈论提出演化博弈论,在演化博弈论中的纳什均衡是参与方根据各自所面对的环境不断调整决策最终实现均衡的动态过程。
在传统博弈理论中,常常假定参与人是完全理性的,且参与人在完全信息条件下进行的,但在现实的经济生活中的参与人来讲,参与人的完全理性与完全信息的条件是很难实现的。在企业的合作竞争中,参与人之间是有差别的,经济环境与博弈问题本身的复杂性所导致的信息不完全和参与人的有限理性问题是显而易见的。
完全理性对博弈主体的理性要求十分严格,因为理性程度高可以使得博弈数学分析更加方便可靠。然而实际生活中的决策环境十分复杂,信息存在着不对称等现象,博弈方很难掌握所有的信息并进行完全理性的思考,因此有限理性才是比较实际的做法。很显然有限理性博弈需要考虑的因素更多,它比完全理性博弈更加复杂,而演化博弈就是一种有限理性的博弈方法,复制动态和演化稳定策略则是演化博弈的核心。
例3.12 中小企业和银行的演化博弈
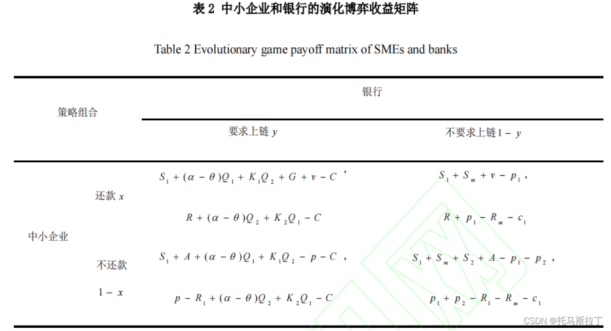
演化博弈的动态方程如下:
$$ \begin{align} F(x) &= x(E{x} - \bar{E}{x}),\ F(y) &= y(E{y} - \bar{E}{y}). \end{align} \tag{3.10.9}
$$
以中小企业为例,复制动态方程为:
$$ \begin{align} F(x) &= \frac{\mathrm{d}x}{\mathrm{d}t}\ &= x(E{x} - \bar{E}{x})\ &= x\Big[E{x} - xE{x} - (1-x)E{1-x}\Big]\ &= x(1-x)(E{x} - E{1-x})\ &= x(1-x)\Big[ y(G - p{2} + S{2}) + x + p{2} - A - S_{2} \Big]. \end{align} \tag{3.10.10}
$$
同理,可以计算得到银行的复制动态方程为:
$$ \begin{align} F(x) &= \frac{\mathrm{d}y}{\mathrm{d}t}\ &= y(E{y} - \bar{E}{y})\ &= y\Big[E{y} - yE{y} - (1-y)E{1-y}\Big]\ &= y(1-y)(E{y} - E{1-y})\ &= y(1-y)\Big[ x(x{2} - p) + p - C + (a - \theta)Q{2} + K{2}Q{1} - p{1} - p{2} + c{1} + R_{m}\Big]. \end{align} \tag{3.10.11}
$$
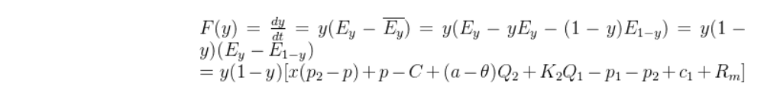 对于中小企业,令$F(x) = 0$,即可得到三个可能的均衡解:
对于中小企业,令$F(x) = 0$,即可得到三个可能的均衡解:
$$ \begin{cases} x{1}^{*} = 0,\ x{2}^{} = 1,\ \displaystyle y^{} = \frac{A+S{2}-v-p{2}}{G + S{2} - p{2}}. \end{cases} \tag{3.10.12}
$$
对于银行,令$F(y)=0$,即可得到三个可能的均衡解:
$$ \begin{cases} y{1}^{*} = 0,\ y{2}^{} = 1,\ \displaystyle x^{} = \frac{C+p{1}+p{2}-p-(a-\theta)Q{2}-K{2}Q{1}-c{1}-R{m}}{p{2}-p}. \end{cases} \tag{3.10.13}
$$
于是,可能的稳定平衡点有$(0,0)$、$(1,1)$、$(0,1)$、$(1,0)$与${(x^,y^)|x^, y^ \in (0,1)}$。
实现这个问题的代码如下:
#各博弈主体动态复制方程
def f(x,y):
return x*(1-x)*(5*y-2.5)
def g(x,y):
return y*(1-y)*(4*x-2)
#initX-x初始值
#initY-y初始值
#dt-步长
#epoch-迭代次数
def calculateValue(initX, initY, dt, epoch):
x = []
y = []
#演化初始赋值
x.append(initX)
y.append(initY)
#微量计算及append
for index in range(epoch):
tempx = x[-1] + (f(x[-1],y[-1])) * dt
tempy = y[-1] + (g(x[-1],y[-1])) * dt
x.append(tempx)
y.append(tempy)
return (x, y)
plt.figure(figsize=(7,7))
D=[]
#随机生成200个初始点
for index in range(200):
random_a=np.random.random()
random_b=np.random.random()
#步长dt为0.001 迭代次数1000
d=calculateValue(random_a,random_b,0.001,1000)
D.append(d)
for n,m in D:
plt.plot(n,m)
plt.ylabel("$y$",fontsize=25)
plt.xlabel("$x$",fontsize=25)
plt.tick_params(labelsize=25)
plt.xticks([0,0.2,0.4,0.6,0.8,1])
plt.grid(linestyle=":",color="b",linewidth=1)
plt.show()
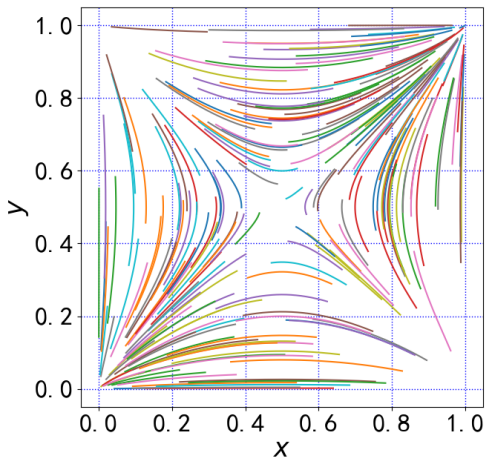
Z = -0.5
D=[]
for index in range(200):
random_a=random.random()
random_b=random.random()
d=calculateValue(random_a,random_b,0.001,1000)
D.append(d)
p1.add_subplot(1,2,1)
for n,m in D:
plt.plot(n,m)
plt.title("Z=-0.5",fontsize=25)
plt.ylabel("$y$",fontsize=25)
plt.xlabel("$x$",fontsize=25)
plt.tick_params(labelsize=25)
plt.xticks([0,0.2,0.4,0.6,0.8,1])
# plt.title("Phase space")
plt.grid(linestyle=":",color="b",linewidth=1)
Z = 1
D=[]
for index in range(200):
random_a=random.random()
random_b=random.random()
d=calculateValue(random_a,random_b,0.001,1000)
D.append(d)
p1.add_subplot(1,2,2)
for n,m in D:
plt.plot(n,m)
plt.title("Z=1",fontsize=25)
plt.ylabel("$y$",fontsize=25)
plt.xlabel("$x$",fontsize=25)
plt.tick_params(labelsize=25)
plt.xticks([0,0.2,0.4,0.6,0.8,1])
# plt.title("Phase space")
plt.grid(linestyle=":",color="b",linewidth=1)
plt.show()
例3.13参考https://blog.csdn.net/qq_25990967/article/details/122929001,特别鸣谢!
例3.13 以电动出租车与换电站为例,假设电动出租车及换电站均属于同一家公司,公司想通过换电站价格定价措施去控制目标区域内的出租车数量达到预期分布。
对于司机而言,有两个成本,一个是距离成本$d$,一个是支付成本$p$,支付成本即是换电地所支付的电价,我们可以设立权重因子$a$将两者合并构建为一个效用函数,司机会选择该函数最小的换电站更换电池,更换电池后可机一般会在周围开始接单:
$$U_n =a_1\cdot d_n^i +a_2\cdot p_i, \tag{3.10.14}$$ 对于公司而言,目标函数则是不同地区的出租车实际分布e与期望分布E的绝对差之和,公司通过调整价格去影响司机的选择,从而调整司机在不同区域的分布:
$$ \min{\boldsymbol{p}} \sum\limits{i=1}^{m} |e{i} - E{i}|. \tag{3.10.15}
$$
出租车与换电站的安排:
- 第一阶段,充电站统计出各电动出租车的换电请求后,根据优化目标,制定价格策略
- 第二阶段,电动出租车根据自身效用函数从所有换电站中选择出目标换电站进行跟换电池
- 第一阶段和第二阶段交替往复进行,直到达到均衡
代码实现如下:
#导入相关库
import numpy as np
import math
import random
from collections import Counter
import matplotlib.pyplot as plt
#解决图标题中文乱码问题
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
#初始化各参数
n=900 #换电需求数
min_price=170 #换电价格范围
max_price=230
A=np.random.normal(36, 5, 25) #初始期望,平均值为36,方差为5的高斯分布
E=np.floor(A)#朝0方向取整,如,4.1,4.5,4.8取整都是4
# 下面是根据需求数调整E的大小
E=np.floor(A)
a=sum(E)-n
A=A-a/25
E=np.floor(A)
b=sum(E)-n
A=A-b/25
E=np.floor(A)
a1=0.05;a2=0.95;#距离成本与换点价格权重
x=[random.random()*20000 for i in range(n)]#初始化需求车辆位置
y=[random.random()*20000 for i in range(n)]
H=np.mat([[2,2],[2,6],[2,10],[2,14],[2,18],
[6,2],[6,6],[6,10],[6,14],[6,18],
[10,2],[10,6],[10,10],[10,14],[10,18],
[14,2],[14,6],[14,10],[14,14],[14,18],
[18,2],[18,6],[18,10],[18,14],[18,18]])*1000
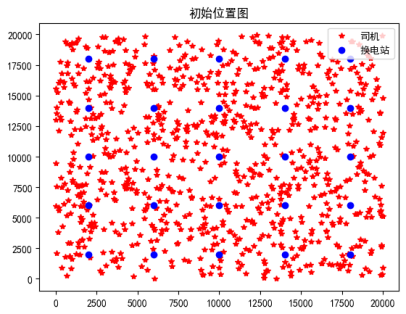
# 制初始化的司机与换电站的位置图
plt.plot(x,y,'r*')
plt.plot(H[:,0],H[:,1],'bo')
plt.legend(['司机','换电站'], loc='upper right', scatterpoints=1)
plt.title('初始位置图')
plt.show()
# 计算期望与实际期望
D=np.zeros((len(H),n)) #需求车辆到各换电站的需求比例
price=200*np.ones((1,25))
for i in range(len(H)):
for j in range(len(x)):
D[i,j]=a1*np.sqrt(((H[i,0]-x[j]))**2+(H[i,1]-y[j])**2)+a2*price[0,i]
D=D.T #转置
D=D.tolist() #转为列表格式
d2=[D[i].index(np.min(D[i])) for i in range(n)]
C = Counter(d2)
e=list(C.values())
err=sum(abs(E-e)) #期望差之和,即博弈对象
#博弈过程
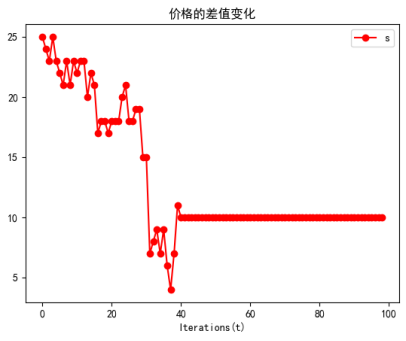
J=[] #价格变化的差值
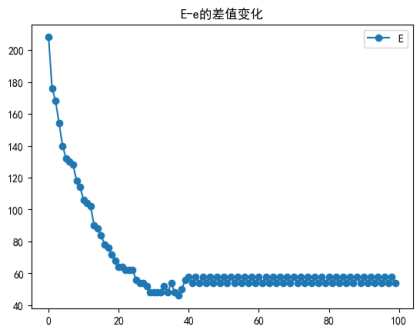
ER=[err] #E-e的变化差值
for k in range(1,100):
j=0
for i in range(25):
if e[i] < E[i] and price[0,i] >= min_price:
price[0,i] = price[0,i]-1
j=j+1
if e[i] > E[i] and price[0,i] <= max_price:
price[0,i] = price[0,i]+1
j=j+1
J.append(j)
DD=np.zeros((len(H),n)) #需求车辆到各换电站的需求比例
# price=200*np.ones((1,25))
for i in range(len(H)):
for j in range(len(x)):
DD[i,j]=a1*np.sqrt(((H[i,0]-x[j]))**2+(H[i,1]-y[j])**2)+a2*price[0,i]
DD=DD.T #转置
DD=DD.tolist() #转为列表格式
dd2=[DD[i].index(np.min(DD[i])) for i in range(n)]
C = Counter(dd2)
e=[C[i] for i in sorted(C.keys())]
err=sum(abs(E-e)) #期望差之和,即博弈对象
ER.append(err)
#绘制图
plt.plot(ER,'-o')
plt.title('E-e的差值变化')
# plt.set(gcf,'unit','normalized','position',[0.2,0.2,0.64,0.32])
plt.legend('E-e')
# plt.grid(ls=":",c='b',)#打开坐标网格
plt.show()
plt.plot(J,'r-o')
plt.title('价格的差值变化')
plt.xlabel('Iterations(t)')
plt.legend('sum of Price(t)-Price(t-1)')
# plt.grid(ls=":",c='b',)#打开坐标网格
plt.show()
plt.bar(x = range(1,26), # 指定条形图x轴的刻度值
height=price[0],
color = 'steelblue',
width = 0.8
)
plt.plot([1,26],[min_price,min_price],'g--')
plt.plot([1,26],[max_price,max_price],'r--')
plt.title('换电站的换电价格')
plt.ylabel('Price(¥)')
plt.axis([0,26,0,300])
# plt.grid(ls=":",c='b',)#打开坐标网格
plt.show
index = np.arange(1,26)
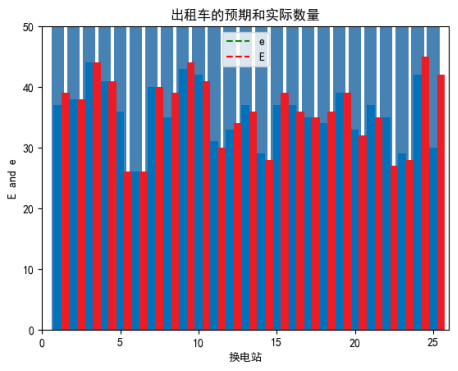
rects1 = plt.bar(index, e, 0.5, color='#0072BC')
rects2 = plt.bar(index + 0.5, E, 0.5, color='#ED1C24')
plt.axis([0,26,0,50])
plt.title('出租车的预期和实际数量')
plt.ylabel('E and e')
# plt.grid(ls=":",c='b',)#打开坐标网格
plt.xlabel('换电站')
plt.legend(['e','E'])
plt.show()
3.10.2 排队论
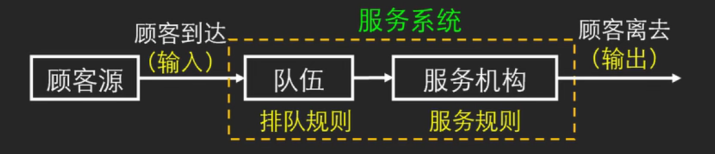
排队论,又称随机服务系统理论,是应用数学的一个分支,专门研究和解决拥挤现象问题。其研究内容主要涵盖以下三个方面:
- 性态问题:主要研究各种排队系统的概率规律性,包括队列长度分布、顾客等待时间分布以及系统忙期分布等。性态问题包括瞬态和稳态两种情形。
- 最优化问题:包括静态最优和动态最优。静态最优指的是最佳系统设计,即如何设计排队系统以最大化效率或最小化成本。而动态最优则涉及最佳运营策略,即在实际运行中如何调整服务机制以优化系统性能。
- 统计推断问题:主要用于判断排队系统的类型,以便进行进一步分析和优化。
在排队系统中,顾客从顾客源(总体)出发,到达服务机构(服务台、服务员)前排队等候接受服务,服务完成后再离开。排队结构指的是队列的数量和排列方式,而排队规则和服务规则则说明了顾客按照何种规则和次序接受服务。
一个排队系统包括:
- 在一定时间内顾客平均到达多少?
- 按什么规律到达(输入过程服从什么分布)?
- 进入系统的顾客按照什么规则排队?
- 服务机构设置多少服务设施?排列形式?
- 服务时间服从什么分布?
表1:表示相继到达间隔时间和服务时间的各种分布的符号 符号 含义
输入 顾客到达分布
输出 服务时间分布 M (Markov) 负指数分布 Negative Exponential D 确定型Deterministic GI 一般相互独立分布 General Independent Ek K阶爱尔朗分布 Erlang distribution G 一般服务时间分布 General 服务规则 FCFS 先到先服务 LCFS 后到先服务 PR 带优先权服务 SIRO 随机服务
排队系统的要素:
- $X$: 相继到达的间隔时间的分布,一般为负指数分布
- $Y$: 服务时间的分布,一般为负指数分布或者确定性
- $Z$: 服务台的数目,1台或者多台
- $A$: 系统客量的限制,系统中是否存在顾客的最大数量限制
- $B$: 顾客源数目,顾客源是否有限
- $C$: 服务规则,先到先服务或者后到先服务等
| 数量指标 | 符号 | 含义 |
|---|---|---|
| 队长 | $L_s$ | 系统中的平均顾客数 |
| 等待队长的数量 | $L_q$ | 系统中处于等待的顾客的数量 |
| 平均逗留时间 | $W$ | 顾客进入系统到离开系统的这段时间 |
| 平均等待时间 | $W_a$ | 顾客进入系统到接受服务的这段时间 |
| 平均到达率 | $\lambda$ | 单位时间内平均到达的顾客数 |
| 平均服务率 | $\mu$ | 单位时间内受到服务的顾客平均数 |
| 单个服务台的服务强度 | $p$ | 每个服务台在单位时间内的服务强度 |
| 平均负荷 | $\rho$ | 单个服务台在单位时间内的平均负荷 |
智能仓库中配置多个搬运机器人,中心控制系统接收到订单后,经过分析拆解为相应的拣选任务,然后根据任务优先级,通过一定的分配算法,将任务分配给当前处于空闲状态的搬运机器人。这里,我们将订单看作顾客,搬运机器人看作服务台,不考虑系统对订单的处理及任务分配过程。那么,整个系统可以抽象为一个多服务台排队系统(M/M/C)。
对于仓库机器人数量分析问题,若只考虑订单到达和机器人搬运的过程,那么可以将该问题简化为排队论中的多服务台排队系统(M/M/N),前两个M表示顾客到达时间间隔和机器人服务时间均服从负值数分布,C表示为多个服务台,所以M/M/1即表示单服务台系统。基本的思路是:将拣选机器人看作服务台,因为仓库中是由多个搬运机器人组成的多机器人系统,所以是多个服务台;此外,假设顾客(即订单)到达时间间隔和机器人服务时间都服从负值数分布。通过以上简化,即可将仓库机器人数量需求分析问题简化为M/M/C问题。
排队论中有几个重要的指标:系统服务强度$\rho$,系统空闲概率$p_{0}$,系统平均排队等待的订单数$L_q$,系统中平均订单数(包括排队等待和正在接受服务的订单)$L_s$,系统中订单的平均等待时间$W_q$,系统中订单的平均逗留时间(包括等待时间和接受服务时间)$W_s$,上面几个指标的计算公式如下:
$$ \begin{align} \rho &= \frac{\lambda}{C\mu}, \tag{3.10.16}\ p{0} &= \left[ \sum\limits{k=1}^{C-1} \frac{1}{k!}\left( \frac{\lambda}{\mu} \right) + \frac{1}{C!(1-\rho)}\left( \frac{\lambda}{\mu} \right)^{C} \right]^{-1}, \tag{3.10.17}\ L{q} &= \frac{(C\rho)^{C}\rho}{C!(1-\rho)^{2}}\cdot p{0}, \tag{3.10.18}\ L{s} &= L{q} + \frac{\lambda}{\mu}, \tag{3.10.19}\ W{q} &= \frac{L{q}}{\lambda}, \tag{3.10.20}\ W{s} &= \frac{L{s}}{\lambda}. \tag{3.10.21} \end{align}
$$
输入$300$,$12$,$20$,即达到率为$300$个/小时,服务率为$12$个/小时,机器人数量为$30$,执行代码后可得到结果:
def factorials(x):
'''
利用递归的阶乘计算函数
:return:
'''
if x == 0 or x == 1:
return 1
else:
return x * factorials(x - 1)
class QueuingTheory(object):
def __init__(self, ar, sr, snum):
'''
排队论模型初始化
:param ar:顾客到达率
:param sr:机构服务率
:param snum:服务台数量
'''
self.ar = ar
self.sr = sr
self.snum = snum
self.ro = self.ar / self.sr
self.ros = self.ar / (self.sr * self.snum)
self.p0 = self.P0_Compute() #系统中所有机器人空闲的概率
self.cw = self.CW_Compute() #系统中订单排队的概率
self.lq = self.Lq_Compute() #系统中排队等待的平均订单数
self.ls = self.lq + self.ro #系统中的平均订单数
self.rw = (self.snum - self.ls) / self.snum #系统中单个机器人的平均空闲率
self.ws = self.ls / self.ar #系统中订单的平均等待时间
self.wq = self.lq / self.ar #系统中订单的平均排队时间
def P0_Compute(self):
'''
系统中所有机器人空闲的概率
:return:
'''
result = 0
ro, ros = self.ar / self.sr, self.ar / (self.sr * self.snum)
for k in range(self.snum):
result += ro ** k / factorials(k)
result += ro ** self.snum / factorials(self.snum) / (1 - ros)
return 1/result if (1/result)>0 else 0
def CW_Compute(self):
'''
订单排队的概率
:return:
'''
ro, ros = self.ar / self.sr, self.ar / (self.sr * self.snum)
return ro ** self.snum * self.p0 / factorials(self.snum) / (1 - ros)
def Lq_Compute(self):
'''
排队等待的平均订单数
:return:
'''
ros = self.ar / (self.sr * self.snum)
return self.cw * ros / (1- ros)
def main():
ar, sr, snum = list(map(float, input('请输入系统到达率,服务率和服务台数量').split(',')))
snum = int(snum)
myqueuing = QueuingTheory(ar, sr, snum)
print('系统中所有机器人空闲的概率为%6.3f'% myqueuing.p0)
print('系统中订单排队的概率为%6.3f' % myqueuing.cw)
print('系统中单个机器人的平均空闲率为%6.3f' % myqueuing.rw)
print('系统中排队等待的平均订单数为%6.3f' % myqueuing.lq)
print('系统中的平均订单数为%6.3f' % myqueuing.ls)
print('系统中订单的平均排队时间为%6.3f分钟' % (myqueuing.wq * 60))
print('系统中订单的平均等待时间为%6.3f分钟' % (myqueuing.ws * 60))
print('系统总成本为%6.3f元' % (1000*snum + myqueuing.lq*100))
if __name__ == '__main__':
main()
结果表明系统中平均同时存在 25 个订单,包括正在接受服务的和排队等待服务的订单。每个订单平均等待 5 分钟才能开始接受服务。最终系统的总成本为20000元。
3.11 多目标规划
一直到2.5节为止我们已经见到了各种各样的规划,当读者将这些内容全部读完并能有针对性地进行思考和扩展时,你已经具备了能够解一定难度规划题的能力。多目标规划实际上也并不难理解,就是说目标函数可能不止一个。譬如,当你进行投资选股的时候,并不会简单地考虑收益最大,还会考虑风险。在市场上,no risk, no gain,但这个风险你并不一定承担得起,所以你会综合考虑多个优化目标。有关投资选股的策略我们在后续章节中也会简单介绍一些策略,但现在我们的目的是考虑如何解决多目标规划。
从非线性规划的标准形式出发,我们定义一个二目标规划(其实多目标的策略和二目标也是一样的):
$$ \begin{align} \text{minimize}~& f(x), g(x) \[0.5em] \text{s.t.}~ & Ax \leqslant b\ & C(x) \leqslant 0\ & A{\text{eq}}x = b{\text{eq}}\ & C{\text{eq}}(x) = 0\ & l{b} \leqslant x \leqslant u_{b} \end{align} \tag{3.11.1}
$$ 多目标规划最常见的思路就是去将多目标问题转化为单目标问题求解,那么就需要对二目标进行综合。要想把它们综合起来也很容易,我可以根据经验或者资料取一个合适的常数对其进行加权求和,像这样:
$$ \begin{align} \text{minimize}~& f(x) + \lambda g(x) \[0.5em] \text{s.t.}~ & Ax \leqslant b\ & C(x) \leqslant 0\ & A{\text{eq}}x = b{\text{eq}}\ & C{\text{eq}}(x) = 0\ & l{b} \leqslant x \leqslant u_{b} \end{align} \tag{3.11.2}
$$
通过这种手段把它变成一个单目标规划就好解决了。而常数的取值我们也可以测试不同的数值,在后续也可以探讨最优解与这个常数取值之间的关系(它往往被视作一种灵敏性分析)。
另一种常见的手段是取乘积或者取比值。比如如果我们想最小化风险R并最大化收益E,我们可以最大化这样一个目标函数:
$$\text{maximize}~ \frac{E(x)}{R(x)}, \tag{3.11.3}$$ 后续章节也会看到这两种综合策略在投资选股问题中的不同。
另一种常见的方法叫理想点法,它基于这样一个事实:与最优解越近的点,其目标函数值往往也越接近最优值。所以在可行域内可以分别求两个目标的最优解,然后再在可行域内找点,让这个点到两个目标最优解的距离之和最小。可以看下面这个例子:
例3.14 某公司考虑试生产两种太阳能电池甲和乙。但生产这两种产品会引起空气污染,因此,有两个目标:极大化利润和极小化总的污染,已经每单位产品收益、污染排放量、机器能力(小时)装配能力(人时)和可用的原材料(单位)的限制如下表所示。假设市场需求无限制,两种产品的产量和至少为10,则该公司应如何安排一个生产周期的生产?
单位甲产品 单位乙产品 资源限量
设备工时 0.5 0.25 8
工人工时 0.2 0.2 4
原材料 1 5 72
利润 2 3
污染排放 1 2
在这个场景中,我们有两个目标:极大化利润和极小化污染。我们需要在给定的资源限制下,确定两种太阳能电池甲和乙的产量,使得这两个目标得到满足。
设甲产品的产量为 xA 单位,设乙产品的产量为xB单位。 目标函数:
- 极大化总利润:maxP = 2xA + 3xB)
- 极小化总污染:min E = xA + xB)
约束条件:
- 机器能力限制:0.5xA+ 0.2xB≤ 8
- 工人工时限制:0.2xA + 4xxB ≤ 4
- 原材料限制: xA + 5xB≤72
- 产量限制: xA,xB≥ 10
import numpy as np
import cvxpy as cp
c1 = np.array([-2, -3])
c2 = np.array([1, 2])
a = np.array([[0.5, 0.25], [0.2, 0.2], [1, 5], [-1, -1]])
b = np.array([8, 4, 72, -10])
x = cp.Variable(2, pos=True)
# 1.线性加权法求解
obj = cp.Minimize(0.5*(c1+c2)@x)
con = [a@x <= b]
prob = cp.Problem(obj, con)
prob.solve(solver='GUROBI')
print('\n======1.线性加权法======\n')
print('解法一理想解:', x.value)
print('利润:', -c1@x.value)
print('污染排放:', c2@x.value)
# 2.理想点法求解
obj1 = cp.Minimize(c1@x)
prob1 = cp.Problem(obj1, con)
prob1.solve(solver='GUROBI')
v1 = prob1.value # 第一个目标函数的最优值
obj2 = cp.Minimize(c2@x)
prob2 = cp.Problem(obj2, con)
prob2.solve(solver='GUROBI')
v2 = prob2.value # 第二个目标函数的最优值
print('\n======2.理想点法======\n')
print('两个目标函数的最优值分别为:', v1, v2)
obj3 = cp.Minimize((c1@x-v1)**2+(c2@x-v2)**2)
prob3 = cp.Problem(obj3, con)
prob3.solve(solver='GUROBI') # GLPK_MI 解不了二次规划,只能用CVXOPT求解器
print('解法二的理想解:', x.value)
print('利润:', -c1@x.value)
print('污染排放:', c2@x.value)
# 3.序贯法求解
con.append(c1@x == v1)
prob4 = cp.Problem(obj2, con)
prob4.solve(solver='GUROBI')
x_3 = x.value # 提出最优解的值
print('\n======3.序贯法======\n')
print('解法三的理想解:', x_3)
print('利润:', -c1@x_3)
print('污染排放:', c2@x_3)
例3.15 求解多目标规划:
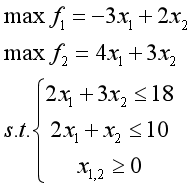
理想点法:
from scipy.optimize import linprog
import numpy as np
c = [-3, 4] # 注意:c的顺序应与变量x的顺序对应,即c[0]对应x[0],c[1]对应x[1]
A = np.array([[2, 3], [2, 1]])
b = np.array([18, 10])
x_0_bounds = (0, None) # x_0的界限是[0, +∞)
x_1_bounds = (0, None) # x_1的界限是[0, +∞)
res = linprog(c, A_ub=A, b_ub=b, bounds=[x_0_bounds, x_1_bounds], method='highs')
if res.success:
print("找到最优解:")
print("x_0 =", res.x[0])
print("x_1 =", res.x[1])
print("目标函数值:", -res.fun)
else:
print("优化未成功:", res.message)
多目标规划还有序贯法等一系列方法可以求解,但求解得到的结果却未必是我们最想要的。因为在多目标规划的时候,目标之间不同的人有不同的权衡。比如投资当中,有人更希望收益更大,宁可冒一点风险;但有一些人小心驶得万年船,更看重风险。莎士比亚说,一千个读者就有一千个哈姆雷特,如何对目标做综合其实是一件富有主观性的工作。所以在多目标规划的问题上,我个人其实更倾向于用加权法做综合来解这类问题。
3.12 Monte Carlo模拟
Monte Carlo方法则是另一种求解规划时常用的方法。它基于一个事实:大量的重复试验下频率可以估计概率,也就是用大规模的候选解模拟出一个近似值逐步逼近精确解。理论上只要实验次数够多精度够细它可以无限逼近精确解。
我想各位上中学的时候还没忘记蒲丰投针估计圆周率的故事吧,如果不幸忘记了,也还记得撒黄豆估计圆周率的方法吧。在一个正方形中画一个内切圆,往正方形内撒一大把黄豆,通过数出圆里面的黄豆和正方形里面的黄豆之比可以估计圆周率的近似值。这一原理也被广泛用于求函数的定积分。图2.3是一个利用Monte Carlo方法求定积分的例子,通过统计方形中点的个数和曲线下方点的个数之比,就可以近似模拟定积分与方形面积之比。
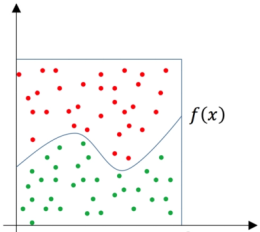
图2.3 利用Monte Carlo方法求定积分的例子
Monte Carlo方法求线性规划的近似最优解我们可以看一个例子:
例3.16 求解下面的线性规划:
将Monte Carlo方法和这个规划都做成函数可以写成如下形式:
from numpy import random as rd
N = 1000000
x_2 = rd.uniform(10, 20.1, N)
x_1 = x_2 + 10
x_3 = rd.uniform(-5, 16, N)
f = float('-inf')
for i in range(N):
if -x_1[i]+2*x_2[i]+2*x_3[i]>=0 and x_1[i]+2*x_2[i]+2*x_3[i]<=72:
result = x_1[i] * x_2[i] * x_3[i]
if result>f:
f = result
final_X = [x_1[i], x_2[i], x_3[i]]
print("""最终得出的最大目标函数值为:%.4f
最终自变量取值为:
x_1 = %.4f
x_2 = %.4f
x_3 = %.4f""" % (f, final_X[0], final_X[1], final_X[2]))