Part 02 Function and Sequence

Covering 2.3~2.4

Functions 函数

Definitions 定义

Let A and B be nonempty sets. A function f from A to B is an assignment of exactly one element of B to each element of A.

We write f (a) = b if b is the unique element of B assigned by the function f to the element a of A.

If f is a function from A to B, we write f : A → B.

A → B is a subset of A × B

Functions are sometimes also called mappings（映射） or transformations（变换）

$f:A\to B$

$\forall a(a\in A\to\exists!b(b\in B\wedge f(a)=b))$

• A : domain（定义域）

• B : codomain（陪域）

• b : image（像）

• a : preimage（原像）

The range（值域）, or image, of f is the set of all images of elements of A.

If f is a function from A to B, we say that f maps（映射） A to B.

Two Notations:

$(f_1+f_2)(x)=f_1(x)+f_2(x)$

$(f_1f_2)(x)=f_1(x)f_2(x)$

Let f be a function from A to B and let S be a subset of A. The image of S under the function f is the subset of B that consists of the images of the elements of S. We denote the image of S by f (S), so

$f(S)={f(s)|s\in S}$

$f(S\cup T)=f(S)\cup f(T)$

$f(S\cap T)\subseteq f(S)\cap f(T)$

Explaination:

For the first equivalent, just prove $f(S+T)\subseteq f(S)+f(T)$ and $f(S)+f(T)\subseteq f(S+T)$ using the method proof by cases

For the second one, itself is easy to prove, but the interesting part is how to give a counterexample to prove that $f(S)\cap f(T)\subseteq f(S\cap T)$ is wrong.

This counterexample is that when f() is not one-to-one (this will be mentioned right below), the latter one can be larger than the previous one! (Specific example omitted)

The graph（图） of the function f is the set of ordered pairs

${(a,b)|a∈A\wedge f(a)=b}$

A monotonic（单调） function f is either monotonically (strictly) increasing ($\forall x\forall y(xf(y))$))

Correspondences 对应关系

One-to-One Function 一对一函数

A function f is one-to-one（一对一） (denoted 1-1), or injective（单射函数）if

$\forall a\forall b(f(a)=f(b)\to a=b)$

Onto Functions 映上函数

A function f from A to B is called onto（映上）, or surjective（满射） if

$\forall b\in B\exists a\in A(f(a)=b)$

In short, every b in B has a preimage.

One-to-one Correspondence Functions 一一对应函数

The function f is a one-to-one correspondence（一一对应）, or a bijection（双射）, if it is both one-to-one and onto

Whenever there is a bijection from A to B, the two sets must have the same number of elements or the same cardinality.

Examples of Different Types of Correspondences

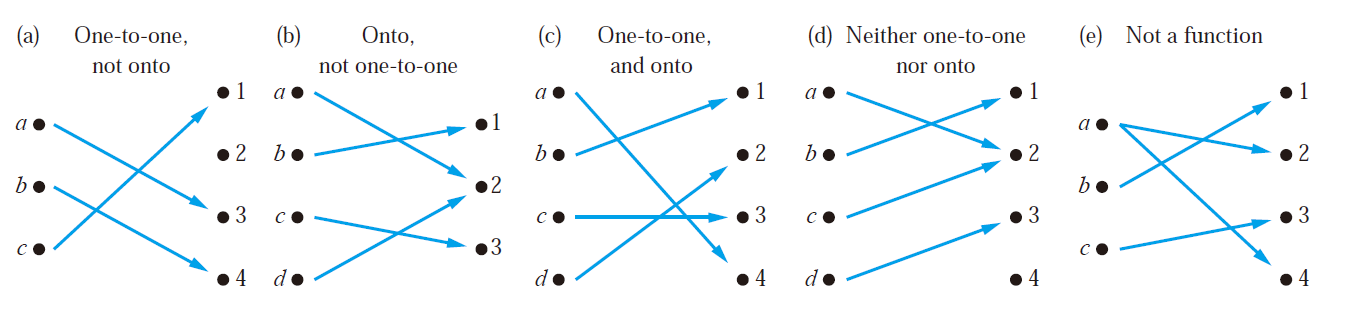
Suppose that f : A → B

• To show that f is injective, show that if f (x) = f (y) for arbitrary x, y ∈ A, x = y.
• To show that f is not injective, find particular elements x, y ∈ A such that x ≠ y and f (x) = f (y).
• To show that f is surjective, consider an arbitrary element y ∈ B and find an element x ∈ A such that f (x) = y.
• To show that f is not surjective Find a particular y ∈ B such that f (x) ≠ y for all x ∈ A.

Special Functions 特殊函数

Inverse Functions 反函数

Let f be a one-to-one correspondence from the set A to the set B, the inverse function of f is denoted by $f^{-1}$

$f^{-1}(y)=x$ iff $f(x)=y$

No inverse function exists unless f is a bijection

Function f is invertible（可逆的） iff f is bijective

Compositions of Functions 复合函数

$f\circ g(a)=f(g(a))$

$f\circ g$ can’t be defined unless the range of g is a subset of the domain of f.

Two Important Functions 两大重要函数

The floor function 取底函数

The floor function f (x) is the largest integer less than or equal to the real number x

$\lfloor x\rfloor$

The floor function is often also called the greatest integer function. It is often denoted by [x]

The ceiling function 取顶函数

$\lceil x\rceil$

Sequence 序列

A sequence is a function from a subset of the set of intergers (usually either the set {0,1,2,…} or the set {1,2,3,…}) to a set S. We use the notation $a_n$ to denote the image of the image of the integer n. We call $a_n$ a term of the sequence ${a_n}$.

The order in a sequence matters!

Some Sequences 一些序列

Geometric Progression 几何级数

$a,ar,ar^2,ar^3,...,ar^n,...$

Arithmetic Progression 算术级数

$a,a+d,a+2d,...,a+nd,...$

Recurrence 递推

e.g. Fibonacci Sequence

Summations 求和

$$ \begin{equation} \sum{i=m}^na_i=\sum\nolimits{i=m}^nai=\sum\nolimits{m≤i≤n}ai=a_m+a{m+1}+...+a_n \end{equation}

$$

$ \sum_{s∈S}f(s) $

Some Useful Summation Formulae 求和公式

$ \sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}{6} $

$ \sum_{k=1}^nk^3=\frac{n^2(n+1)^2}{4} $

$ \sum_{k=1}^{\infin}kx^{k-1}=\frac{1}{(1-x)^2},|x|<1 $