第5章 进化计算与群体智能
内容:@若冰(马世拓)
审稿:@刘旭
排版&校对:@何瑞杰
这一章我们主要介绍进化计算和群体智能算法中四个最常用的算法。传统的优化算法例如我们在第二章看到的分支定界、蒙特卡洛等方法比较适合于简单的、约束和变量不是那么多的优化。但当优化的变量非常之多,约束非常之多,目标函数形式非常之复杂时我们往往 是求不出最优解的。这时候我们通常使用智能优化算法去求近似解。这些算法由于很多从自然中生物行为规律受到启发故又名“仿生计算”。本章主要涉及到的知识点有:
- 遗传算法
- 蚁群算法
- 粒子群算法
- 模拟退火算法
5.1 遗传算法理论与实现
人类总是能够从自然界获取很多灵感。通过蝙蝠的回声定位,我们发明了雷达;通过鱼的游动,我们发明了潜艇;通过鲨鱼的皮肤,我们发明了潜水服……而遗传算法同样是基于生物原理得到灵感。这个灵感,来自于孟德尔遗传定律和达尔文自然选择学说。
5.1.1 遗传算法
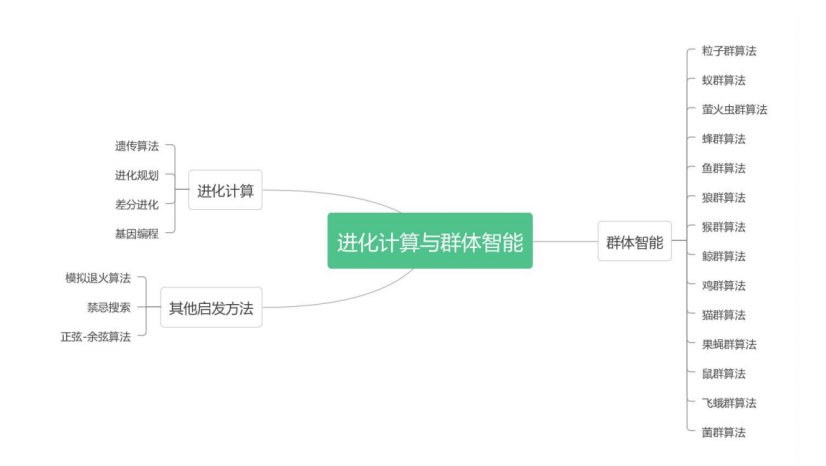
这一章的标题是进化计算与群体智能算法,如果你在其他的资料上看到了“智能优化算法”或者“元启发优化算法”,其实它们说的是一类东西。只是我为什么称之为进化计算与群体智能呢?因为它包含的算法种类真的非常之多,多到令人无法想象。当你看到它们的名字,你会感叹原来自然界为我们提供了如此之多的灵感,诸如蚁群算法,人工鱼群算法,萤火虫群算法,蜂群算法,狼群算法,哈里斯鹰算法……
我将一些常见的智能优化算法按照如图 9.1 所示的方式进行归类汇总。值得注意的是,本章讲解的四个算法是最常用的算法,其它的一些算法虽然灵感上很创新,看起来很炫但实质效果却并没有得到太大的改善。或许运算速度有可能快一些,但从整体来看并没有比本章的这四个算法好多少。
遗传算法是 J.H.Holland 在 1975 年提出,模拟达尔文的遗传选择和自然淘汰的进化过程。这一算法被誉为智能优化算法“根源中的根源”。它被广泛应用于大规模的优化问题,例如非线性规划,离散优化,TSP 问题,VRP 问题,车间调度问题等。
孟德尔在他的遗传学说当中揭示了遗传过程中染色体的一些变化过程:复制,交叉,突变等。而微观的遗传物质的变化影响到了种群在自然界的发展,因为生物的发展与进化主要的过程就是三个:遗传,变异和选择。只有适应环境的竞争力强的生物才能存活下来,不适应者就会消亡。而遗传算法就是借鉴了这一点,通过遗传和变异生成一批候选解,然后在逐代进化的过程中一步步逼近最优解。这里补充几个概念定义:
- 染色体:遗传物质的主要载体,是多个遗传因子的集合。
- 基因:遗传操作的最小单元,以一定排列方式构成染色体。
- 个体:染色体带有特征的实体。
- 种群:多个个体组成群体,进化之初的原始群体被称为初始种群。
- 适应度:用于评价个体适应环境程度的函数值。
- 编码:二进制或十进制去表示研究问题的过程。
- 解码:将二进制或十进制还原为原始问题的过程。
- 选择:以一定概率从种群中选择若干个体的过程,选择的基准方法有很多,常见的有适应度比例法、期望值法、轮盘赌法等。
- 交叉:将两个染色体换组的操作,又称重组。
- 变异:遗传因子按一定概率变化的操作。
遗传算法借鉴了生物学的概念,首先需要对问题进行编码,通常是将函数编码为二进制代码以后,随机产生初始种群作为初始解。随后是遗传算法的核心操作之一——选择,通常选择首先要计算出个体的适应度,根据适应度不同来采取不同选择方法进行选择,常用方法有适应度比例法、期望值法、排位次法、轮盘赌法等。
在自然界中,基因的突变与染色体的交叉组合是常见现象,这里也需要在选择以后按照一定的概率发生突变和组合。不断重复上述操作直到收敛,得到的解即最优。遗传算法基本思想如图 9.2 所示:
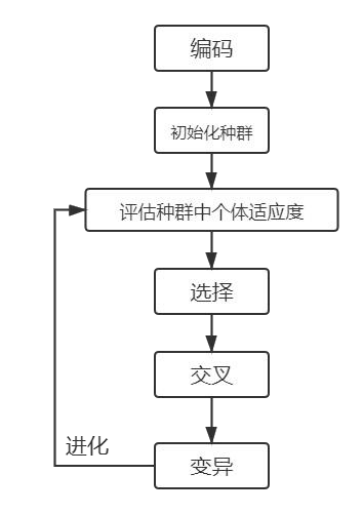
注意:其实遗传算法说起来这么复杂,实际上思想本质上还是一个搜索。从一堆可行解里面搜索最优解,没有方向漫无目的的检索叫暴力搜索,有方向的才叫启发式搜索。遗传算法的方向就是进化。
5.1.2 遗传算法的实现
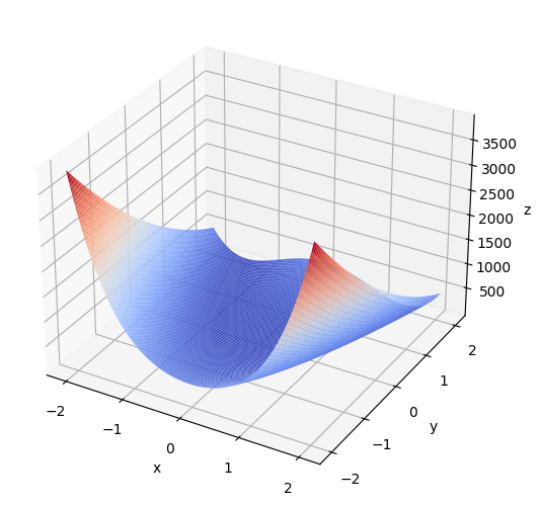
我们以一个二元函数的寻优为例介绍如何实现遗传算法。
例 9.1 求下面这个函数的极值:
$$F(x, y) = 100(y - x^2)^2 + (1 - x)^2 \tag{5.1.1}$$
首先,我们定义函数并给出绘图方法:
def F(x, y):
return 100.0 * (y - x ** 2.0) ** 2.0 + (1 - x) ** 2.0 # 以香蕉函数为例
def plot_3d(ax):
X = np.linspace(*X_BOUND, 100)
Y = np.linspace(*Y_BOUND, 100)
X, Y = np.meshgrid(X, Y)
Z = F(X, Y)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.pause(3)
plt.show()
函数图像如图所示:
执行遗传算法的第一步是进行编码并初始化种群,随后评估种群适应度。而评估适应度的过程中需要对编码后的算子进行解码,因此,给出解码方法和适应度评估函数:
def get_fitness(pop):
x, y = translateDNA(pop)
pred = F(x, y)
return pred
# return pred - np.min(pred)+1e-3 # 求最大值时的适应度
# return np.max(pred) - pred + 1e-3 # 求最小值时的适应度,通过这一步 fitness 的范围为[0, np.max(pred)-np.min(pred)]
def translateDNA(pop):
# pop 表示种群矩阵,一行表示一个二进制编码表示的 DNA,矩阵的行数为种群数目
x_pop = pop[:, 0:DNA_SIZE] # 前 DNA_SIZE 位表示 X
y_pop = pop[:, DNA_SIZE:] # 后 DNA_SIZE 位表示 Y
x = x_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0]
y = y_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]
return x, y
在迭代过程中,需要不断进行交叉变异等操作。这里给出变异操作的代码:
def mutation(child, MUTATION_RATE=0.003):
if np.random.rand() < MUTATION_RATE: # 以 MUTATION_RATE 的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE) # 随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point] ^ 1 # 将变异点的二进制为反转
交叉操作的代码如下
def crossover_and_mutation(pop, CROSSOVER_RATE=0.8):
new_pop = []
for father in pop: # 遍历种群中的每一个个体,将该个体作为父亲
child = father # 孩子先得到父亲的全部基因(这里我把一串二进制串的那些 0,1 称为基因)
if np.random.rand() < CROSSOVER_RATE: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] # 再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE * 2) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
mutation(child) # 每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
最终,会对种群进行自然选择,留下适应度高的部分。自然选择的代码形如:
def select(pop, fitness):
# nature selection wrt pop's fitness
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=(fitness) / (fitness.sum()))
return pop[idx]
完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
DNA_SIZE = 24
POP_SIZE = 80
CROSSOVER_RATE = 0.6
MUTATION_RATE = 0.01
N_GENERATIONS = 100
X_BOUND = [-2.048, 2.048]
Y_BOUND = [-2.048, 2.048]
def F(x, y):
return 100.0 * (y - x ** 2.0) ** 2.0 + (1 - x) ** 2.0 # 以香蕉函数为例
def plot_3d(ax):
X = np.linspace(*X_BOUND, 100)
Y = np.linspace(*Y_BOUND, 100)
X, Y = np.meshgrid(X, Y)
Z = F(X, Y)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.pause(3)
plt.show()
def get_fitness(pop):
x, y = translateDNA(pop)
pred = F(x, y)
return pred
# return pred - np.min(pred)+1e-3 # 求最大值时的适应度
# return np.max(pred) - pred + 1e-3 # 求最小值时的适应度,通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)]
def translateDNA(pop): # pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
x_pop = pop[:, 0:DNA_SIZE] # 前DNA_SIZE位表示X
y_pop = pop[:, DNA_SIZE:] # 后DNA_SIZE位表示Y
x = x_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0]
y = y_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]
return x, y
def crossover_and_mutation(pop, CROSSOVER_RATE=0.8):
new_pop = []
for father in pop: # 遍历种群中的每一个个体,将该个体作为父亲
child = father # 孩子先得到父亲的全部基因(这里我把一串二进制串的那些0,1称为基因)
if np.random.rand() < CROSSOVER_RATE: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] # 再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE * 2) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
mutation(child) # 每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
def mutation(child, MUTATION_RATE=0.003):
if np.random.rand() < MUTATION_RATE: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE) # 随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point] ^ 1 # 将变异点的二进制为反转
def select(pop, fitness): # nature selection wrt pop's fitness
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=(fitness) / (fitness.sum()))
return pop[idx]
def print_info(pop):
fitness = get_fitness(pop)
max_fitness_index = np.argmax(fitness)
print("max_fitness:", fitness[max_fitness_index])
x, y = translateDNA(pop)
print("最优的基因型:", pop[max_fitness_index])
print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))
print(F(x[max_fitness_index], y[max_fitness_index]))
if __name__ == "__main__":
fig = plt.figure()
ax = Axes3D(fig)
plot_3d(ax)
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 2)) # matrix (POP_SIZE, DNA_SIZE)
for _ in range(N_GENERATIONS): # 迭代N代
x, y = translateDNA(pop)
if 'sca' in locals():
sca.remove()
sca = ax.scatter(x, y, F(x, y), c='black', marker='o')
plt.show()
plt.pause(0.1)
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
fitness = get_fitness(pop)
pop = select(pop, fitness) # 选择生成新的种群
print_info(pop)
plot_3d(ax)
最终解得极值点出现在 $(x, y) = (2.04287866180412, -1.9751059526864263)$,极值为 $3781.442624151466$。
事实上,在第三章中我们其实也见到过,Python 的 scikit-opt 库也可以实现遗传算法。这里我们以两个案例介绍 sko 中遗传算法的使用。
例 9.2 求下面这个函数的极值:
$$ F(x, y) = x^2 + y^2 + \sin(x) + (1 - 0.001)x^2 \tag{5.1.2}$$
代码如下:
import numpy as np
from sko.GA import GA
def schaffer(p):
'''This function has plenty of local minimum, with strong shocks
global minimum at (0,0) with value 0'''
x1, x2 = p
x = np.square(x1) + np.square(x2)
return 0.5 + (np.square(np.sin(x)) - 0.5) / np.square(1 + 0.001 * x)
ga = GA(func=schaffer, n_dim=2, size_pop=50, max_iter=800, prob_mut=0.001, lb=[-1, -1], ub=[1, 1], precision=1e-7)
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)
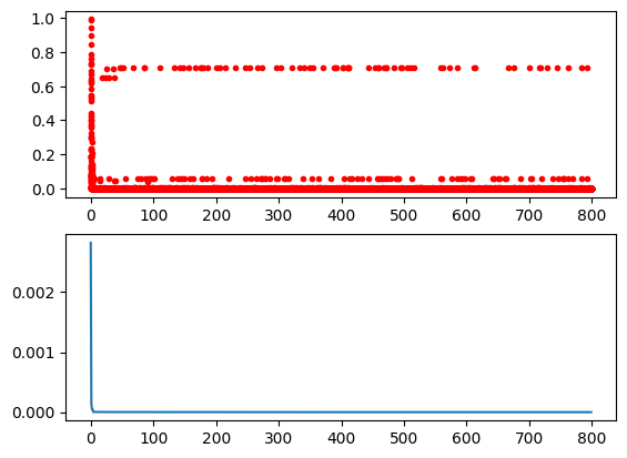
最终搜索到的最优解为 $[0,0]$。在迭代过程中的损失函数曲线也可以进行绘制:
import pandas as pd
import matplotlib.pyplot as plt
Y_history = pd.DataFrame(ga.all_history_Y)
fig, ax = plt.subplots(2, 1)
ax[0].plot(Y_history.index, Y_history.values, '.', color='red')
Y_history.min(axis=1).cummin().plot(kind='line')
plt.show()
所得到的适应度函数随迭代轮次的变化曲线如图所示:
例 9.3 利用遗传算法解 TSP 问题
我们可以先创建数据点的横纵坐标,并定义目标函数为回路的距离之和:
import numpy as np
from scipy import spatial
import matplotlib.pyplot as plt
num_points = 50
points_coordinate = np.random.rand(num_points, 2) # generate coordinate of points
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean')
def cal_total_distance(routine):
'''The objective function. input routine, return total distance.
cal_total_distance(np.arange(num_points))'''
num_points, = routine.shape
return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])
在 sko 中,有专门用于解决 TSP 问题的接口 GA_TSP 来通过遗传算法解决 TSP 问题。例如,我们看到下面的代码:
from sko.GA import GA_TSP
ga_tsp = GA_TSP(func=cal_total_distance, n_dim=num_points, size_pop=50, max_iter=500, prob_mut=1)
best_points, best_distance = ga_tsp.run()
fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([best_points, [best_points[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
ax[1].plot(ga_tsp.generation_best_Y)
plt.show()
最终得到的 TSP 回路路径与适应度函数变化曲线如图所示:
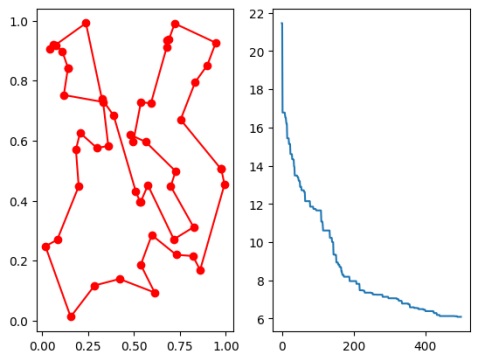
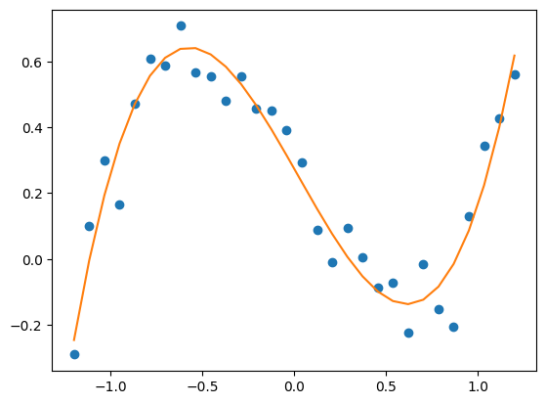
例 9.4 使用遗传算法进行数据拟合
我们随机生成一组数据点:
x_true = np.linspace(-1.2, 1.2, 30)
y_true = x_true ** 3 - x_true + 0.4 * np.random.rand(30)
plt.plot(x_true, y_true, 'o')
我们使用 sko 库中的遗传算法(GA) 进行拟合:
def f_fun(x, a, b, c, d):
return a * x ** 3 + b * x ** 2 + c * x + d
def obj_fun(p):
a, b, c, d = p
residuals = np.square(f_fun(x_true, a, b, c, d) - y_true).sum()
return residuals
nga = GA(func=obj_fun, n_dim=4, size_pop=100, max_iter=500, lb=[-2] * 4, ub=[2] * 4)
best_params, residuals = ga.run()
print('best_x:', best_params, '\n', 'best_y:', residuals)
y_predict = f_fun(x_true, *best_params)
fig, ax = plt.subplots()
ax.plot(x_true, y_true, 'o')
ax.plot(x_true, y_predict, '-')
plt.show()
# best_x: [ 0.93360083 -0.0612649 -0.98437051 0.27416942] best_y: [0.2066883]
5.2 粒子群算法理论与实现
5.3.1 粒子群算法
不知各位是否会注意到,鸟群例如大雁在飞行的时候它们的飞行方向除了受到环境的影响,还会受到其他大雁的影响,从而使群体中每一只大雁的飞行轨迹都整齐划一。而当一只鸟飞离鸟群去寻找栖息地的时候,它不仅要考虑自身运动方向和周围环境,还会从其他优秀的个体的飞行轨迹去模仿学习经验(当然它自己也可能被其它鸟模仿)。这一过程揭示了鸟群运动过程中的两类重要的知识:自我智慧和群体智慧。
现在假设一群鸟在一块有食物的区域内,它们都瞎了都不知道食物在哪里,但知道当前位置与食物的距离。最简单的方法就是搜寻目前离食物最近的鸟的区域。那我现在把这个区域看做是函数的搜索空间,每个鸟被抽象为一个粒子(物理意义上的质点),每个粒子有一个适应度和速度描述飞行方向和距离。粒子通过分析当前最优粒子在解空间中的运动过程去搜索最优解。设微粒群体规模为 $N$,其中每个微粒在 $D$ 维空间中的坐标位置可表示为 $X{i}=(x{i,1},x{i,2},…,x{i,D})$,微粒 i 的速度定义为每次迭代中微粒移动的距离,表示为 $Vi=(v{i,1},v{i,2},…,v{i,D})$,$Pi$ 表示微粒 $i$ 所经历的最好位置,$P_g$ 为群体中所有微粒所经过的最好位置,则微粒 $i$ 在第 $d$ 维子空间中的飞行速度 $v{i,d}$ 根据下式进行调整:
$$ v{i,d}^{t+1} = w \cdot v{i,d}^{t} + c1 \cdot \text{Rand}() \cdot (p{i,d}^t - x{i,d}^{t}) + c_2 \cdot \text{Rand}() \cdot (p{g,d}^t - x_{i,d}^{t}) \tag{5.2.1}$$
在这个过程中,每次运动的时间间隔被视作单位 $1$,那么速度实际上也可以用于描述下一个时间间隔的移动方向和移动距离。
$$ x{i,d}^{t+1} = x{i,d}^{t} + v_{i,d}^{t+1} \tag{5.2.2}$$
第一项为微粒先前速度乘一个权值进行加速,表示微粒对当前自身速度状态的信任,依据自身的速度进行惯性运动,因此称这个权值为惯性权值。第二项为微粒当前位置与自身最优位置之间的距离,为认知部分,表示微粒本身的思考,即微粒的运动来源于自己经验的部分。第三项为微粒当前位置与群体最优位置之间的距离,为社会部分,表示微粒间的信息共享与相互合作,即微粒的运动中来源于群体中其他微粒经验的部分。
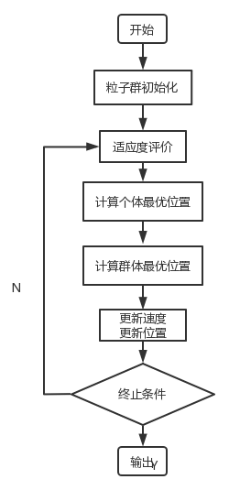
粒子群算法基本流程:
- 初始化:随机初始化每一微粒的位置和速度。
- 评估:依据适应度函数计算每个微粒的适应度值,以作为判断每一微粒之好坏。
- 寻找个体最优解:找出每一微粒到目前为止的搜寻过程中最佳解,这个最佳解称为 Pbest。
- 寻找群体最优解:找出所有微粒到目前为止所搜寻到的整体最佳解,此最佳解称之为 Gbest。
- 更新每一微粒的速度与位置。
- 回到步骤 2 继续执行,直到获得一个令人满意的结果或符合终止条件为止。
粒子群算法的工作流程如图 9.7 所示:
5.2.2 粒子群算法的实现
例 9.5 求下面这个函数的极值:
$$F(x, y) = 3\cos(x y) + x + y^2 \tag{9.2.3}
$$ 我们可以先通过它的图像来观察它的性质:
import numpy as np
import matplotlib.pyplot as plt
X = np.arange(-4 ,4 ,0.01)
Y = np.arange(-4 ,4 ,0.01)
x, y = np.meshgrid(X ,Y)
Z = 3*np.cos(x * y) + x + y**2
# 作图
fig = plt.figure(figsize=(10,15))
ax3 = plt.axes(projection = "3d")
ax3.plot_surface(x,y,Z ,cmap = "rainbow")
plt.show()
得到图像如图9.8 所示:
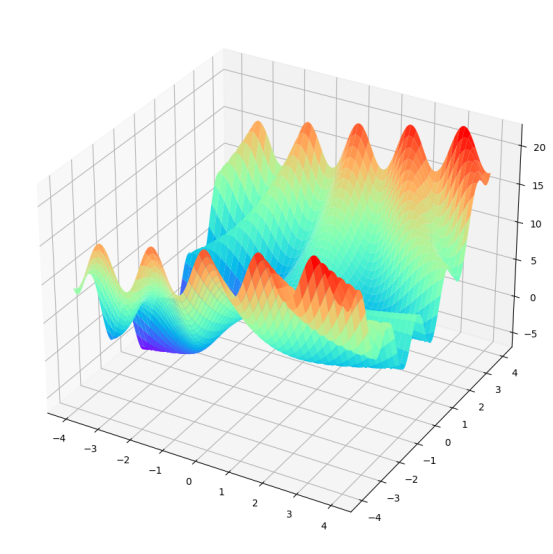
从图中可以看到函数有多个极值点,我们使用粒子群算法找到函数的全局最优点。对上述过程进行复现的完整代码如下:
import numpy as np
# 初始化种群,群体规模,每个粒子的速度和规模
N = 100 # 种群数目
D = 2 # 维度
T = 200 # 最大迭代次数
c1 = c2 = 1.5 # 个体学习因子与群体学习因子
w_max = 0.8 # 权重系数最大值
w_min = 0.4 # 权重系数最小值
x_max = 4 # 每个维度最大取值范围,如果每个维度不一样,那么可以写一个数组,下面代码依次需要改变
x_min = -4 # 同上
v_max = 1 # 每个维度粒子的最大速度
v_min = -1 # 每个维度粒子的最小速度
# 定义适应度函数
def func(x):
return 3 * np.cos(x[0] * x[1]) + x[0] + x[1] ** 2
# 初始化种群个体
x = np.random.rand(N, D) * (x_max - x_min) + x_min # 初始化每个粒子的位置
v = np.random.rand(N, D) * (v_max - v_min) + v_min # 初始化每个粒子的速度
# 初始化个体最优位置和最优值
p = x # 用来存储每一个粒子的历史最优位置
p_best = np.ones((N, 1)) # 每行存储的是最优值
for i in range(N): # 初始化每个粒子的最优值,此时就是把位置带进去,把适应度值计算出来
p_best[i] = func(x[i, :])
# 初始化全局最优位置和全局最优值
g_best = 100 #设置真的全局最优值
gb = np.ones(T) # 用于记录每一次迭代的全局最优值
x_best = np.ones(D) # 用于存储最优粒子的取值
# 按照公式依次迭代直到满足精度或者迭代次数
for i in range(T):
for j in range(N):
# 个更新个体最优值和全局最优值
if p_best[j] > func(x[j,:]):
p_best[j] = func(x[j,:])
p[j,:] = x[j,:].copy()
# p_best[j] = func(x[j,:]) if func(x[j,:]) < p_best[j] else p_best[j]
# 更新全局最优值
if g_best > p_best[j]:
g_best = p_best[j]
x_best = x[j,:].copy() # 一定要加 copy,否则后面 x[j,:]更新也会将 x_best 更新
# 计算动态惯性权重
w = w_max - (w_max - w_min) * i / T
# 更新位置和速度
v[j, :] = w * v[j, :] + c1 * np.random.rand(1) * (p[j, :] - x[j, :]) + c2 * np.random.rand(1) * (x_best - x[j, :])
x[j, :] = x[j, :] + v[j, :]
# 边界条件处理
for ii in range(D):
if (v[j, ii] > v_max) or (v[j, ii] < v_min):
v[j, ii] = v_min + np.random.rand(1) * (v_max - v_min)
if (x[j, ii] > x_max) or (x[j, ii] < x_min):
x[j, ii] = x_min + np.random.rand(1) * (x_max - x_min)
# 记录历代全局最优值
gb[i] = g_best
print("最优值为", gb[T - 1],"最优位置为",x_best)
plt.plot(range(T),gb)
plt.xlabel("迭代次数")
plt.ylabel("适应度值")
plt.title("适应度进化曲线")
plt.show()
可以得到适应度的进化曲线如图9.9 所示:
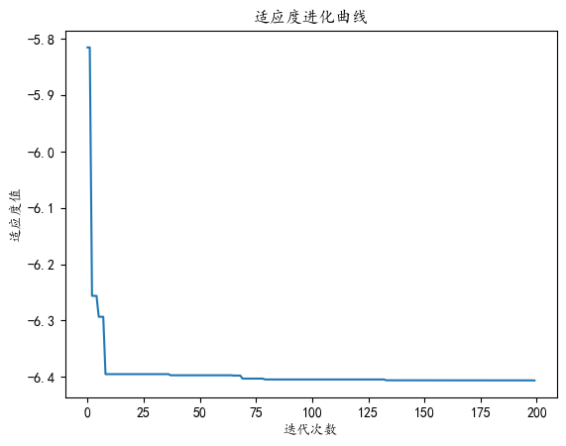
最终得到的搜索结果为最优值为 $-6.4063965702604575$ 最优位置为 $[-3.99999512 -0.74624737]$
同样的,在 sko 中有 PSO 方法提供了粒子群算法的接口。例如,下面两个例子都可以使用 PSO 接口进行求解。
例 9.6 求下面这个函数的极值:
$$ F(x) = x1^2 + (x_2 - 0.05)^2 + x_3^2, \quad x{3} \geqslant 0.05 \tag{5.2.4}$$
使用 sko.PSO 提供的 PSO 方法解决这个问题的代码如下:
from sko.PSO import PSO
def demo_func(x):
x1, x2, x3 = x
return x1 ** 2 + (x2 - 0.05) ** 2 + x3 ** 2
pso = PSO(func=demo_func, dim=3, pop=40, max_iter=150, lb=[0, -1, 0.5], ub=[1, 1, 1], w=0.8, c1=0.5, c2=0.5)
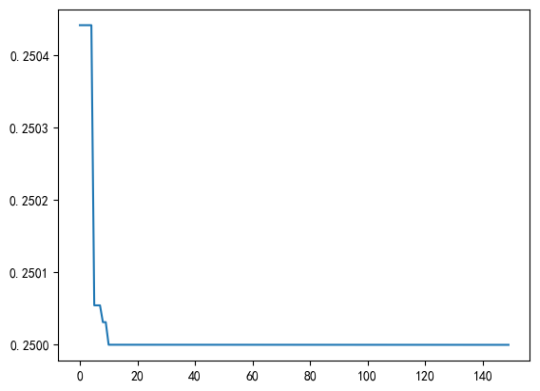
pso.run()
print('best_x is ', pso.gbest_x, 'best_y is', pso.gbest_y)
plt.plot(pso.gbest_y_hist)
plt.show()
# best_x is [0. 0.05 0.5 ] best_y is [0.25]
例 9.7 利用粒子群算法解 TSP 问题
与遗传算法类似,粒子群算法也提供了针对 TSP 问题的接口。完整代码如下:
from sko.PSO import PSO_TSP
from scipy import spatial
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean')
def cal_total_distance(routine):
'''The objective function. input routine, return total distance.
cal_total_distance(np.arange(num_points))'''
num_points, = routine.shape
return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])
pso_tsp = PSO_TSP(func=cal_total_distance, n_dim=num_points, size_pop=200, max_iter=800, w=0.8, c1=0.1, c2=0.1)
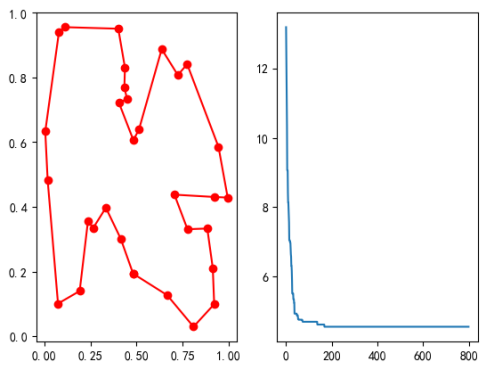
best_points, best_distance = pso_tsp.run()
print('best_distance', best_distance)
fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([best_points, [best_points[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
ax[1].plot(pso_tsp.gbest_y_hist)
plt.show()
最优距离为 $4.5485$,得到的结果如图所示:
5.3 蚁群算法理论与实现
5.2.1 蚁群算法
蚁群算法(Ant colony algorithm)是 20 世纪 90 年代初意大利学者 M.Dorigo,V.Maniezzo,A.Colorni 等从生物进化的机制中受到启发,通过模拟自然界蚂蚁搜索路径的行为提出来的一种新型的模拟进化算法。蚂蚁在运动过程中,能够在它所经过的路径上留下一种称之为外激素(pheromone)的物质进行信息传递,而且蚂蚁在运动过程中能够感知这种物质,并以此指导自己的运动方向,因此由大量蚂蚁组成的蚁群集体行为便表现出一种信息正反馈现象:某一路径上走过的蚂蚁越多,则后来者选择该路径的概率就越大。最优路径上的激素浓度越来越大,而其它的路径上激素浓度却会随着时间的流逝而消减。最终整个蚁群会找出最优路径。
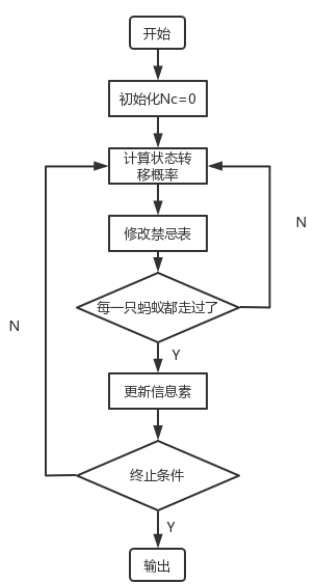
蚁群算法的规则如下:
- 初始化:为每条边上的初始信息素和蚂蚁进行赋值。
- 如果满足算法外循环的停止规则则停止计算并输出最优解;否则蚂蚁们统统从起点出发,将走过的路径添加到集合中。
- 对每一只蚂蚁,按照信息素浓度分配各个路径的概率,并选择路径同时留下信息素。 分配规则如下:$$ p{i,j} = \frac{\tau{i,j}^{\alpha} \cdot \eta{i,j}^{\beta}}{\sum{k=0}^{n-1} \tau{ik}^{\alpha} \cdot \eta{ik}^{\beta}} \tag{5.2.5}$$ 其中,$\tau{i,j}$ 是从节点 $i$ 到节点 $j$ 的信息素浓度,$\eta{i,j}$ 是启发式因子,通常是距离的倒数,$\alpha$ 和 $\beta$ 是参数。
- 按照一定规则对最短路径上的信息素增强,其他路径上的信息素进行挥发。定义最短路径为 $W$,挥发的规则形如:$$ \tau{i,j} \leftarrow (1 - \rho) \tau{i,j} + \Delta \tau{i,j} \tag{5.2.6}$$ 其中,$\rho$ 是挥发率,$\Delta \tau{i,j}$ 是路径 $i$ 到 $j$ 上新增的信息素量。
注意:蚁群算法的过程中边上信息素的一些状态和蚂蚁的行进信息可以用一个表格(数组)存储起来,这个表叫禁忌表。
蚁群算法的流程如图9.12 所示:
5.2.2 蚁群算法的实现
我们可以用面向对象的方式提供一种蚁群算法的实现:
import numpy as np
import matplotlib.pyplot as plt
class ACO:
def __init__(self, parameters):
# 初始化
self.NGEN = parameters[0] # 迭代的代数
self.pop_size = parameters[1] # 种群大小
self.var_num = len(parameters[2]) # 变量个数
self.bound = [] # 变量的约束范围
self.bound.append(parameters[2])
self.bound.append(parameters[3])
self.pop_x = np.zeros((self.pop_size, self.var_num)) # 所有蚂蚁的位置
self.g_best = np.zeros((1, self.var_num)) # 全局蚂蚁最优的位置
# 初始化第 0 代初始全局最优解
temp = -1
for i in range(self.pop_size):
for j in range(self.var_num):
self.pop_x[i][j] = np.random.uniform(self.bound[0][j], self.bound[1][j])
fit = self.fitness(self.pop_x[i])
if fit > temp:
self.g_best = self.pop_x[i]
temp = fit
def fitness(self, ind_var):
""“个体适应值计算""“
x1 = ind_var[0]
x2 = ind_var[1]
x3 = ind_var[2]
y = 4*x1 ** 2 + 2*x2 + x3 ** 3
return y
def update_operator(self, gen, t, t_max):
""“更新算子:根据概率更新下一时刻的位置""“
rou = 0.8 # 信息素挥发系数
Q = 1 # 信息释放总量
lamda = 1 / gen
pi = np.zeros(self.pop_size)
for i in range(self.pop_size):
for j in range(self.var_num):
pi[i] = (t_max - t[i]) / t_max
# 更新位置
if pi[i] < np.random.uniform(0, 1):
self.pop_x[i][j] = self.pop_x[i][j] + np.random.uniform(-1, 1) * lamda
else:
self.pop_x[i][j] = self.pop_x[i][j] + np.random.uniform(-1, 1) * (
self.bound[1][j] - self.bound[0][j]) / 2
# 越界保护
if self.pop_x[i][j] < self.bound[0][j]:
self.pop_x[i][j] = self.bound[0][j]
if self.pop_x[i][j] > self.bound[1][j]:
self.pop_x[i][j] = self.bound[1][j]
# 更新 t 值
t[i] = (1 - rou) * t[i] + Q * self.fitness(self.pop_x[i])
# 更新全局最优值
for i in range(self.pop_size):
if self.fitness(self.pop_x[i]) > self.fitness(self.g_best):
self.g_best = self.pop_x[i].copy()
t_max = np.max(t)
return t_max, t
def main(self):
popobj = []
best = np.zeros((1, self.var_num))[0]
for gen in range(1, self.NGEN + 1):
if gen == 1:
tmax, t = self.update_operator(gen, np.array(list(map(self.fitness, self.pop_x))),
np.max(np.array(list(map(self.fitness, self.pop_x)))))
else:
tmax, t = self.update_operator(gen, t, tmax)
print('############ Generation {} ############'.format(str(gen)))
print(self.g_best)
print(self.fitness(self.g_best))
if self.fitness(self.g_best) > self.fitness(best):
best = self.g_best.copy()
popobj.append(self.fitness(best))
print('最好的位置:{}'.format(best))
print('最大的函数值:{}'.format(self.fitness(best)))
print("---- End of (successful) Searching ----")
plt.figure()
plt.title("Figure1")
plt.xlabel("iterators", size=14)
plt.ylabel("fitness", size=14)
t = [t for t in range(1, self.NGEN + 1)]
plt.plot(t, popobj, color='b', linewidth=2)
plt.show()
if __name__ == '__main__':
NGEN = 100
popsize = 50
low = [1, 1, 1]
up = [30, 30, 30]
parameters = [NGEN, popsize, low, up]
aco = ACO(parameters)
aco.main()
如果使用 sko 工具,sko.ACA 也提供了蚁群算法的接口。蚁群算法在解决 TSP 问题中有着重要作用,例如,使用下面的代码利用蚁群算法解决 TSP 问题:
import numpy as np
from scipy import spatial
import matplotlib.pyplot as plt
num_points = 50
points_coordinate = np.random.rand(num_points, 2) # generate coordinate of points
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean')
def cal_total_distance(routine):
'''The objective function. input routine, return total distance.
cal_total_distance(np.arange(num_points))'''
num_points, = routine.shape
return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])
from sko.ACA import ACA_TSP
aca = ACA_TSP(func=cal_total_distance, n_dim=num_points,
size_pop=50, max_iter=200,
distance_matrix=distance_matrix)
best_points, best_distance = aca.run()
print(best_points)
print(best_distance)
fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([best_points, [best_points[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
ax[1].plot(aca.generation_best_Y)
plt.show()
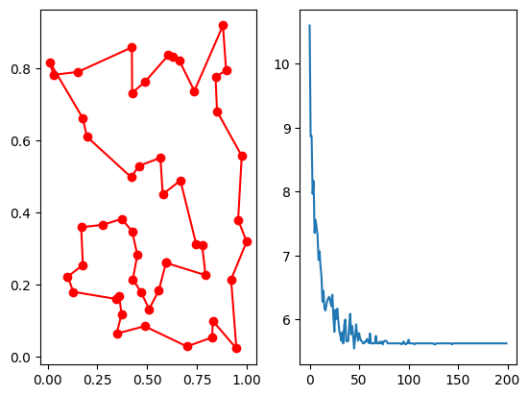
5.4 模拟退火算法理论与实现
模拟退火算法由 Kirkpatrick 等提出,能有效的解决局部最优解问题。它不同于前面基于生物的进化和群体智能,它是基于物理学定律提出的方法。
5.4.1 模拟退火算法
模拟退火算法(Simulated Annealing, SA)的思想借鉴于固体的退火原理,当固体的温度很高的时候,内能比较大,固体的内部粒子处于快速无序运动,当温度慢慢降低的过程中,固体的内能减小,粒子的慢慢趋于有序,最终,当固体处于常温时,内能达到最小,此时,粒子最为稳定。模拟退火算法便是基于这样的原理设计而成。
模拟退火算法来源于晶体冷却的过程,如果固体不处于最低能量状态,给固体加热再冷却,随着温度缓慢下降,固体中的原子按照一定形状排列,形成高密度、低能量的有规则晶体,对应于算法中的全局最优解。而如果温度下降过快,可能导致原子缺少足够的时间排列成晶体的结构,结果产生了具有较高能量的非晶体,这就是局部最优解。因此就可以根据退火的过程,给其在增加一点能量,然后再冷却,如果增加能量,跳出了局部最优解,本次退火就是成功的。
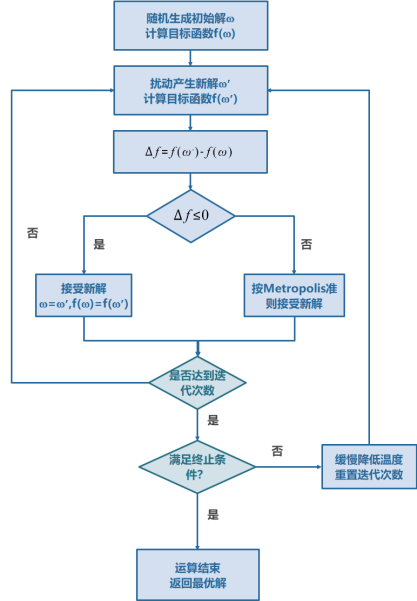
模拟退火算法包含两个部分即 Metropolis 准则和退火过程。Metropolis 准则以概率来接受新状态,而不是使用完全确定的规则,称为 Metropolis 准则,计算量较低。从某一个解到新解本质上是衡量其能量变化,若能量向递减的方向跃迁则接受这一次迭代,若能量反而增大,并不是一定拒绝而是以一定的采样概率接受。这一概率值满足 Metropolis 定义:
$$ P = \exp\left(-\frac{E{new} - E{old}}{T}\right) \tag{5.4.1}$$
直接使用 Metropolis 算法可能会导致寻优速度太慢,以至于无法实际使用,为了确保在有限的时间收敛,必须设定控制算法收敛的参数,在上面的公式中,可以调节的参数就是 $T$,$T$ 如果过大,就会导致退火太快,达到局部最优值就会结束迭代,如果取值较小,则计算时间会增加,实际应用中采用退火温度表,在退火初期采用较大的 $T$ 值,随着退火的进行,逐步降低。
模拟退火的过程如图 9.14 所示:
注意:速度上模拟退火和粒子群都很快,但模拟退火略快一些,比遗传更快,蚁群的速度是最慢的。但粒子群求解大规模函数极值的时候容易碰到边界陷入的情况。模拟退火则相对比较稳定一些。
5.4.2 模拟退火算法的实现
例 9.8 求下面这个函数的极值:
$$ y = x^3 - 60x^2 - 4x + 6 \tag{5.4.2}$$
使用 python 对模拟退火算法进行编程的代码如下:
import numpy as np
import math
def aimFunction(x):
y = x ** 3 - 60 * x ** 2 - 4 * x + 6
return y
x = [i / 10 for i in range(1000)]
y = [0 for i in range(1000)]
for i in range(1000):
y[i] = aimFunction(x[i])
plt.plot(x, y)
plt.show()
T = 1000 # initiate temperature
Tmin = 10 # minimum value of temperature
x = np.random.uniform(low=0, high=100) # initiate x
k = 50 # times of internal circulation
y = 0 # initiate result
t = 0 # time
while T >= Tmin:
for i in range(k):
# calculate y
y = aimFunction(x)
# generate a new x in the neighboorhood of x by transform function
xNew = x + np.random.uniform(low=-0.055, high=0.055) * T
if (0 <= xNew and xNew <= 100):
yNew = aimFunction(xNew)
if yNew - y < 0:
x = xNew
else:
# metropolis principle
p = math.exp(-(yNew - y) / T)
r = np.random.uniform(low=0, high=1)
if r < p:
x = xNew
t += 1
T = 1000 / (1 + t) #降温函数,也可使用 T=0.9T
print(x, aimFunction(x))
# 39.78060332087924 -32150.24487975278
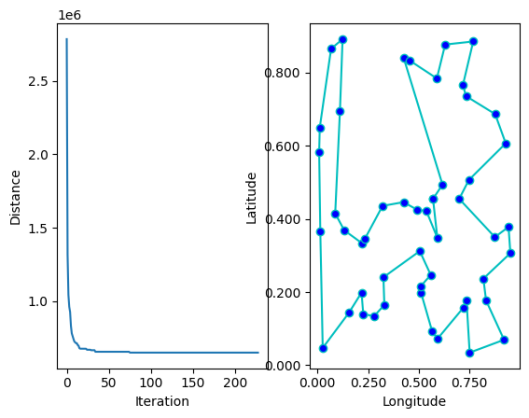
例 9.9 使用模拟退火算法解决 TSP 问题
使用 sko 中提供的模拟退火算法接口解一个 TSP 问题的代码如下:
from sko.SA import SA_TSP
nsa_tsp = SA_TSP(func=cal_total_distance, x0=range(num_points), T_max=800, T_min=1, L=1000)
best_points, best_distance = sa_tsp.run()
print(best_points, best_distance, cal_total_distance(best_points))
fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([best_points, [best_points[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(sa_tsp.best_y_history)
ax[0].set_xlabel("Iteration")
ax[0].set_ylabel("Distance")
ax[1].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], marker='o', markerfacecolor='b', color='c', linestyle='-')
ax[1].set_xlabel("Longitude")
ax[1].set_ylabel("Latitude")
plt.show()
得到结果如图所示:
5.5 使用 scikit-opt 实现智能优化算法
5.5.1 智能优化算法分类
智能优化算法受到人类智能、生物群体社会性或自然现象规律的启发,主要包括以下几种类型:
进化类算法:
- 遗传算法:模仿自然界生物进化机制。
- 差分进化算法:通过群体个体间的合作与竞争来优化搜索。
- 免疫算法:模拟生物免疫系统学习和认知功能。
群体智能算法:
- 蚁群算法:模拟蚂蚁集体寻径行为。
- 粒子群算法:模拟鸟群和鱼群群体行为。
除了以上常见的算法外,还有许多其他群体智能优化算法,例如:萤火虫算法、布谷鸟算法、蝙蝠算法、狼群算法、烟花算法、合同网协议算法等等。
- 模拟退火算法:源于固体物质退火过程。
- 禁忌搜索算法:模拟人类智力记忆过程。
- 神经网络算法:模拟动物神经网络行为特征。
5.5.2 Scikit-opt 使用方法简介
Scikit-opt 封装了 7 种启发式算法,分别是差分进化算法、遗传算法、粒子群算法、模拟退火算法、蚁群算法、鱼群算法和免疫优化算法。
在探索智能优化算法之前,首先我们需要先安装 scikit-opt 库。
pip install scikit-opt
接下来我们来学习如何利用 Scikit-opt 库实现上述的七种算法,下面是一些简单的案例:
1. 差分进化算法
例 9.10 解下面的优化问题:
$$ \begin{align} \text{minimize}~&f(x{1}, x{2}, x{3}) = x{1}^{2} + x{2}^{2} + x{3}^{2}\ \text{s.t.}~&x{1}x{2} \geqslant 1\ &x{1}x{2} \leqslant 5\ &x{2} + x{3} = 1\ &0 \leqslant x{1}, x{2}, x_{3} \leqslant 5 \end{align} \tag{5.5.1}
$$
from sko.DE import DE
de = DE(func=obj_func, n_dim=3, size_pop=50, max_iter=800, lb=[0, 0, 0], ub=[5, 5, 5],
constraint_eq=constraint_eq, constraint_ueq=constraint_ueq)
best_x, best_y = de.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)
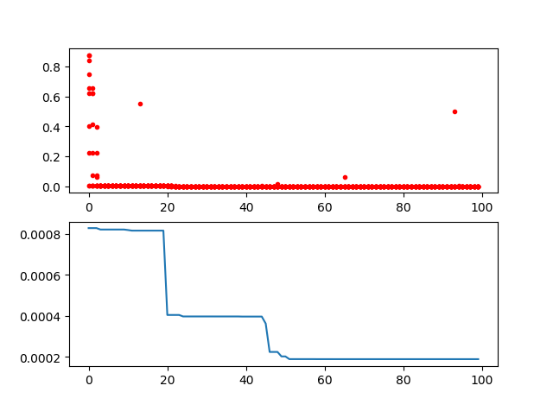
2. 遗传算法
例 9.11 解下面的优化问题:
$$ \text{minimize}~f(x{1}, x{2}, x{3}) = x{1}^{2} + (x{2} - 0.05)^{2} + x{3}^{2} \tag{5.5.2}
$$
from sko.GA import GA
def schaffer(p):
'''
这个函数有很多局部最小值,具有强烈的震荡
全局最小值在 (0,0) 处,值为 0
'''
x1, x2 = p
x = np.square(x1) + np.square(x2)
return 0.5 + (np.square(np.sin(x)) - 0.5) / np.square(1 + 0.001 * x)
ga = GA(func=schaffer, n_dim=2, size_pop=50, max_iter=800, prob_mut=0.001, lb=[-1, -1], ub=[1, 1], precision=1e-7)
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)
import pandas as pd
import matplotlib.pyplot as plt
Y_history = pd.DataFrame(ga.all_history_Y)
fig, ax = plt.subplots(2, 1)
ax[0].plot(Y_history.index, Y_history.values, '.', color='red')
Y_history.min(axis=1).cummin().plot(kind='line')
plt.show()
3. 粒子群算法
例 9.12 解下面的优化问题:
$$ \text{minimize}~f(x{1}, x{2}) = 0.5 + \frac{\sin^{2}\Big(x{1}^{2} + x{2}^{2}\Big) - 0.5}{\Big(1 + 0.001(x{1}^{2} + x{2}^{2})\Big)^{2}} \tag{5.5.3}
$$
def demo_func(x):
x1, x2, x3 = x
return x1 ** 2 + (x2 - 0.05) ** 2 + x3 ** 2
from sko.PSO import PSO
pso = PSO(func=demo_func, n_dim=3, pop=40, max_iter=150, lb=[0, -1, 0.5], ub=[1, 1, 1], w=0.8, c1=0.5, c2=0.5)
pso.run()
print('best_x is ', pso.gbest_x, 'best_y is', pso.gbest_y)
import matplotlib.pyplot as plt
plt.plot(pso.gbest_y_hist)
plt.show()
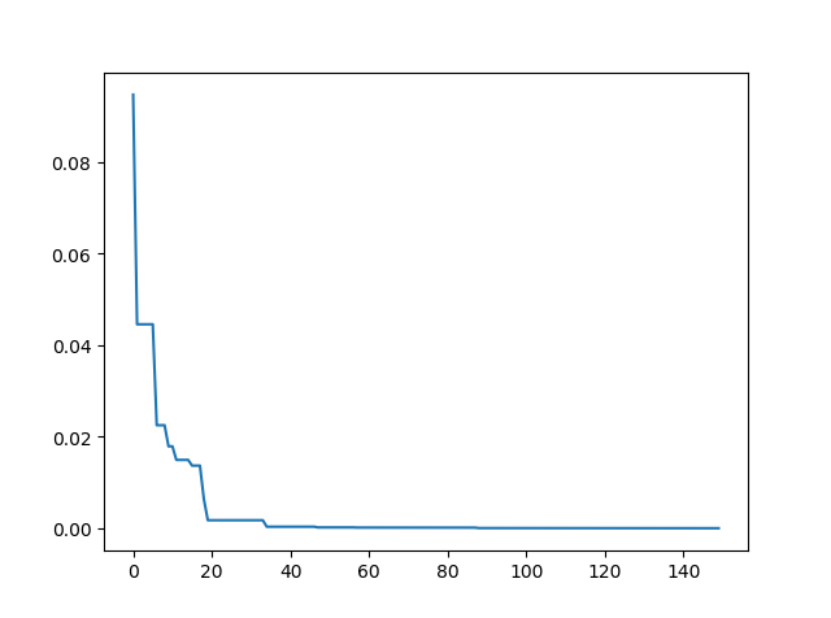
4. 模拟退火算法
例 9.13 解下面的优化问题:
from sko.SA import SA
sa = SA(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, L=300, max_stay_counter=150)
best_x, best_y = sa.run()
print('best_x:', best_x, 'best_y', best_y)
scikit-opt 还提供了三种模拟退火流派: Fast, Boltzmann 和 Cauchy.
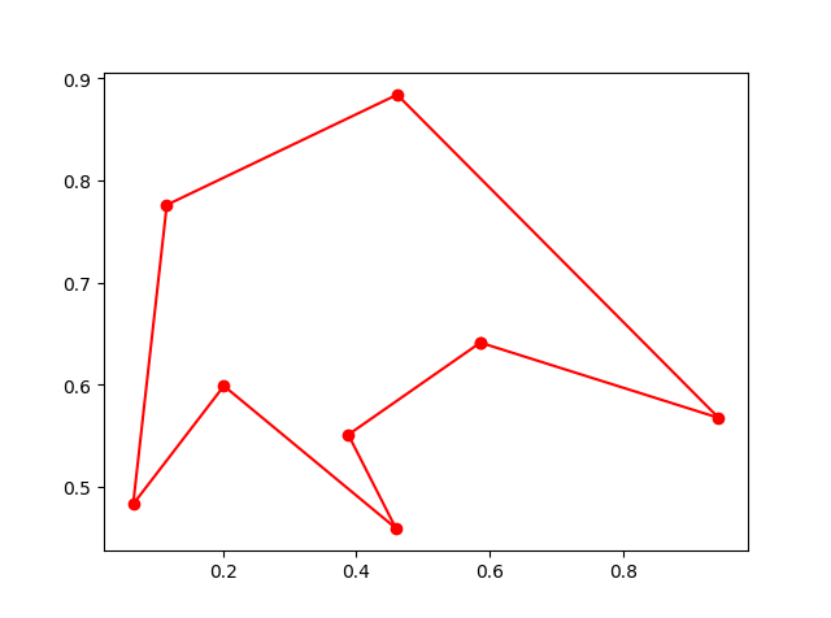
5.蚁群算法
例 9.14 解决TSP问题:
from sko.ACA import ACA_TSP
aca = ACA_TSP(func=cal_total_distance, n_dim=num_points,
size_pop=50, max_iter=200,
distance_matrix=distance_matrix)
best_x, best_y = aca.run()
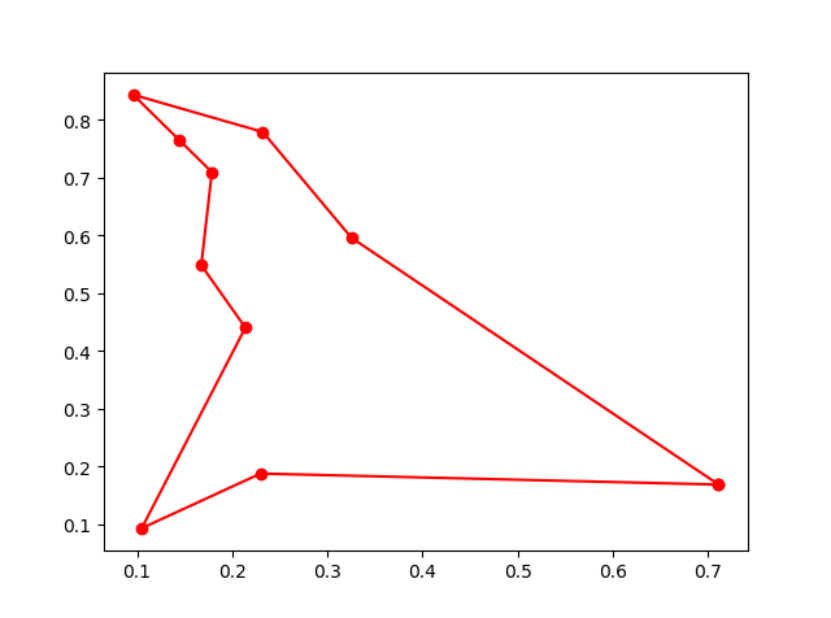
6. 免疫优化算法
例 9.15 解决TSP问题:
from sko.IA import IA_TSP
ia_tsp = IA_TSP(func=cal_total_distance, n_dim=num_points, size_pop=500, max_iter=800,
prob_mut=0.2,
T=0.7, alpha=0.95)
best_points, best_distance = ia_tsp.run()
print('best routine:', best_points, 'best_distance:', best_distance)
7. 人工鱼群算法
例 9.16 解下面的优化问题:
$$ \text{minimize}~f(x{1}, x{2}) = \frac{1}{x{1}^{2}} + x{1}^{2} + \frac{1}{x{2}^{2}} + x{2}^{2} \tag{5.5.4}
$$
from sko.AFSA import AFSA
def func(x):
x1, x2 = x
return 1 / x1 ** 2 + x1 ** 2 + 1 / x2 ** 2 + x2 ** 2
afsa = AFSA(func, n_dim=2, size_pop=50, max_iter=300,
max_try_num=100, step=0.5, visual=0.3,
q=0.98, delta=0.5)
best_x, best_y = afsa.run()
print(best_x, best_y)