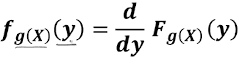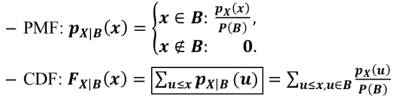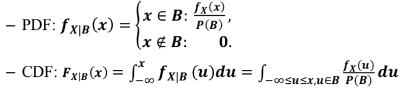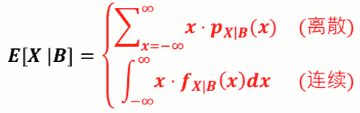• Week6 Week7 期望值 条件概率 失忆性
  • 6-2: 期望值 I (EXPECTATION)
    • 随机变量的函数之期望值
    • 期望值运算性质
    • 常见的随机变量函数期望值
    • 变异数 (variance)
    • Variance 便利算法
    • 常见离散分布之期望值/变异数
    • 几率推导奥义： 「凑」字诀
    • Quiz
• Week7
  • 7-1 期望值II
    • 随机变数函数 期望值
    • 常见连续分布的期望值/变异数
    • 期望值推导
  • 7.2 隨機變數之函數
    • 如何求 g(X)几率分布?
  • 7.3a 条件概率分布
  • 7.3a 失忆性 (Memoryless)
  • QUIZ

Week6 Week7 期望值 条件概率 失忆性

6-2: 期望值 I (EXPECTATION)

• 大数法则
  • 想知道某事件发生的机率?
  • 作很多次实验，记录实验中出现那个事件多少次。当实验次数接近无穷 多次时，这个比例就会越来越接近实际的机率!
  • P(A) = lim_N→∞ (N_A/N)
• 期望值 (Expectation)
  • 做随机实验时，我们很希望能有某种估算
  • 平均值是我们平常最常普遍的估算值
  • 作两次实验的平均值是? (X₁+X₂)/2 = ?
  • 不管我们做多少次实验，平均值都是一个随机变数，那不就 不能拿来估算?
  • 所幸!当做的实验次数趋近于无穷多时，这么多次的实验的平均值 会收敛到一个常数!我们就用它来当作这机率分布的估算值吧!
• 若考虑某机率分布，作实验很多次若随机实验之样本空间为 {1,2, ... ,n}, 作实验N次，记录各结果出现 次数，分别为N₁,N₂,...N_n
  • 平均值 (Mean): ∑_x=ⁿ₁ (x·Nₓ)/N
  • 根据大数法则 : ∑_x=ⁿ₁ x·P_X(x)
• Mean 值又称作期望值
  • μ_Y = E[Y]
  • 对离散随机变数 𝑿 而言，我们定义其期望值
    • E[X] = μ_X = ∑_x=^∞_-∞ x·P_X(x)
  • 期望值不等于随机会发生的值!
    • eg. P_X(1) = P_X(-1) = 1/2 => μ_X = 0 !!!

随机变量的函数之期望值

• 对于任一离散随机变量 X 而言，其 任意函数 g(X) 亦是一随机变量，亦有期望值
• g(X) 期望值定义为
  • E[ g(X) ] = ∑_x=^∞_-∞ g(x)·P_X(x)
  • 根随即变量的期望值公式相比，只是 x 变成了 g(x)

期望值运算性质

• E[ 3X² ] = ∑_x=^∞_-∞ 3x²·P_X(x)
  • = 3·∑_x=^∞_-∞ x²·P_X(x) = 3·E[X²]
  • 常数项可以提出来
• E[α·g(X)] = α·E[g(X)]
• E[α·g(X) + β·h(X) ] = α·E[g(X)] + β·E[h(X)]
• E[α] = α

常见的随机变量函数期望值

• X 的 n^th moment:
  • E[Xⁿ] = ∑_x=^∞_-∞ xⁿ·P_X(x)
  • Ex: E[X²] 是 X的 2^nd moment
• X 的变异数 (variance):
  • E[ (X-μ_X)² ]
  • 减去 期望值的 平方
• 全期望值公示
  • E[Y] = E[E(Y|X)]

变异数 (variance)

• Variance通常符号表示为 σ_X² = E[ (X-μ_X)² ]
• 变异数隐含关于随机变数 X 多「乱」的信息
• 变异数的开根号便是标准差 (standard deviation)
  • σ_X = √Variance
• 性质:
  • if a constant is added to all values of the variable, the variance is unchanged:
    • Var[X + a] = Var[X]
  • If all values are scaled by a constant, the variance is scaled by the square of that constant:
    • Var[aX] = a²Var[X]
• 双变量 期望值，Variance，见第8章

Variance 便利算法

• σ_X² = E[ (X-μ_X)² ]

  • = E[ X²-2μ_X·X+μ_X² ]
  • = E[X²] + E[-2μ_X·X] + E[ μ_X² ]
  • = E[X²] - 2μ_X·E[X] + μ_X²
  • = E[X²] - μ_X²

• => E[X²] = σ_X² + μ_X²

常见离散分布之期望值/变异数

• X~Bernouli(p) :
  • μ_X = 1·p + 0·(1-p) = p
  • σ_X² = E[X²] - μ_X² = ∑_x=¹₀ x²·p_X(x) - μ_X²
    • = 1²·p + 0²·(1-p) - p² = p(1-p)
• X~BIN(n,p) :
  • μ_X = np
  • σ_X² = np(1-p)
• X~GEO(p) :
  • μ_X = ∑_x=^∞₀ x· (1-p)^x-1·p = 1/p
  • σ_X² = E[X²] - μ_X² = (1-p)/p²
• X~PASKAL(k,p) :
  • μ_X = k/p
  • σ_X² = k(1-p)/p²
• X~POI(α) :
  • μ_X = α
  • σ_X² = α
• X~UNIF(a,b) :
  • μ_X = (a+b)/2
  • σ_X² = 1/12·(b-a)(b-a+2)

几率推导奥义： 「凑」字诀

• 以 X~POI(a) 为例
• X~POI(a) 概率公式是什么？
  • P_X(x) = (aˣ/x!)·e⁻ª , x=0,1,2,...
• 我们手上能利用的公式有哪些？
  • ∑_x=^∞₀ (aˣ/x!)·e⁻ª = 1
• 开始推导:

E[X] = ∑_x=^∞₀ x·(aˣ/x!)·e⁻ª

x 和 x！约分，变成 (x-1)! , 这样 ∑ 运算就不能包括 x=0了， 因为 阶乘对负数没有定义

E[X] = ∑_x=^∞₁ (aˣ/(x-1)!)·e⁻ª

使 a 的指数形式 和 阶乘 保持一致

E[X] = a·∑_x=^∞₁ (aˣ⁻¹/(x-1)!)·e⁻ª

令 x' = x-1

E[X] = a· ∑_x'=^∞₀ (aˣ^'/x'!)·e⁻ª = a·1 = a

σ_X² = E[X²] - μ_X² = E[X²] - a²

和 E[X] 类似， 可以推导处 E[X²] = a² + a , 所以

σ_X² = a

Quiz

Week7

7-1 期望值II

• 对连续的随机变数X而言，想求期望值，我们用类似 离散随机变数的方式出发
• 将X的值 以Δ为单位 无条件舍去来近似结果 离散随机变数 Y
  • 当 Δ → 0时， X≈Y , 当Δ趋近0的时候，Y接近Y
  • X∈[0,1Δ) -> Y=0Δ
  • X∈[1Δ,2Δ) -> Y=1Δ
  • X∈[nΔ,(n+1Δ) -> Y=nΔ
• 根据第五周
  • p_Y(nΔ) = P(nΔ ≤ X < nΔ+Δ) ≈ f_X(nΔ)·Δ
• E[X] = lim_Δ→0E[Y] = lim_Δ→0 ∑_n=-∞^∞ nΔ·P_Y(nΔ)
  • = ∫_-∞^∞ xf_X(x)dx
  • 即， x乘上pdf,然后积分
    • 一般来说, 求一个 函数 f(x) 在 x∈ [a,b] 之间的均值, 一般是 求出原函数F, 均值就是 (F(b)-F(a))/(b-a)
    • pdf 本身就蕴含一点均值的计算，求期望值只需要计算 F(b)-F(a) ?

随机变数函数 期望值

• 对于任一连续随机变数X，其任意函数g(X)亦是一随机变数
  • E[g(X)] = ∫_-∞^∞ g(x)f_X(x)dx

常见连续分布的期望值/变异数

• X ~ Exponential(λ)
  • μ = 1/λ
  • σ² = 1/λ²
• X ~ Erlang(n,λ)
  • μ = n/λ
  • σ² = n/λ²
• X ~ Gaussian(μ,σ)
  • μ = μ
  • σ² = σ²
• X ~ UNIF(a,b)
  • μ = (a+b)/2
  • σ² = 1/12 · (b-a)²

期望值推导

• 一些有用的微积分性质
  • e^*𝑑* = 𝑑e^*
  • ∫U𝑑V = UV - ∫VdU
  • ∫c𝑑x = ∫𝑑cx , c 是常数
  • ∫pdf = 1

7.2 隨機變數之函數

• 随机变数X的任意函数g(X)也是一个随机变数
• 通常被称为 Derived Random Variable
  • 从 random variable X 衍生出来的一个新的random variable

如何求 g(X)几率分布?

• 若X为离散
  • 直接推 g(X) 的 PMF

• 若X为连续

  • 先推 g(X)的CDF， 再微分得到PDF

• Ex:某宅宅超爱战LOL。每次一战就连续战 𝑿 场不可收拾，已知 𝑿~GEO(0.2)。某宅宅内心仍有 一点清明，其良心亦会因战过度而内疚，依战的次数 多寡，内疚程度 𝒀分别为1, 2, 3 不同等级:

               ⎧ 1, if 1≤X≤3
    Y = g(X) = ⎨ 2, if 4≤X≤6
               ⎩ 3, if X≥7
  

  • 问Y=g(X)的几率分布?
  • 解: X~GEO(0.2) => p_X(x) = (1-0.2)^x-1·0.2
    • p_Y(1) = p_X(1)+p_X(2)+p_X(3)
      • = 0.2 + 0.8·0.2 + 0.8²·0.2
    • p_Y(2) = p_X(4)+p_X(5)+p_X(6)
      • = (0.8)³·0.2 + (0.8)⁴·0.2 + (0.8)⁵·0.2
    • p_Y(3) = P(Y=3) = 1-p_Y(2)-p_Y(3)
• 离散g(X)
  • Y = g(X) 的 PMF为
  • 
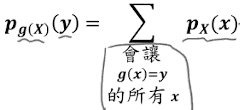
• 连续g(X)
  • 先计算g(X)的CDF:
    • F_g(X)(y) = P[g(X)≤y]
  • 若 g(X)可微分, 再对y微分得到PDF:
    • 

• 连续g(x) = aX + b

  • Ex1: 若Y=3X+2, 请问Y的PDF 跟f_X(x)之关系为何?
  • F_Y(y) = P(Y≤y)
    • = P(3X+2≤y)
    • = P(X≤(y-2)/3 )
    • = F_X( (y-2)/3 )
  • f_Y(y) = f_X( (y-2)/3 )·(1/3)

  • generic solution:

    • f_Y(y) = (1/|a|)·f_X( (y-b)/a )

  • Ex2: X~Exponential(λ) , Y = 2X

  • f_X(x) = λe^-λxu(x), Y=2x (a=2,b=0)
    • 这里 u(x)是工程上常见的一个函数，表示只有x>0时有值，即x>0时u(x)=1, 其他情况u(x)=0
  • f_Y(y) = (1/|a|)·f_X( (y-b)/a )
    • = 1/2·λe^-λ·y/2·u(y/2) (a,b代入)
    • = λ/2·e^-λ/2·y·u(y)
    • => Y~Exponential(λ/2)
• 连续g(x) = aX² + b
  • Ex: Y = 2X²+1, X~UNIF(-1,7), 求 Y的PDF
  • 不要好高骛远，先算CDF
  • F_Y(y) = P(Y=2X²+1≤y)
    • = P(X²≤(y-1)/2)
    • = P( -√((y-1)/2) ≤ X ≤ √((y-1)/2) )
    • = ∫_-z^zf_X(x)dx , 令 z = √((y-1)/2)
  • 需要注意积分的范围, 这里注意 Y > 3的情况
    • y≤3: F_Y(y) = ∫_-z^z1/8dx =
    • y>3: F_Y(y) = ∫_-1^z1/8dx =
    • 微分得到 f_Y(y)

7.3a 条件概率分布

• Ex:为了更了解宅宅的心，店员妹亦开始战 LOL。 已知店员妹战LOL场数 𝑿~UNIF (1, 5)。若已知 店员妹战了两场仍战意甚浓、继续战。请问在此情况下，店员妹 今日战LOL场数 𝑿 之机率分布为何?
  • 条件 B: 已战两场 仍想战
  • p_X|B(x) = P(X=x|B) = P(X=x,B)/P(B)
    • = (1/5) / (3/5) = 1/3, x∈B:x=3,4,5
    • = 0, x∉B:x=otherwise
• 若𝑿是一离散随机变数，其PMF为 𝒑𝑿(𝒙)。若已知某事件 𝑩 已发生，则在此情况下 之条件机率分布为:
  • 
• Ex:店员妹等公交车上班。通常等公交车的时间 𝑿， 从零到十分钟间可能性均等。若店员妹已等了 五分钟车还没来。请问在此情况下，等车时间 𝑿 之机率分布为何?
  • B: X>5 => P(B)=0.5
  • f_X|B = x∈B: f_X(x) / P(B)
    • = x∉B: 0
• 若𝑿是一连续随机变量，其PDF为 𝒇𝑿(𝒙)。若已知某事件 𝑩 已发生，则在此情况下 之条件机率分布为:
  • 
• 条件期望值 Conditional Expectation
  • 
  • 

7.3a 失忆性 (Memoryless)

• 宅宅与店员妹相约出门。宅宅出门前在战LOL，场数 𝑿~GEO (𝟎.2) 。店员妹等了两场后，宅宅还在玩。 店员妹甚怒，怒催宅宅。宅宅曰「快好了、快好了」。问宅宅剩余场 数 𝑿’ 之机率分布为何?

• 店员妹与宅宅相约出门。店员妹出门前化妆时间为 𝑿(小时)， 𝑿~Exponential(𝟏)。经过一小时后， 仍未完成。宅宅甚怒，怒催店员妹。店员妹曰「快好了、快好了」。 问店员妹剩余化妆时间𝑿′机率分布为何?

• Geometric 跟 Exponential 机率分布 皆有失忆性的性质

  • 不管事情已经进行多久，对于事情之后的进行 一点影响都没有!

QUIZ