Java 程序:确定给定矩阵是否为稀疏矩阵
在本教程中,我们将学习如何确定给定的矩阵是否是稀疏矩阵。如果一个矩阵的大部分元素都是 0,那么这个矩阵就是稀疏矩阵。但是在继续之前,如果您不熟悉数组的概念,那么请务必查看 Java 中的文章数组。
下面是同样的图示。
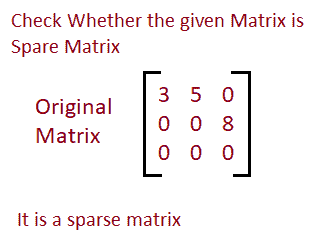
输入:输入矩阵元素:
1 4 0
0 0 0
4 0 0
输出:是稀疏矩阵。
程序 1:确定给定的矩阵是否是稀疏矩阵
在这个程序中,我们将学习当值是用户定义的时,如何确定给定的矩阵是否是稀疏矩阵。在这里,我们将要求用户输入值,然后,我们将检查给定的矩阵是否是稀疏矩阵。
算法
- 开始
- 声明变量来存储矩阵的大小。
- 要求用户初始化行数和列数。
- 声明一个矩阵。
- 要求用户初始化矩阵的元素。
- 打印原始矩阵
- 声明一个变量来存储矩阵的大小。
- 声明一个变量来计算矩阵中 0 个元素的数量。
- 使用循环计算所有的零元素。
- 如果发现任何 0 元素,则增加计数。
- 检查计数是否大于大小的一半。
- 如果更大,则将其打印为稀疏矩阵。
- 否则打印它不是稀疏矩阵。
- 停下来。
下面是相同的代码。
//Java Program to check whether the given matrix is sparse or not*/
import java.util.Scanner;
public class Main
{
public static void main(String[] args)
{
// declare variables
int m, n;
// To take input from the user
Scanner sc = new Scanner(System.in);
System.out.println("Enter the number of rows ");
// Initialize the number of rows
m = sc.nextInt();
System.out.println("Enter the number of columns ");
// Initialize the number of columns
n = sc.nextInt();
// declare a mxn order array
int a[][] = new int[m][n];
System.out.println("Enter all the values of matrix ");
// Initialize the matrix elements
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
a[i][j] = sc.nextInt();
}
}
System.out.println("Original Matrix:");
// print the original matrix
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
System.out.print(a[i][j] + " ");
}
System.out.println("");
}
int size= m*n; //Stores the size of the matrix
int count=0; //Variable to check for the number of 0 elements
//Loop to count all zero element present in matrix
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(a[i][j] == 0) //Check if element is 0 or not
count++; //Increment the count if 0 element is found
}
}
if(count>(size/2))
System.out.println("It is a sparse matrix");
else
System.out.println("It is not a sparse matrix");
}
}
输入行数 3 输入列数 3 输入矩阵 1 的所有值 2 0 0 0 0 0 0 原始矩阵: 1 2 0 0 0 0 0 0 0 它是一个稀疏矩阵
程序 2:确定给定的矩阵是否是稀疏矩阵
在这个程序中,我们将学习当值被预定义时,如何确定给定的矩阵是否是稀疏矩阵。这里,矩阵的元素是在程序中预先定义的。因此,基于该矩阵的值,我们将检查给定的矩阵是否是稀疏矩阵。
算法
- 开始
- 声明并初始化矩阵。
- 声明变量来存储矩阵的行数和列数。
- 打印原始矩阵。
- 声明一个变量来存储矩阵的大小。
- 声明一个变量来计算矩阵中 0 个元素的数量。
- 使用循环计算所有的零元素。
- 如果发现任何 0 元素,则增加计数。
- 检查计数是否大于大小的一半。
- 如果更大,则将其打印为稀疏矩阵。
- 否则打印它不是稀疏矩阵。
- 停下来。
下面是相同的代码。
//Java Program to check whether the given matrix is sparse or not*/
public class Main
{
public static void main(String[] args)
{
// declare and initialize a matrix
int a[][] = {{ 2, 9, 8 }, { 7, 6, 4 }, { 3, 9, 2 } };
int m=a.length; //Stores the number of rows in a matrix
int n=a[0].length; //Stores the number of columns in a matrix
// print the original matrix
System.out.println("Original Matrix:");
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
System.out.print(a[i][j] + " ");
}
System.out.println("");
}
int size= m*n; //Stores the size of the matrix
int count=0; //Variable to check for the number of 0 elements
//Loop to count all zero element present in matrix
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(a[i][j] == 0) //Check if element is 0 or not
count++; //Increment the count if 0 element is found }
}
if(count>(size/2))
System.out.println("It is a sparse matrix");
else
System.out.println("It is not a sparse matrix");
}
}
原始矩阵: 2 9 8 7 6 4 3 9 2 它不是稀疏矩阵