二分查找插入点

二分查找不仅可用于搜索目标元素，还可用于解决许多变种问题，比如搜索目标元素的插入位置。

无重复元素的情况

!!! question

给定一个长度为 $n$ 的有序数组 `nums` 和一个元素 `target` ，数组不存在重复元素。现将 `target` 插入数组 `nums` 中，并保持其有序性。若数组中已存在元素 `target` ，则插入到其左方。请返回插入后 `target` 在数组中的索引。示例如下图所示。

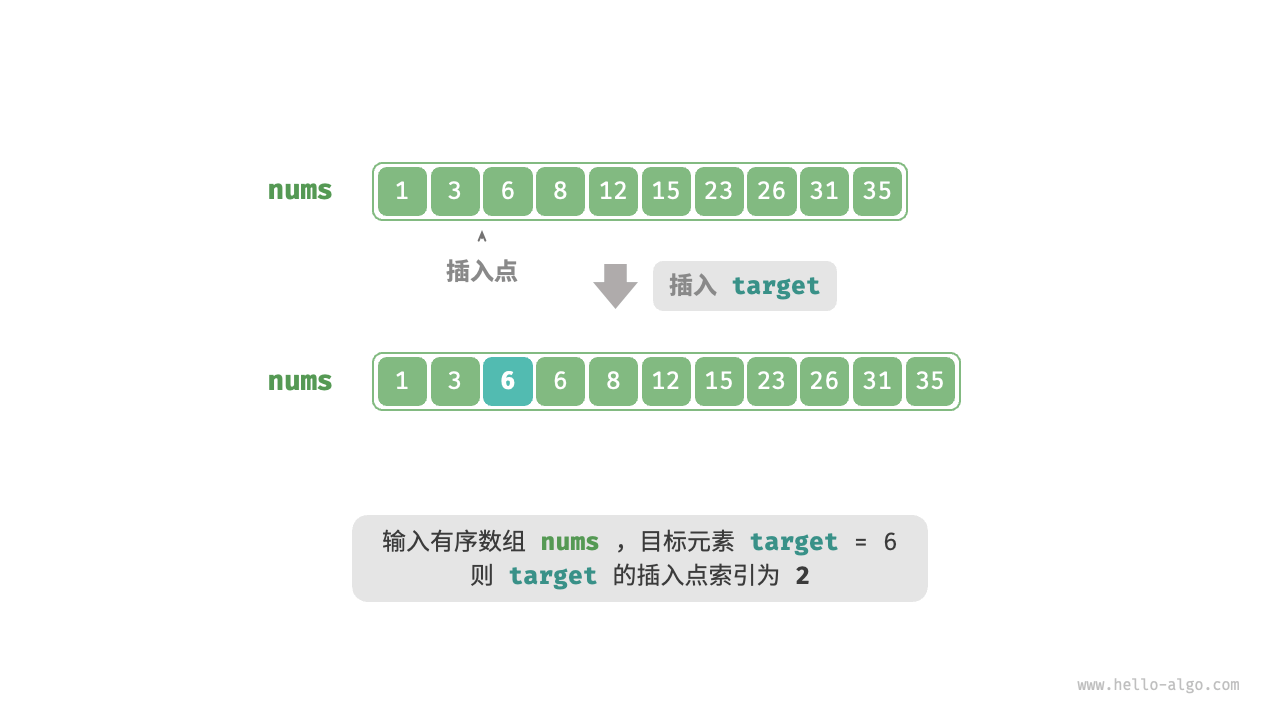
如果想复用上一节的二分查找代码，则需要回答以下两个问题。

问题一：当数组中包含 target 时，插入点的索引是否是该元素的索引？

题目要求将 target 插入到相等元素的左边，这意味着新插入的 target 替换了原来 target 的位置。也就是说，当数组包含 target 时，插入点的索引就是该 target 的索引。

问题二：当数组中不存在 target 时，插入点是哪个元素的索引？

进一步思考二分查找过程：当 nums[m] < target 时 $i$ 移动，这意味着指针 $i$ 在向大于等于 target 的元素靠近。同理，指针 $j$ 始终在向小于等于 target 的元素靠近。

因此二分结束时一定有：$i$ 指向首个大于 target 的元素，$j$ 指向首个小于 target 的元素。易得当数组不包含 target 时，插入索引为 $i$ 。代码如下所示：

• "Python"

  def binary_search_insertion_simple(nums: list[int], target: int) -> int:
    """二分查找插入点（无重复元素）"""
    i, j = 0, len(nums) - 1 // 初始化双闭区间 [0, n-1]
    while i <= j:
        m = (i + j) // 2 // 计算中点索引 m
        if nums[m] < target:
            i = m + 1 // target 在区间 [m+1, j] 中
        elif nums[m] > target:
            j = m - 1 // target 在区间 [i, m-1] 中
        else:
            return m // 找到 target ，返回插入点 m
   // 未找到 target ，返回插入点 i
    return i
  

• "C++"

  /* 二分查找插入点（无重复元素） */
  int binarySearchInsertionSimple(vector<int> &nums, int target) {
    int i = 0, j = nums.size() - 1; // 初始化双闭区间 [0, n-1]
    while (i <= j) {
        int m = i + (j - i) / 2; // 计算中点索引 m
        if (nums[m] < target) {
            i = m + 1; // target 在区间 [m+1, j] 中
        } else if (nums[m] > target) {
            j = m - 1; // target 在区间 [i, m-1] 中
        } else {
            return m; // 找到 target ，返回插入点 m
        }
    }
    // 未找到 target ，返回插入点 i
    return i;
  }
  

• "Java"

  /* 二分查找插入点（无重复元素） */
  int binarySearchInsertionSimple(int[] nums, int target) {
    int i = 0, j = nums.length - 1; // 初始化双闭区间 [0, n-1]
    while (i <= j) {
        int m = i + (j - i) / 2; // 计算中点索引 m
        if (nums[m] < target) {
            i = m + 1; // target 在区间 [m+1, j] 中
        } else if (nums[m] > target) {
            j = m - 1; // target 在区间 [i, m-1] 中
        } else {
            return m; // 找到 target ，返回插入点 m
        }
    }
    // 未找到 target ，返回插入点 i
    return i;
  }
  

存在重复元素的情况

!!! question

在上一题的基础上，规定数组可能包含重复元素，其余不变。

假设数组中存在多个 target ，则普通二分查找只能返回其中一个 target 的索引，而无法确定该元素的左边和右边还有多少 target。

题目要求将目标元素插入到最左边，所以我们需要查找数组中最左一个 target 的索引。初步考虑通过下图所示的步骤实现。

1. 执行二分查找，得到任意一个 target 的索引，记为 $k$ 。
2. 从索引 $k$ 开始，向左进行线性遍历，当找到最左边的 target 时返回。

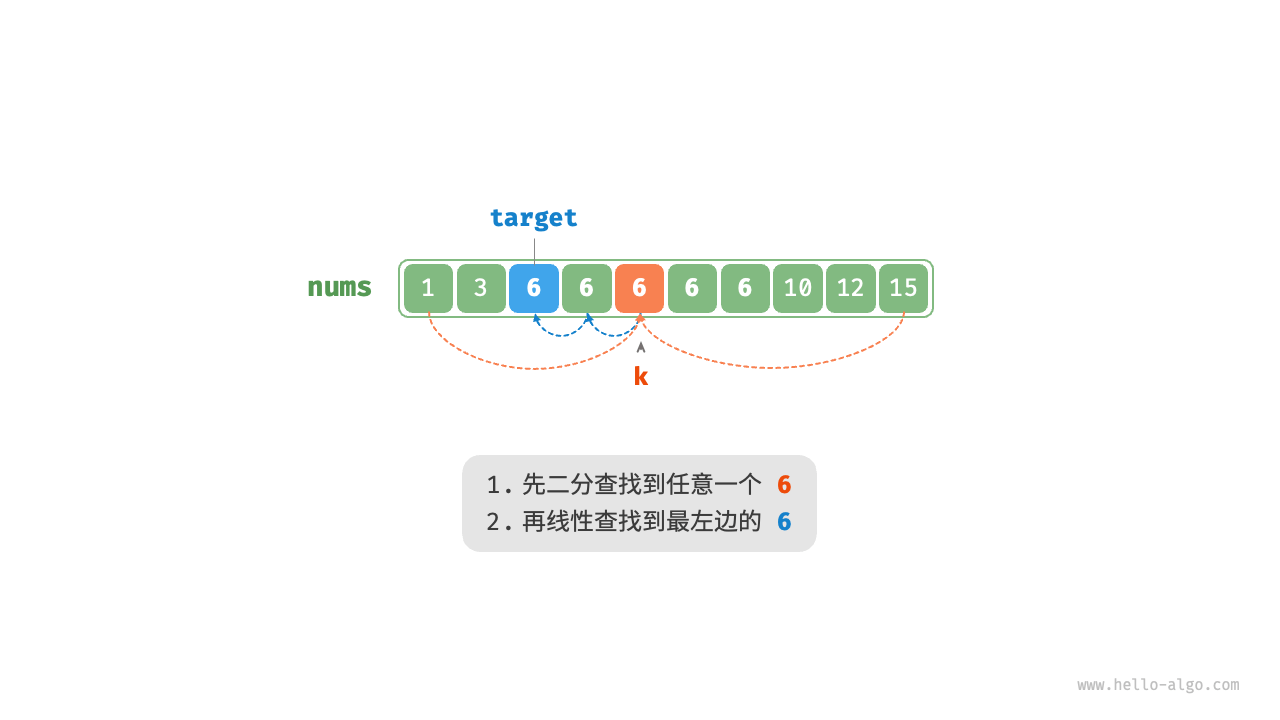
此方法虽然可用，但其包含线性查找，因此时间复杂度为 $O(n)$ 。当数组中存在很多重复的 target 时，该方法效率很低。

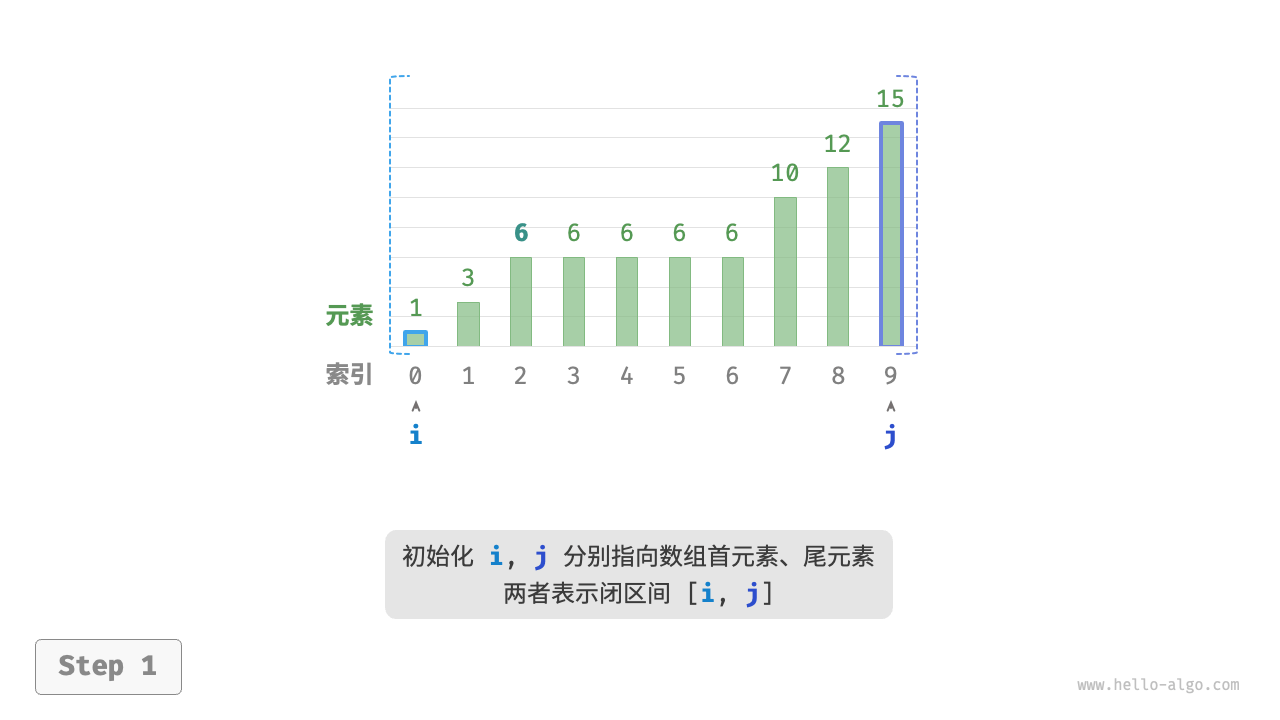
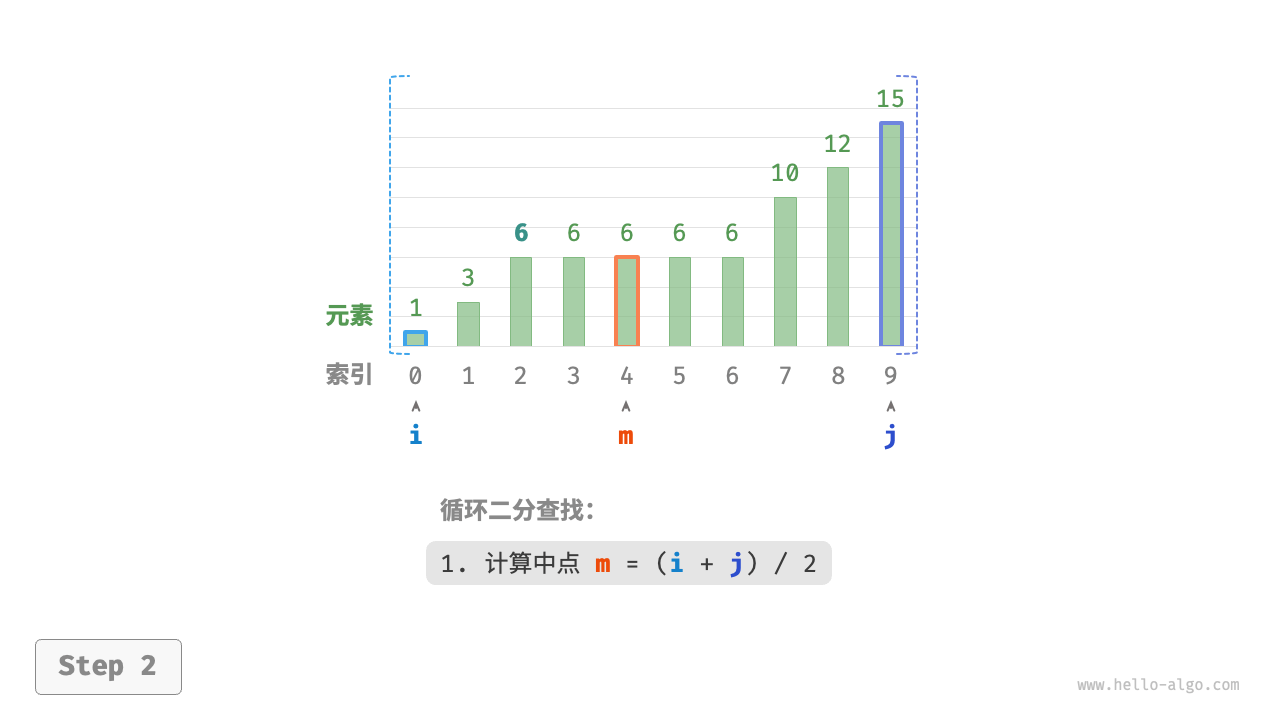
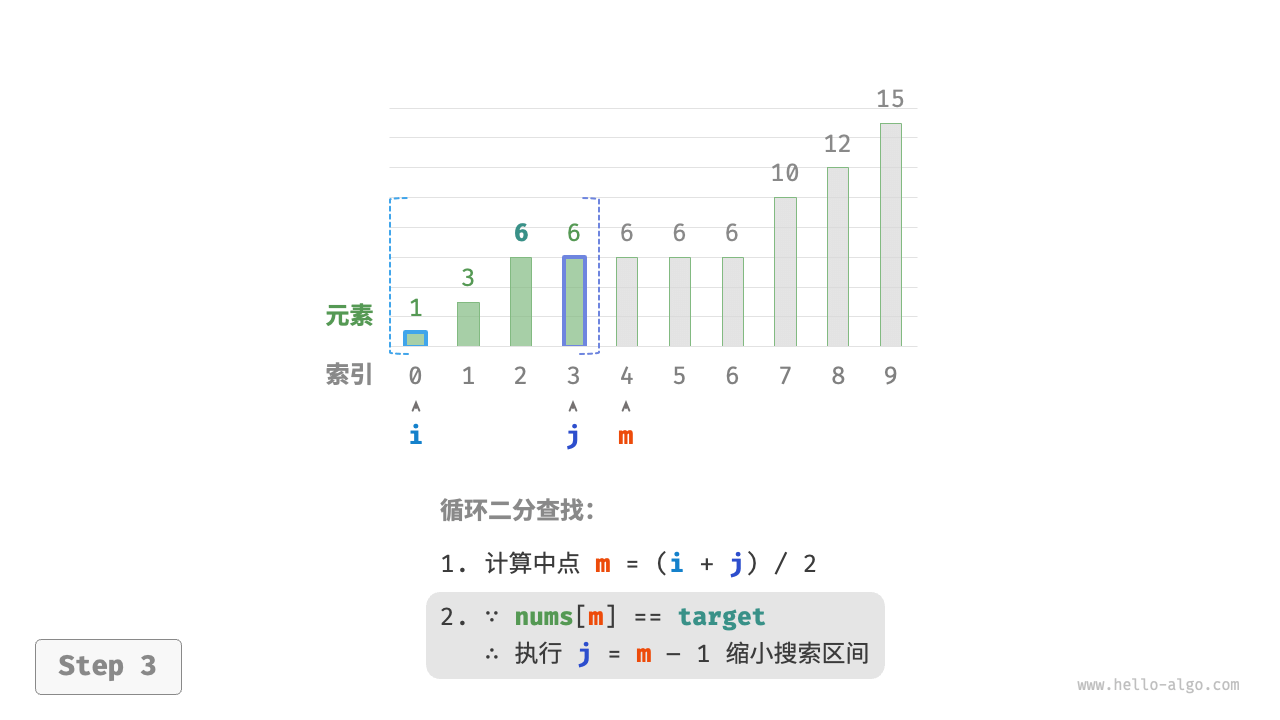
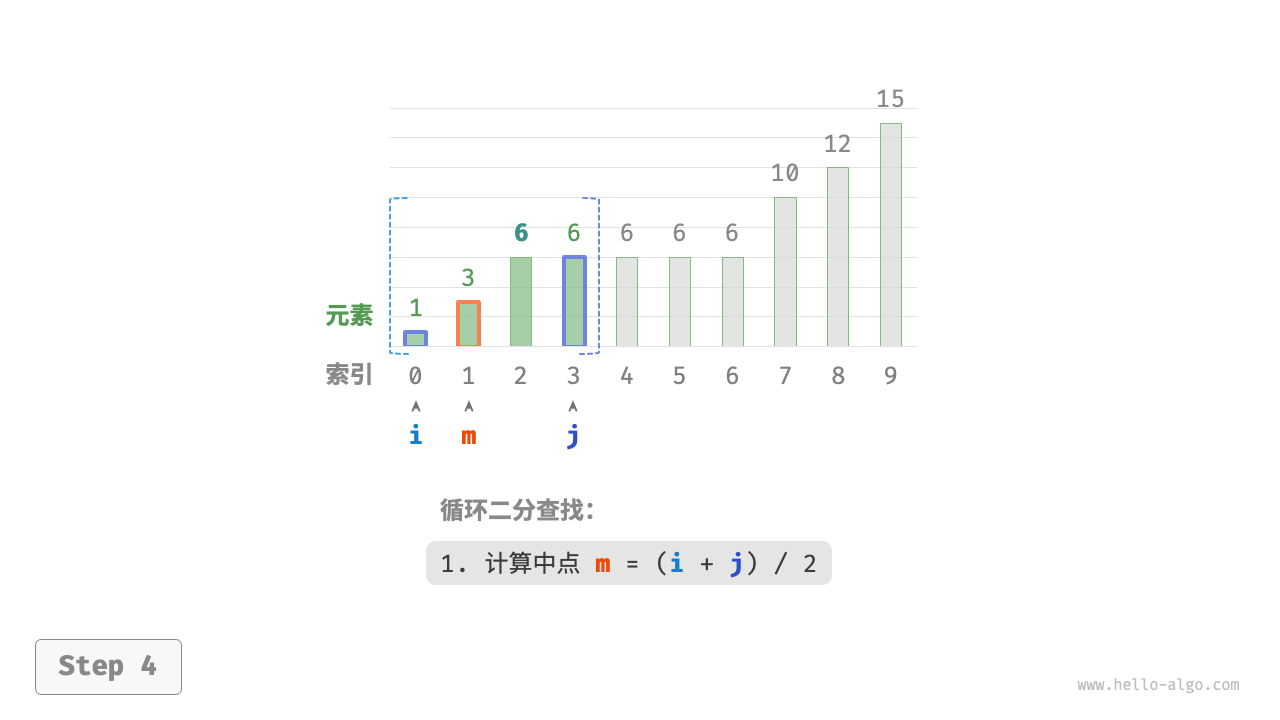
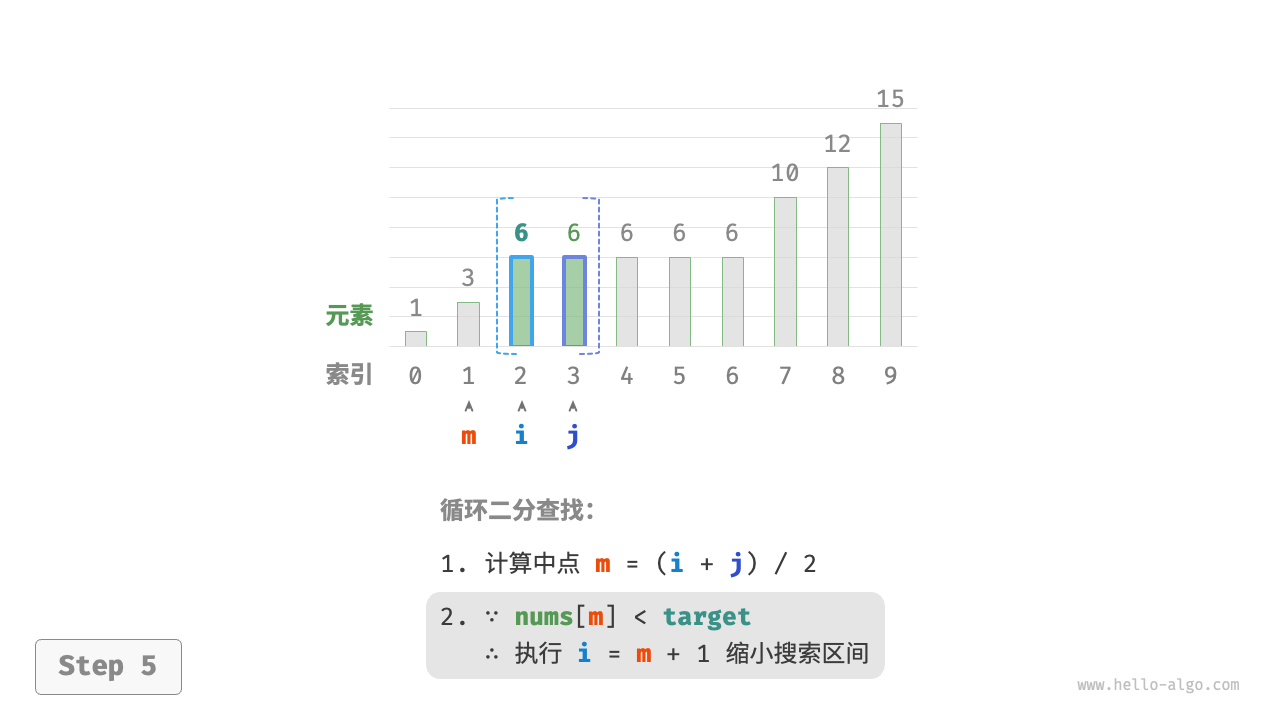
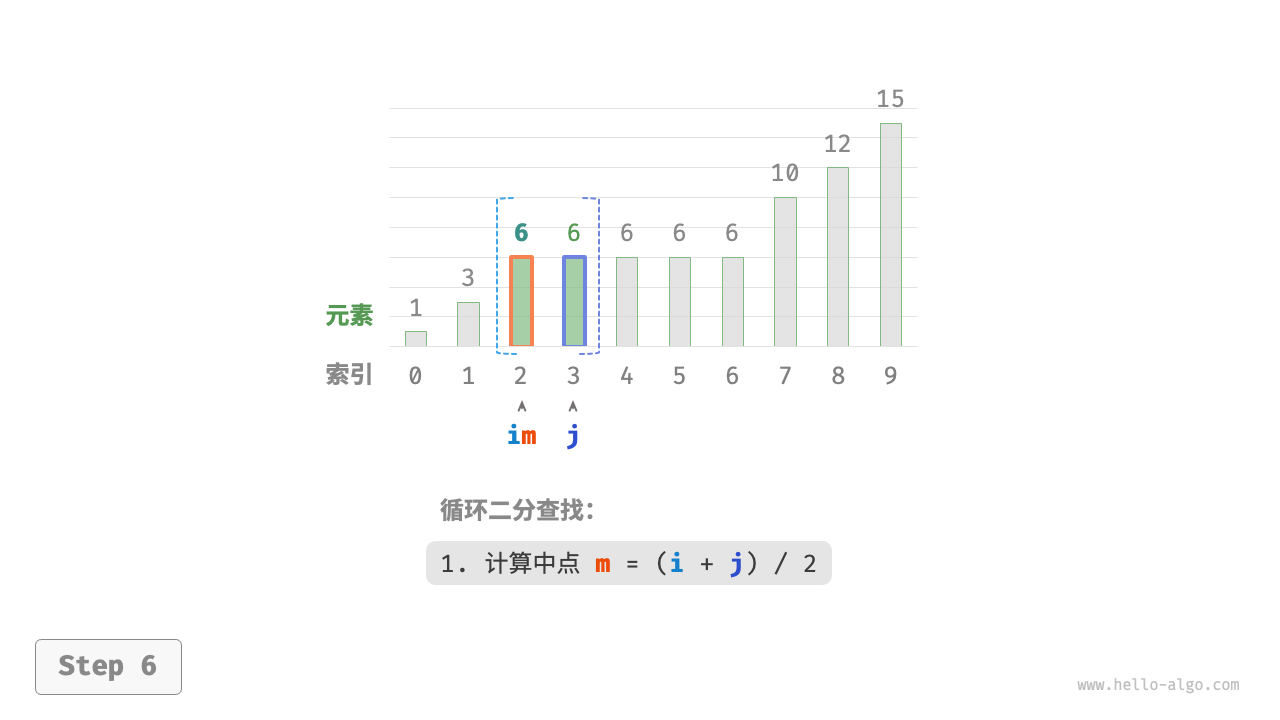
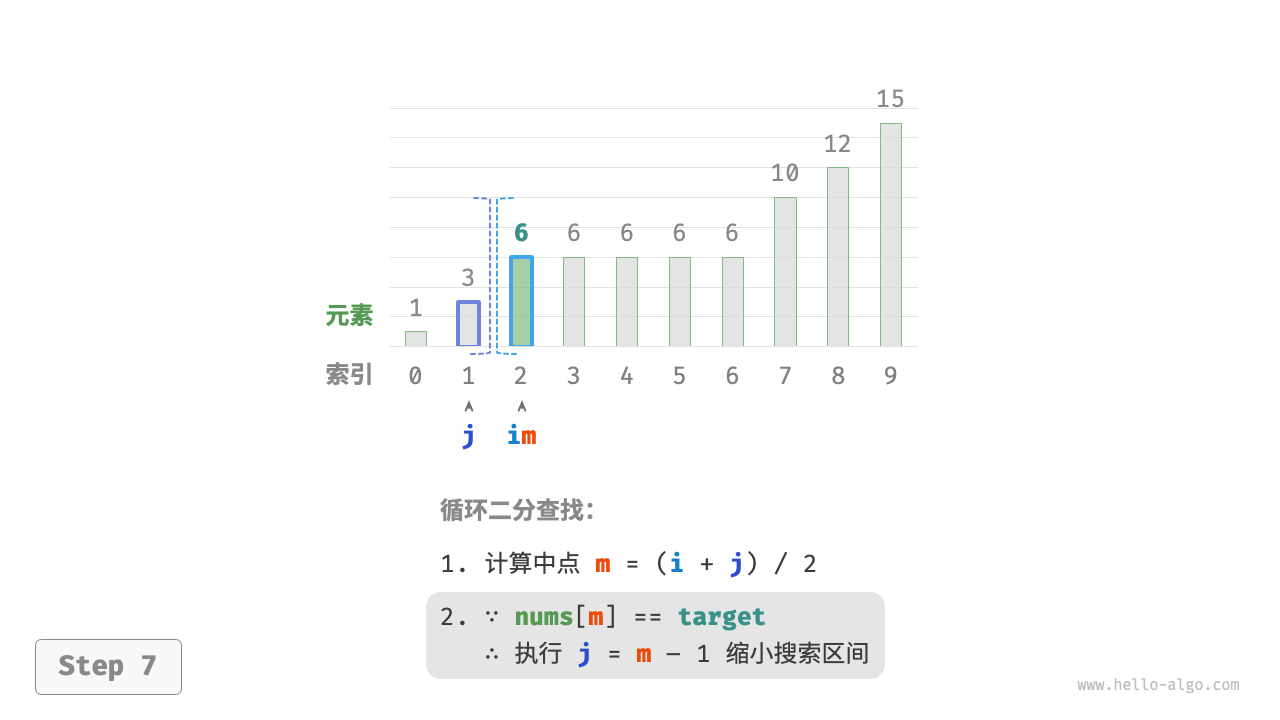
现考虑拓展二分查找代码。如下图所示，整体流程保持不变，每轮先计算中点索引 $m$ ，再判断 target 和 nums[m] 的大小关系，分为以下几种情况。

• 当 nums[m] < target 或 nums[m] > target 时，说明还没有找到 target ，因此采用普通二分查找的缩小区间操作，从而使指针 $i$ 和 $j$ 向 target 靠近。
• 当 nums[m] == target 时，说明小于 target 的元素在区间 $[i, m - 1]$ 中，因此采用 $j = m - 1$ 来缩小区间，从而使指针 $j$ 向小于 target 的元素靠近。

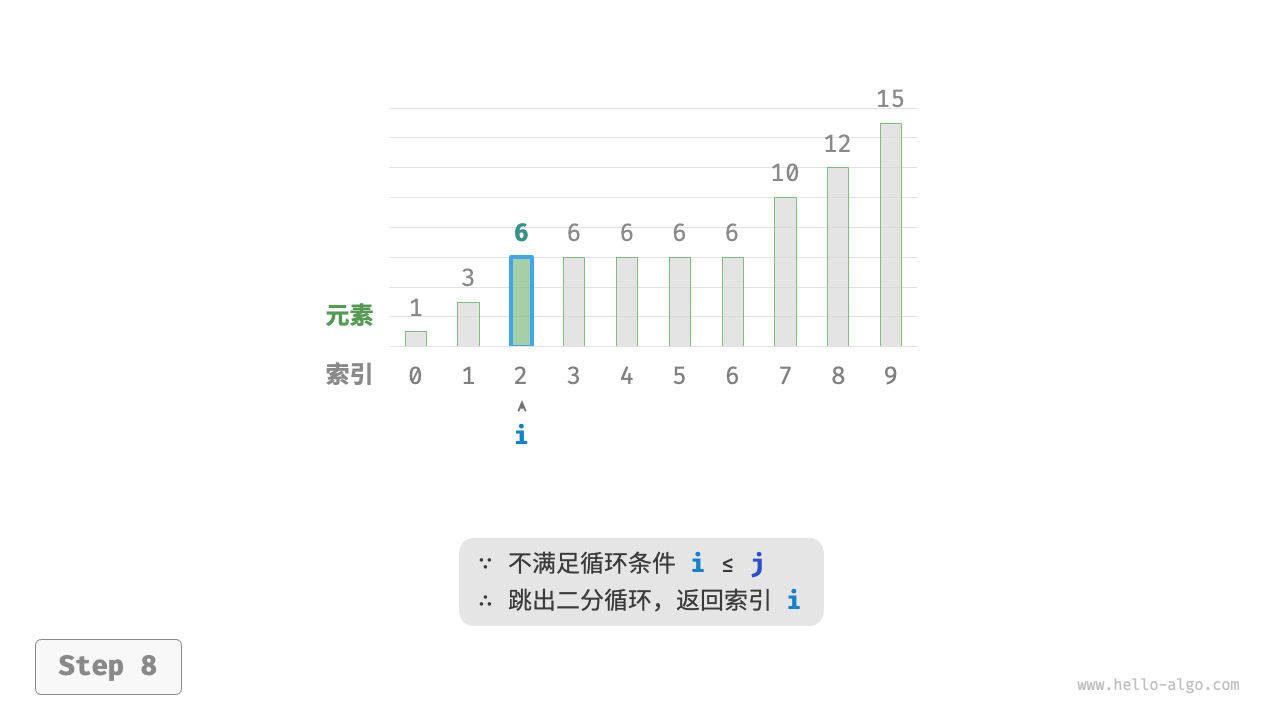
循环完成后，$i$ 指向最左边的 target ，$j$ 指向首个小于 target 的元素，因此索引 $i$ 就是插入点。

• "<1>"

• "<2>"

• "<3>"

• "<4>"

• "<5>"

• "<6>"

• "<7>"

• "<8>"

观察以下代码，判断分支 nums[m] > target 和 nums[m] == target 的操作相同，因此两者可以合并。

即便如此，我们仍然可以将判断条件保持展开，因为其逻辑更加清晰、可读性更好。

• "Python"

  def binary_search_insertion(nums: list[int], target: int) -> int:
    """二分查找插入点（存在重复元素）"""
    i, j = 0, len(nums) - 1 // 初始化双闭区间 [0, n-1]
    while i <= j:
        m = (i + j) // 2 // 计算中点索引 m
        if nums[m] < target:
            i = m + 1 // target 在区间 [m+1, j] 中
        elif nums[m] > target:
            j = m - 1 // target 在区间 [i, m-1] 中
        else:
            j = m - 1 // 首个小于 target 的元素在区间 [i, m-1] 中
   // 返回插入点 i
    return i
  

• "C++"

  /* 二分查找插入点（存在重复元素） */
  int binarySearchInsertion(vector<int> &nums, int target) {
    int i = 0, j = nums.size() - 1; // 初始化双闭区间 [0, n-1]
    while (i <= j) {
        int m = i + (j - i) / 2; // 计算中点索引 m
        if (nums[m] < target) {
            i = m + 1; // target 在区间 [m+1, j] 中
        } else if (nums[m] > target) {
            j = m - 1; // target 在区间 [i, m-1] 中
        } else {
            j = m - 1; // 首个小于 target 的元素在区间 [i, m-1] 中
        }
    }
    // 返回插入点 i
    return i;
  }
  

• "Java"

  /* 二分查找插入点（存在重复元素） */
  int binarySearchInsertion(int[] nums, int target) {
    int i = 0, j = nums.length - 1; // 初始化双闭区间 [0, n-1]
    while (i <= j) {
        int m = i + (j - i) / 2; // 计算中点索引 m
        if (nums[m] < target) {
            i = m + 1; // target 在区间 [m+1, j] 中
        } else if (nums[m] > target) {
            j = m - 1; // target 在区间 [i, m-1] 中
        } else {
            j = m - 1; // 首个小于 target 的元素在区间 [i, m-1] 中
        }
    }
    // 返回插入点 i
    return i;
  }
  

!!! tip

本节的代码都是“双闭区间”写法。有兴趣的读者可以自行实现“左闭右开”写法。

总的来看，二分查找无非就是给指针 $i$ 和 $j$ 分别设定搜索目标，目标可能是一个具体的元素（例如 target ），也可能是一个元素范围（例如小于 target 的元素）。

在不断的循环二分中，指针 $i$ 和 $j$ 都逐渐逼近预先设定的目标。最终，它们或是成功找到答案，或是越过边界后停止。