堆排序

!!! tip

阅读本节前，请确保已学完“堆“章节。

「堆排序 heap sort」是一种基于堆数据结构实现的高效排序算法。我们可以利用已经学过的“建堆操作”和“元素出堆操作”实现堆排序。

1. 输入数组并建立小顶堆，此时最小元素位于堆顶。
2. 不断执行出堆操作，依次记录出堆元素，即可得到从小到大排序的序列。

以上方法虽然可行，但需要借助一个额外数组来保存弹出的元素，比较浪费空间。在实际中，我们通常使用一种更加优雅的实现方式。

算法流程

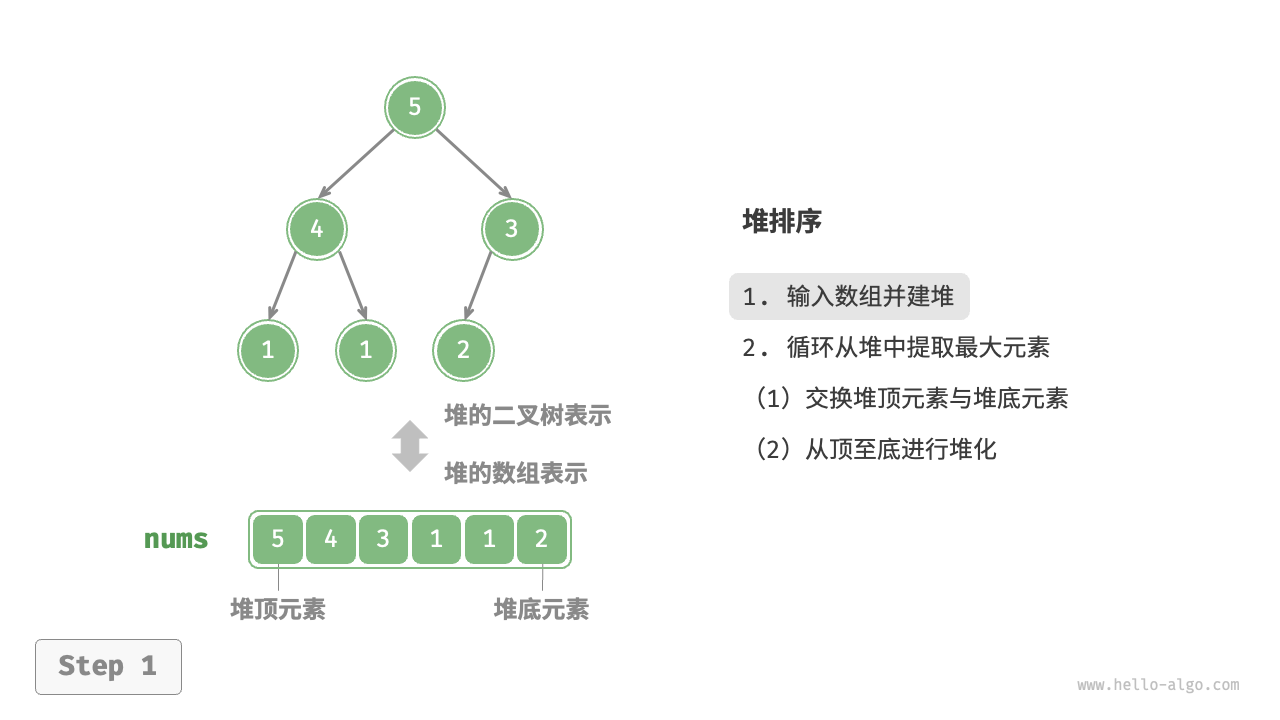
设数组的长度为 $n$ ，堆排序的流程如下图所示。

1. 输入数组并建立大顶堆。完成后，最大元素位于堆顶。
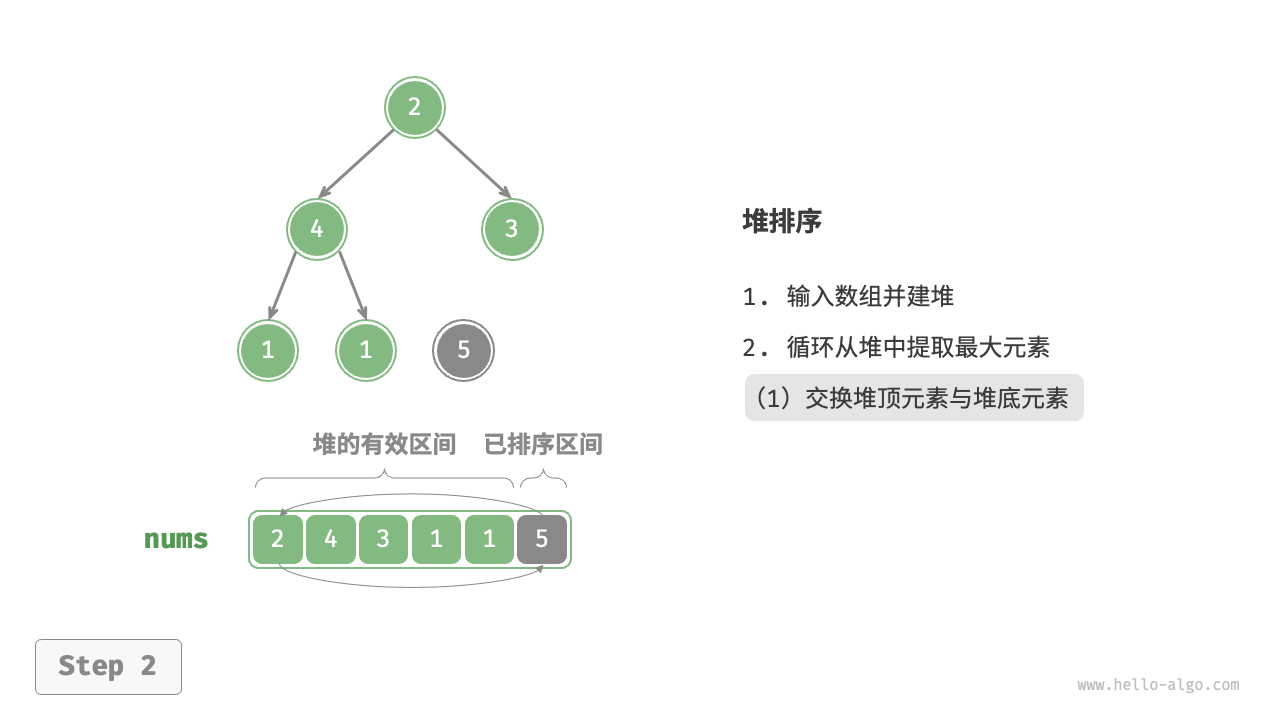
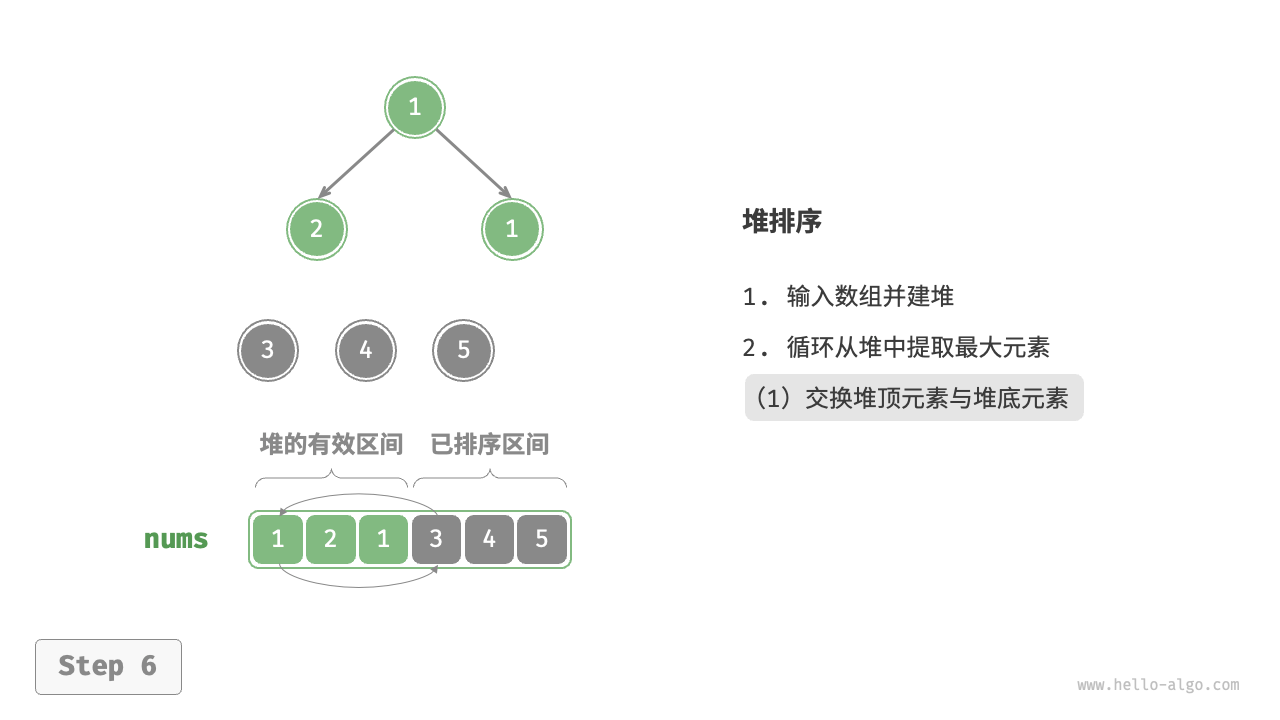
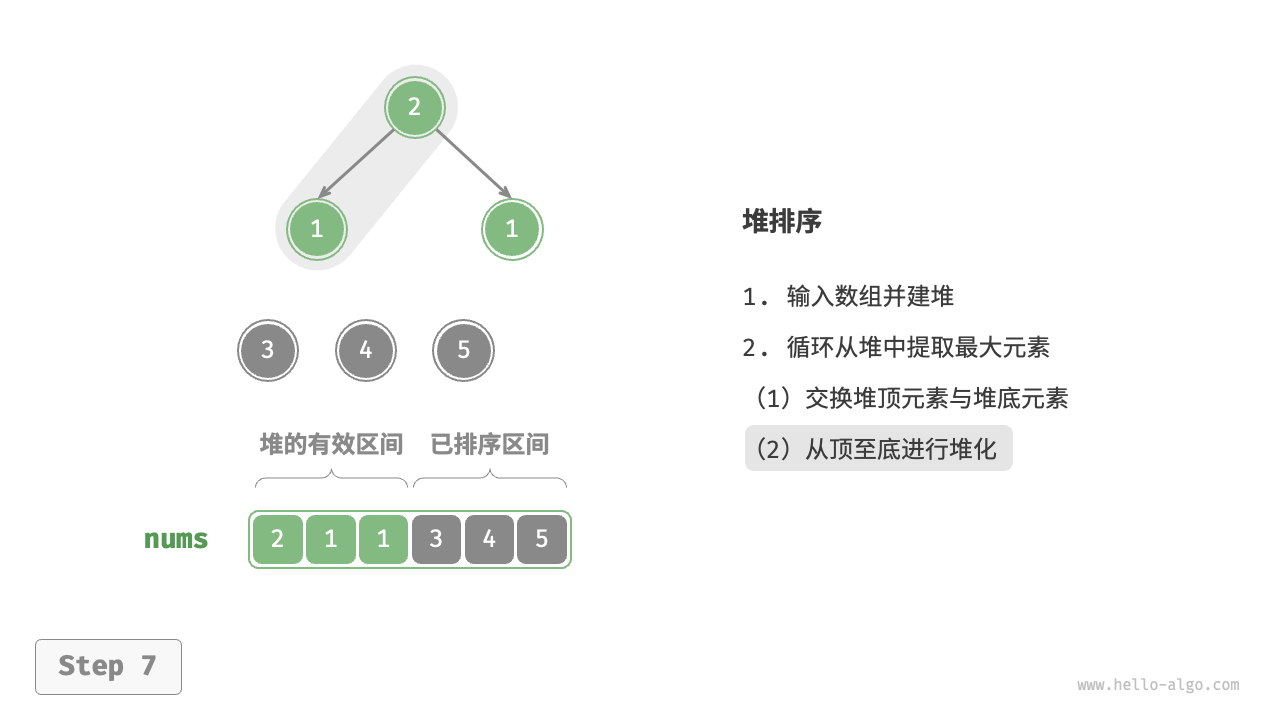
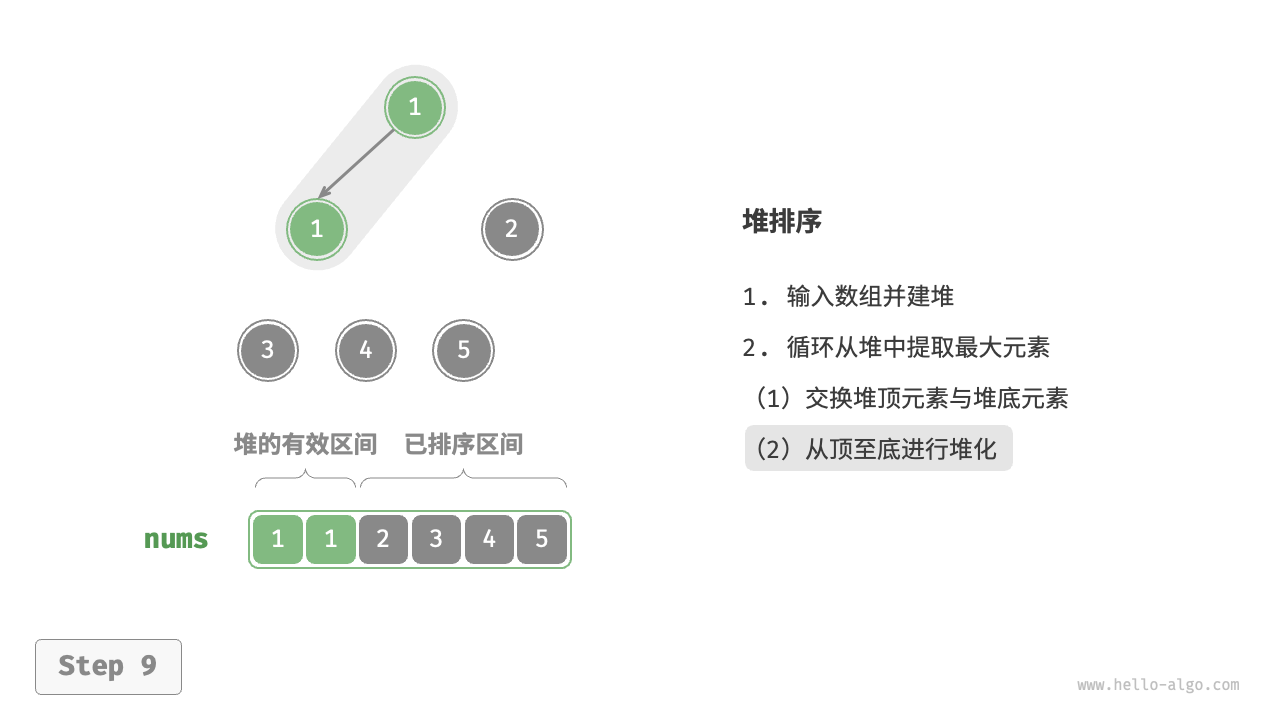
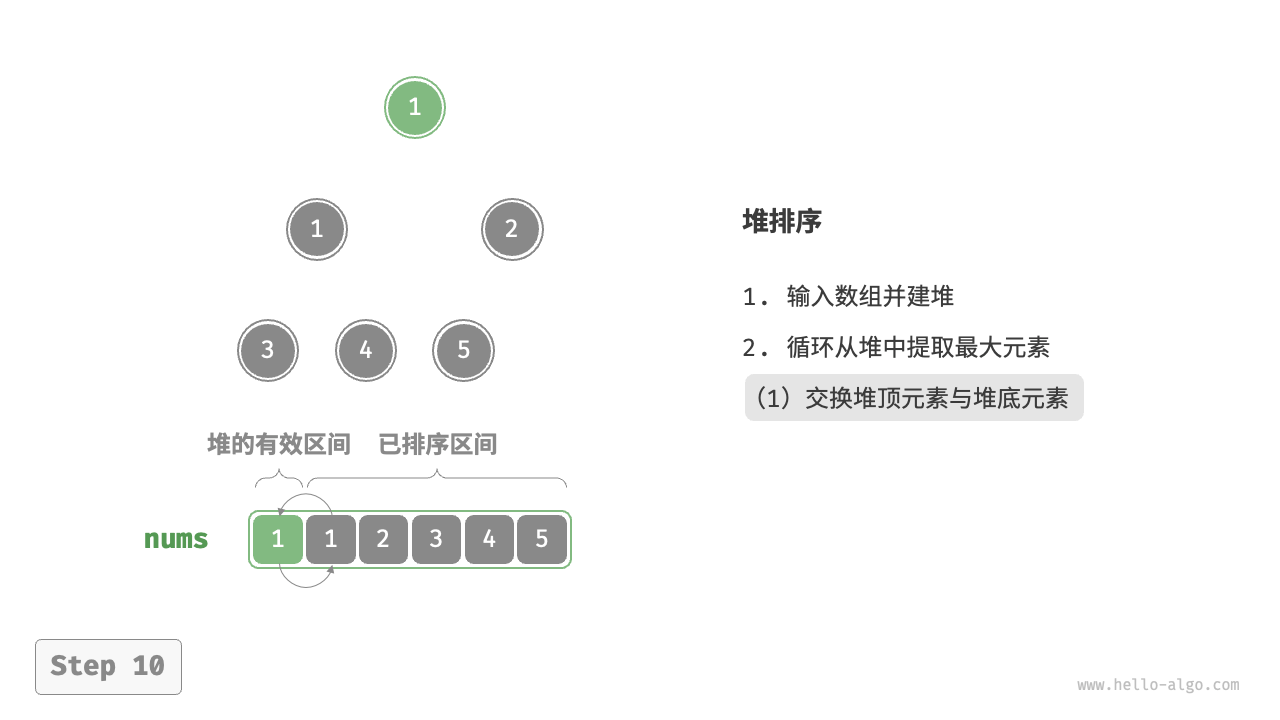
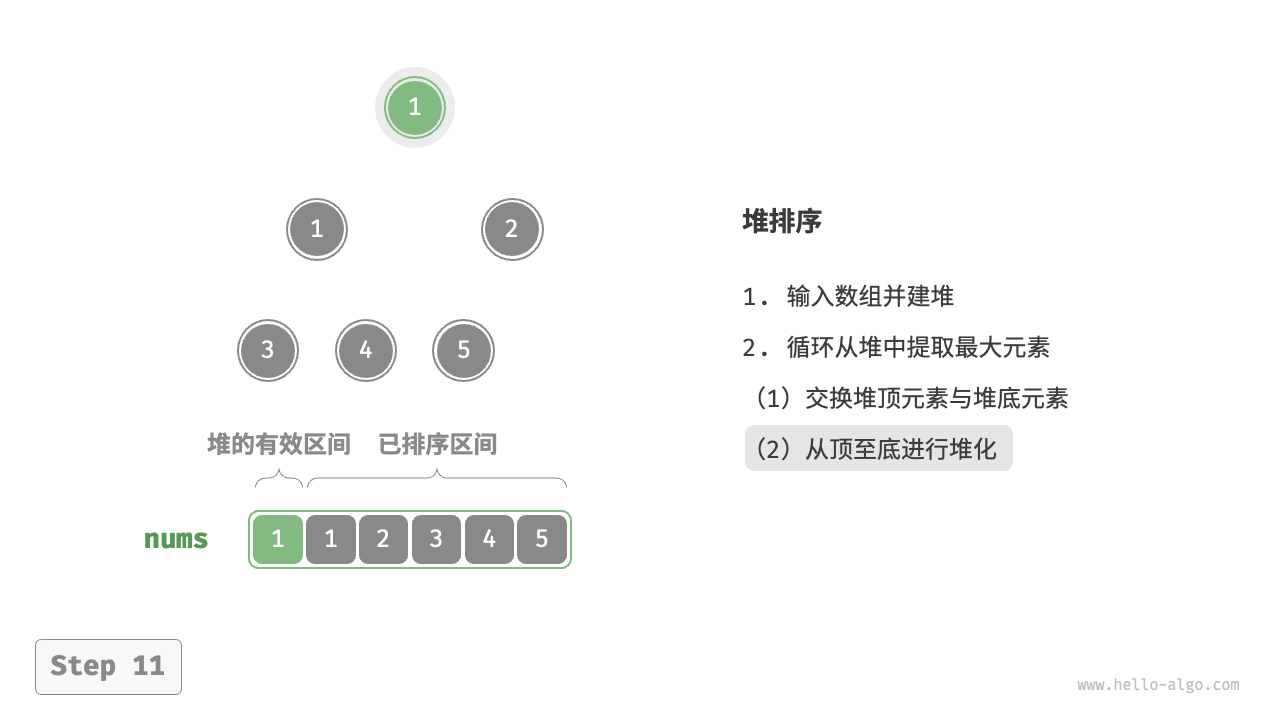
2. 将堆顶元素（第一个元素）与堆底元素（最后一个元素）交换。完成交换后，堆的长度减 $1$ ，已排序元素数量加 $1$ 。
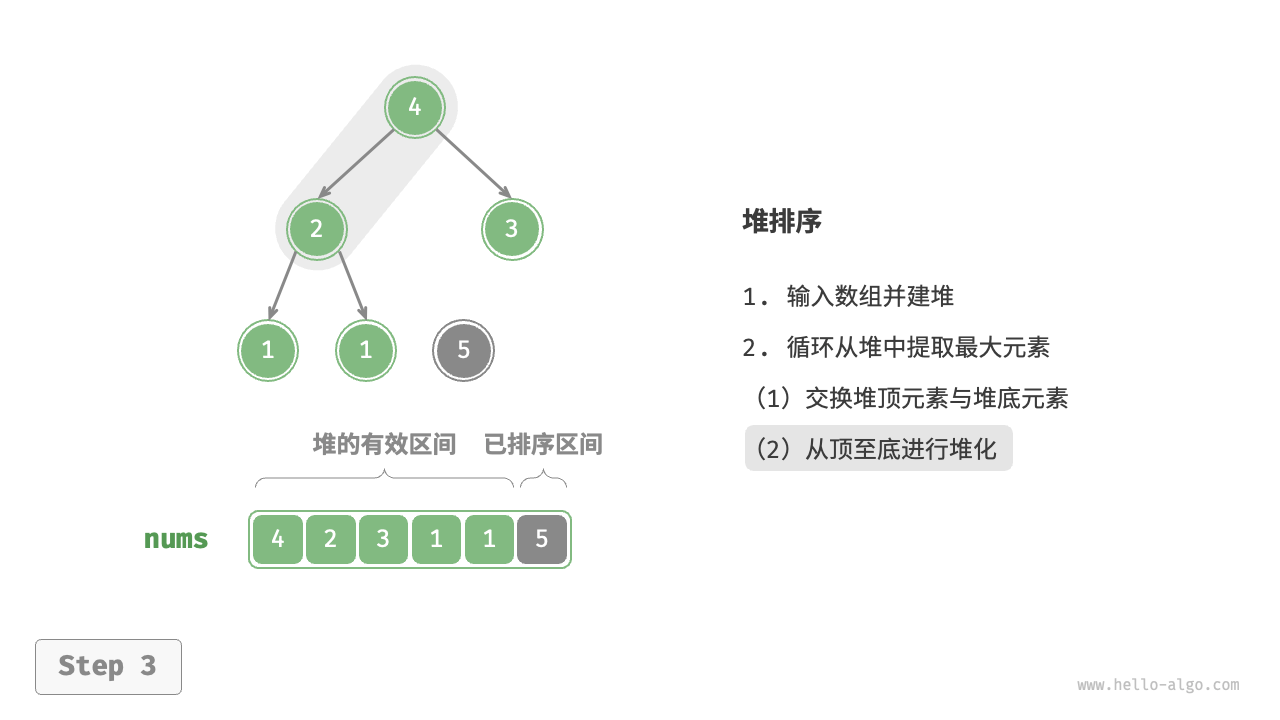
3. 从堆顶元素开始，从顶到底执行堆化操作（Sift Down）。完成堆化后，堆的性质得到修复。
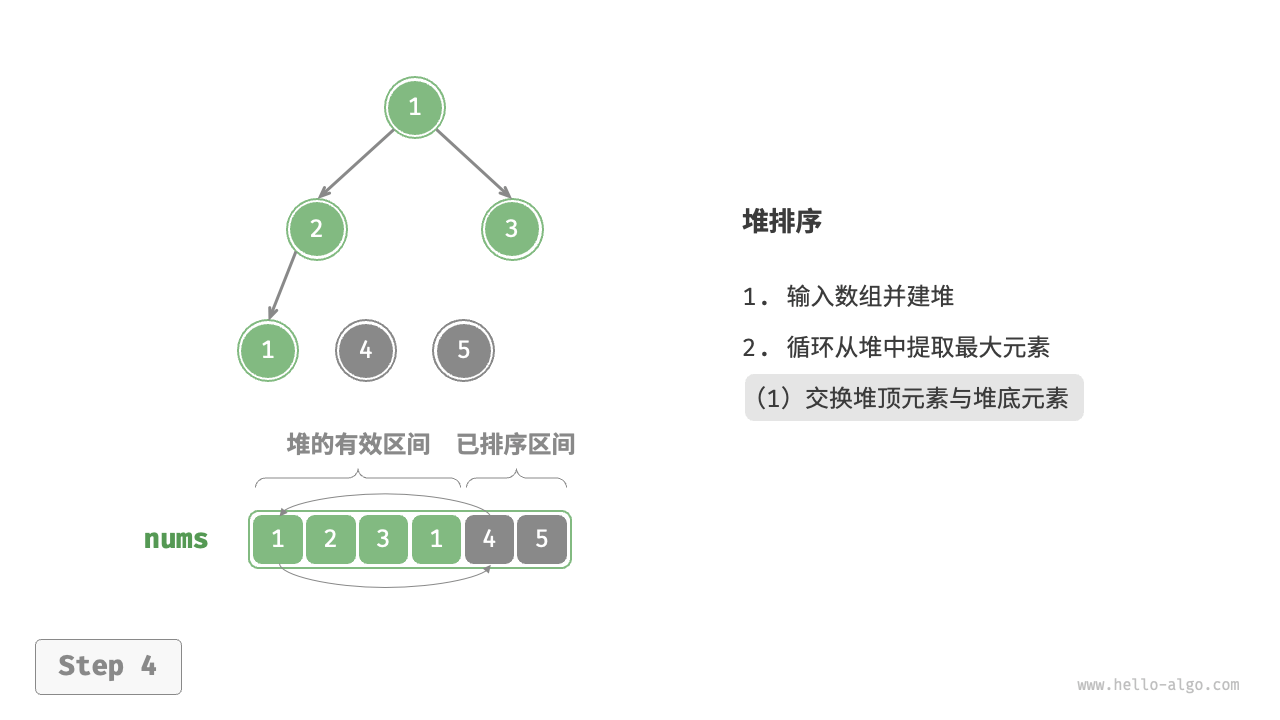
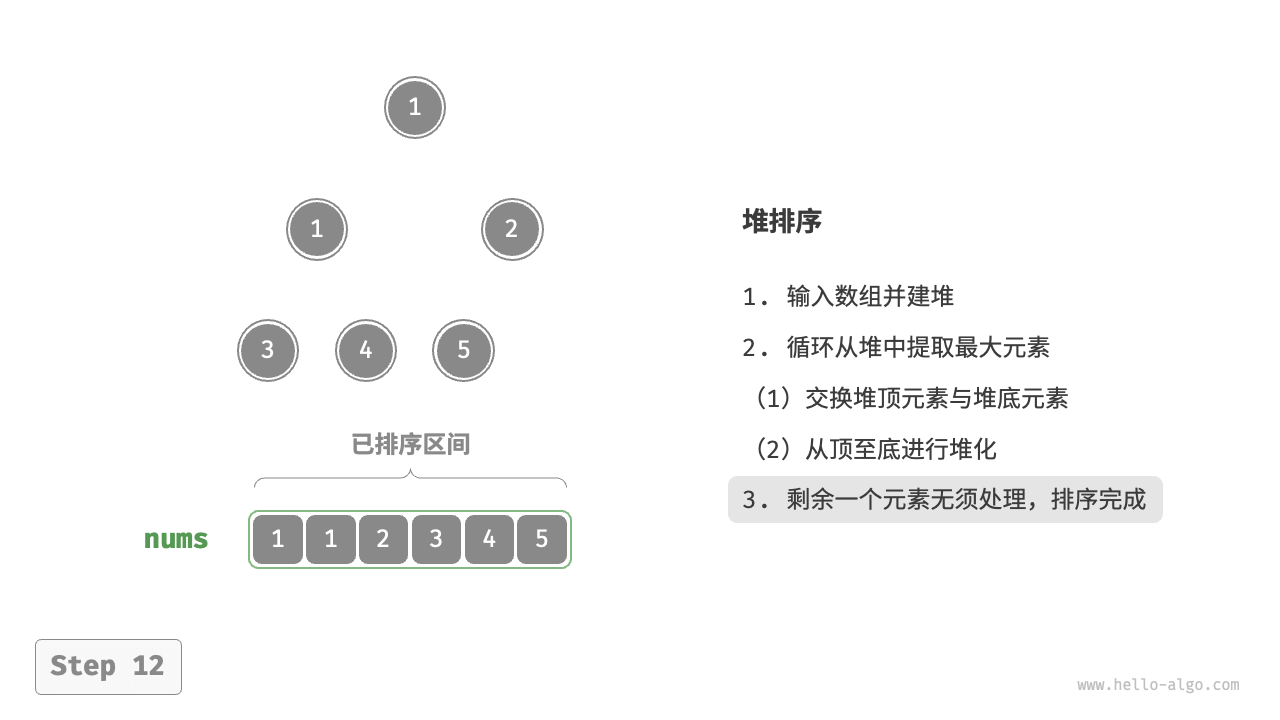
4. 循环执行第 2. 步和第 3. 步。循环 $n - 1$ 轮后，即可完成数组排序。

!!! tip

实际上，元素出堆操作中也包含第 `2.` 步和第 `3.` 步，只是多了一个弹出元素的步骤。

• "<1>"

• "<2>"

• "<3>"

• "<4>"

• "<5>"

• "<6>"

• "<7>"

• "<8>"

• "<9>"

• "<10>"

• "<11>"

• "<12>"

在代码实现中，我们使用了与“堆”章节相同的从顶至底堆化 sift_down() 函数。值得注意的是，由于堆的长度会随着提取最大元素而减小，因此我们需要给 sift_down() 函数添加一个长度参数 $n$ ，用于指定堆的当前有效长度。代码如下所示：

• "Python" ```python def sift_down(nums: list[int], n: int, i: int): """堆的长度为 n ，从节点 i 开始，从顶至底堆化""" while True:

   // 判断节点 i, l, r 中值最大的节点，记为 ma
    l = 2 * i + 1
    r = 2 * i + 2
    ma = i
    if l < n and nums[l] > nums[ma]:
        ma = l
    if r < n and nums[r] > nums[ma]:
        ma = r
   // 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
    if ma == i:
        break
   // 交换两节点
    nums[i], nums[ma] = nums[ma], nums[i]
   // 循环向下堆化
    i = ma
  

def heap_sort(nums: list[int]): """堆排序""" // 建堆操作：堆化除叶节点以外的其他所有节点 for i in range(len(nums) // 2 - 1, -1, -1): sift_down(nums, len(nums), i) // 从堆中提取最大元素，循环 n-1 轮 for i in range(len(nums) - 1, 0, -1): // 交换根节点与最右叶节点（交换首元素与尾元素） nums[0], nums[i] = nums[i], nums[0] // 以根节点为起点，从顶至底进行堆化 sift_down(nums, i, 0)

- "C++"
```cpp
/* 堆的长度为 n ，从节点 i 开始，从顶至底堆化 */
void siftDown(vector<int> &nums, int n, int i) {
    while (true) {
        // 判断节点 i, l, r 中值最大的节点，记为 ma
        int l = 2 * i + 1;
        int r = 2 * i + 2;
        int ma = i;
        if (l < n && nums[l] > nums[ma])
            ma = l;
        if (r < n && nums[r] > nums[ma])
            ma = r;
        // 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
        if (ma == i) {
            break;
        }
        // 交换两节点
        swap(nums[i], nums[ma]);
        // 循环向下堆化
        i = ma;
    }
}

/* 堆排序 */
void heapSort(vector<int> &nums) {
    // 建堆操作：堆化除叶节点以外的其他所有节点
    for (int i = nums.size() / 2 - 1; i >= 0; --i) {
        siftDown(nums, nums.size(), i);
    }
    // 从堆中提取最大元素，循环 n-1 轮
    for (int i = nums.size() - 1; i > 0; --i) {
        // 交换根节点与最右叶节点（交换首元素与尾元素）
        swap(nums[0], nums[i]);
        // 以根节点为起点，从顶至底进行堆化
        siftDown(nums, i, 0);
    }
}

• "Java" ```java / 堆的长度为 n ，从节点 i 开始，从顶至底堆化 / void siftDown(int[] nums, int n, int i) { while (true) {

    // 判断节点 i, l, r 中值最大的节点，记为 ma
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    int ma = i;
    if (l < n && nums[l] > nums[ma])
        ma = l;
    if (r < n && nums[r] > nums[ma])
        ma = r;
    // 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
    if (ma == i)
        break;
    // 交换两节点
    int temp = nums[i];
    nums[i] = nums[ma];
    nums[ma] = temp;
    // 循环向下堆化
    i = ma;
  

  } }

/ 堆排序 / void heapSort(int[] nums) { // 建堆操作：堆化除叶节点以外的其他所有节点 for (int i = nums.length / 2 - 1; i >= 0; i--) { siftDown(nums, nums.length, i); } // 从堆中提取最大元素，循环 n-1 轮 for (int i = nums.length - 1; i > 0; i--) { // 交换根节点与最右叶节点（交换首元素与尾元素） int tmp = nums[0]; nums[0] = nums[i]; nums[i] = tmp; // 以根节点为起点，从顶至底进行堆化 siftDown(nums, i, 0); } } ```

算法特性

• 时间复杂度为 $O(n \log n)$、非自适应排序：建堆操作使用 $O(n)$ 时间。从堆中提取最大元素的时间复杂度为 $O(\log n)$ ，共循环 $n - 1$ 轮。
• 空间复杂度为 $O(1)$、原地排序：几个指针变量使用 $O(1)$ 空间。元素交换和堆化操作都是在原数组上进行的。
• 非稳定排序：在交换堆顶元素和堆底元素时，相等元素的相对位置可能发生变化。