计数排序

「计数排序 counting sort」通过统计元素数量来实现排序，通常应用于整数数组。

简单实现

先来看一个简单的例子。给定一个长度为 $n$ 的数组 nums ，其中的元素都是“非负整数”，计数排序的整体流程如下图所示。

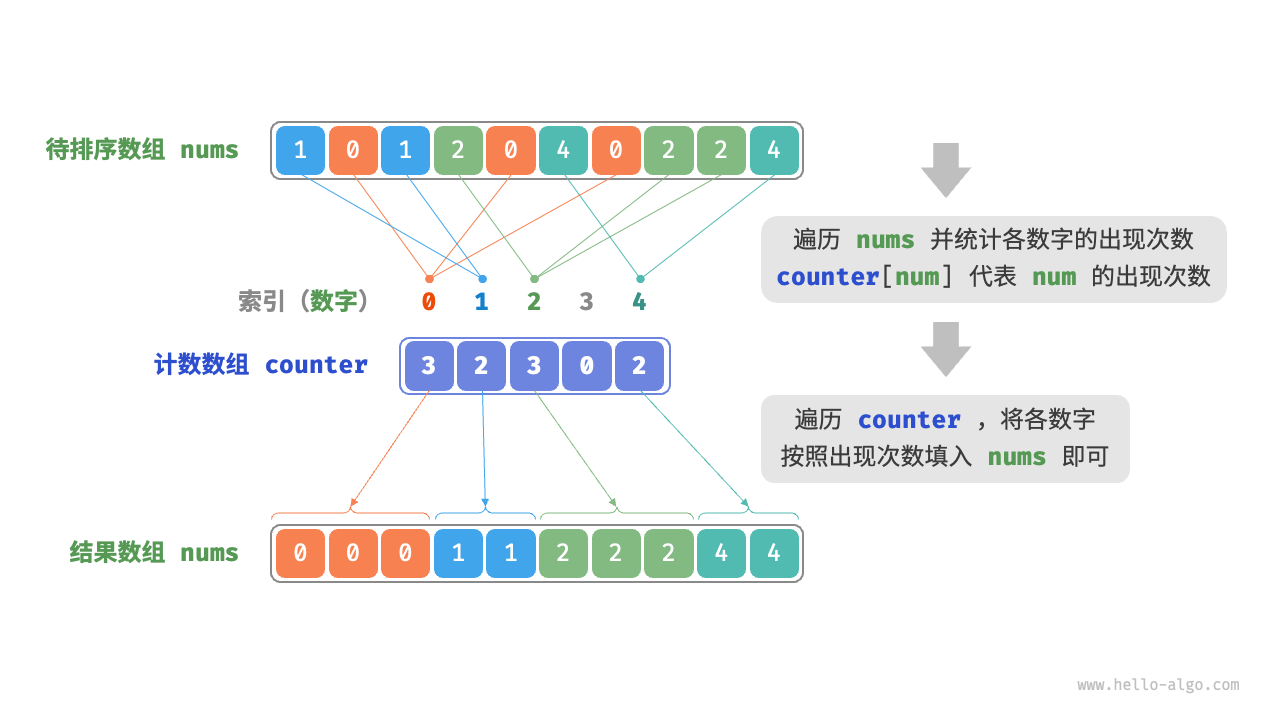
  1. 遍历数组，找出其中的最大数字，记为 $m$ ，然后创建一个长度为 $m + 1$ 的辅助数组 counter 。
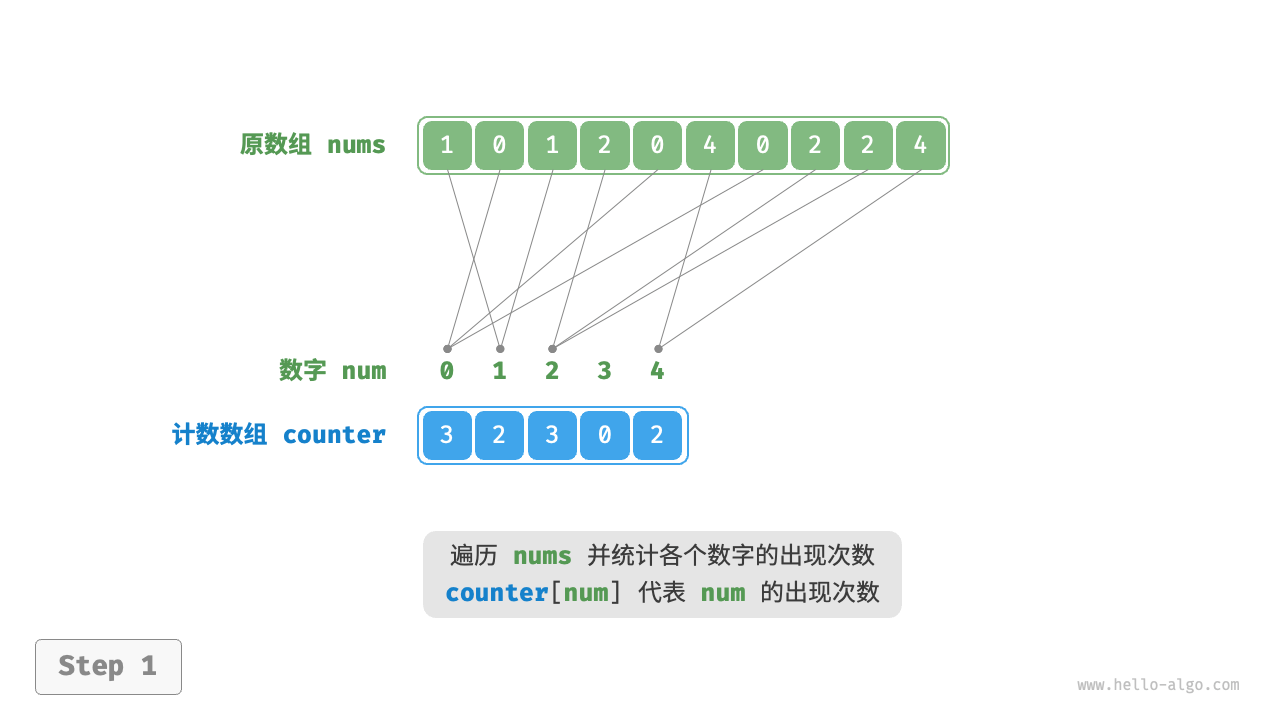
  2. 借助 counter 统计 nums 中各数字的出现次数，其中 counter[num] 对应数字 num 的出现次数。统计方法很简单，只需遍历 nums（设当前数字为 num），每轮将 counter[num] 增加 $1$ 即可。
  3. 由于 counter 的各个索引天然有序，因此相当于所有数字已经排序好了。接下来，我们遍历 counter ，根据各数字出现次数从小到大的顺序填入 nums 即可。

计数排序流程

代码如下所示：

  • "Python"

    def counting_sort_naive(nums: list[int]):
  """计数排序"""
 // 简单实现，无法用于排序对象
 // 1. 统计数组最大元素 m
  m = 0
  for num in nums:
      m = max(m, num)
 // 2. 统计各数字的出现次数
 // counter[num] 代表 num 的出现次数
  counter = [0] * (m + 1)
  for num in nums:
      counter[num] += 1
 // 3. 遍历 counter ，将各元素填入原数组 nums
  i = 0
  for num in range(m + 1):
      for _ in range(counter[num]):
          nums[i] = num
          i += 1

  • "C++"

    /* 计数排序 */
// 简单实现，无法用于排序对象
void countingSortNaive(vector<int> &nums) {
  // 1. 统计数组最大元素 m
  int m = 0;
  for (int num : nums) {
      m = max(m, num);
  }
  // 2. 统计各数字的出现次数
  // counter[num] 代表 num 的出现次数
  vector<int> counter(m + 1, 0);
  for (int num : nums) {
      counter[num]++;
  }
  // 3. 遍历 counter ，将各元素填入原数组 nums
  int i = 0;
  for (int num = 0; num < m + 1; num++) {
      for (int j = 0; j < counter[num]; j++, i++) {
          nums[i] = num;
      }
  }
}

  • "Java"

    /* 计数排序 */
// 简单实现，无法用于排序对象
void countingSortNaive(int[] nums) {
  // 1. 统计数组最大元素 m
  int m = 0;
  for (int num : nums) {
      m = Math.max(m, num);
  }
  // 2. 统计各数字的出现次数
  // counter[num] 代表 num 的出现次数
  int[] counter = new int[m + 1];
  for (int num : nums) {
      counter[num]++;
  }
  // 3. 遍历 counter ，将各元素填入原数组 nums
  int i = 0;
  for (int num = 0; num < m + 1; num++) {
      for (int j = 0; j < counter[num]; j++, i++) {
          nums[i] = num;
      }
  }
}

!!! note "计数排序与桶排序的联系"

从桶排序的角度看，我们可以将计数排序中的计数数组 `counter` 的每个索引视为一个桶，将统计数量的过程看作将各个元素分配到对应的桶中。本质上，计数排序是桶排序在整型数据下的一个特例。

完整实现

细心的读者可能发现了，如果输入数据是对象，上述步骤 3. 就失效了。假设输入数据是商品对象，我们想按照商品价格（类的成员变量）对商品进行排序，而上述算法只能给出价格的排序结果。

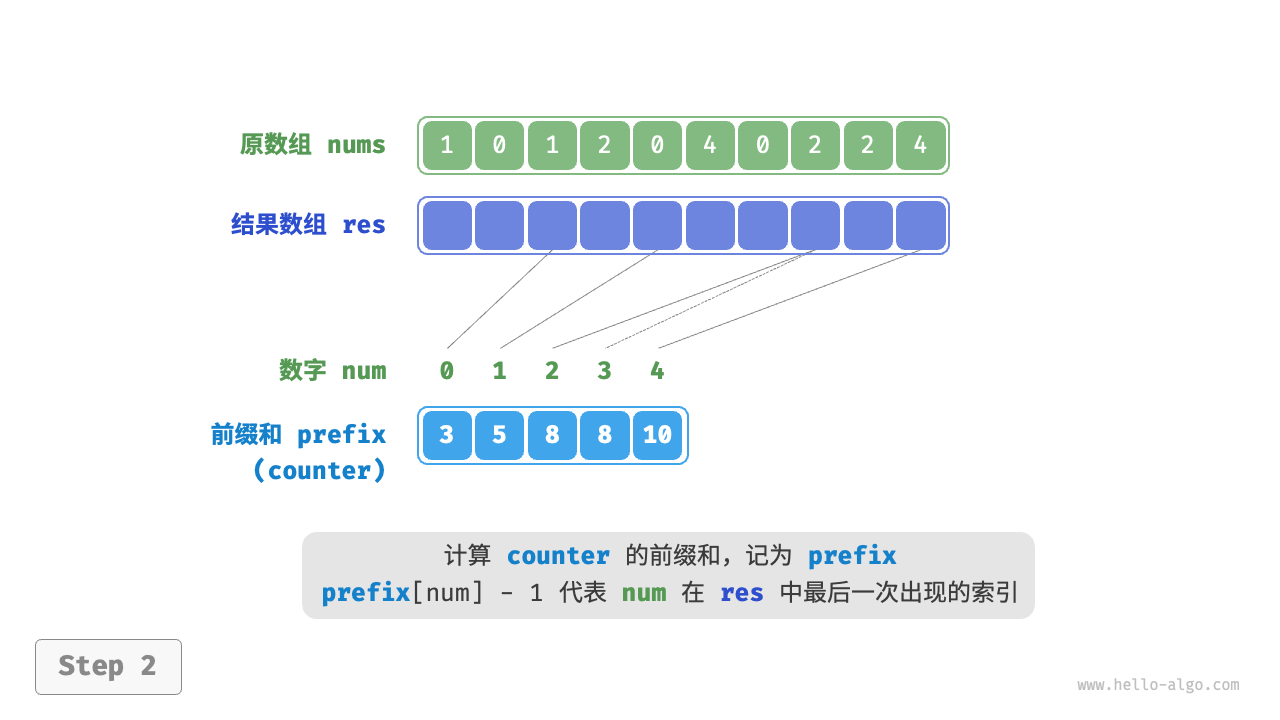
那么如何才能得到原数据的排序结果呢？我们首先计算 counter 的“前缀和”。顾名思义，索引 i 处的前缀和 prefix[i] 等于数组前 i 个元素之和：

$$ \text{prefix}[i] = \sum_{j=0}^i \text{counter[j]}

$$

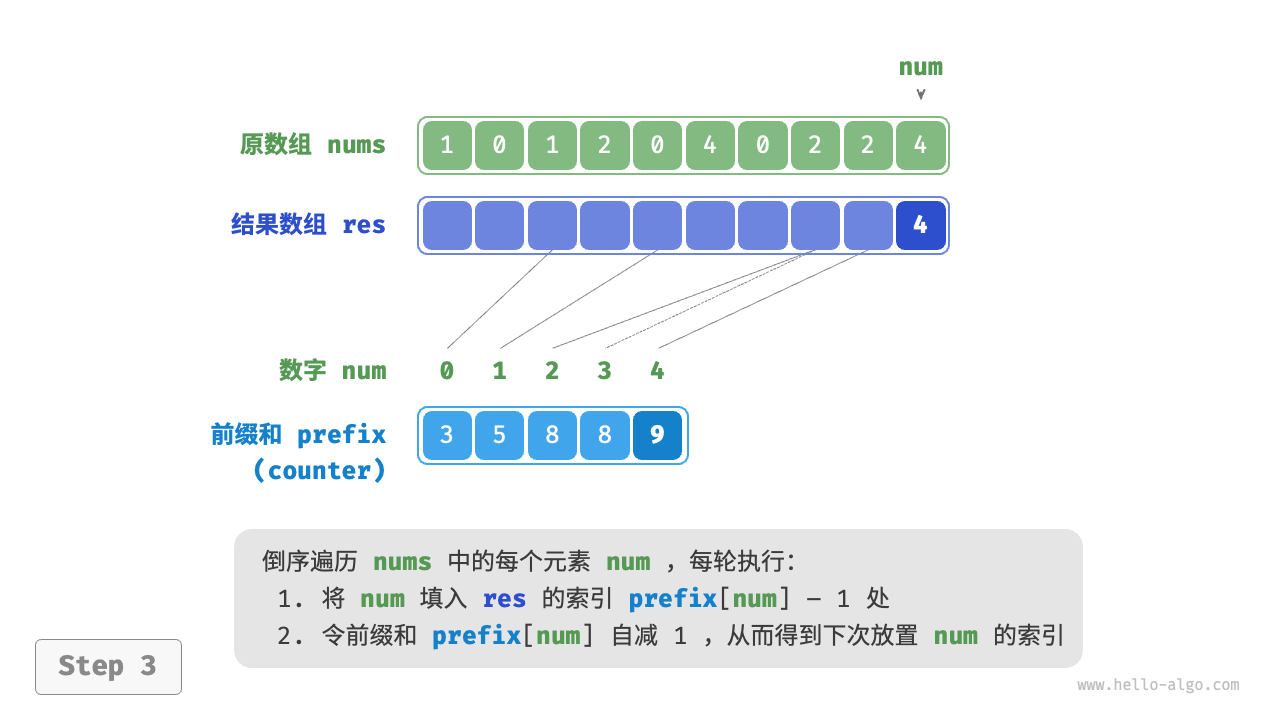
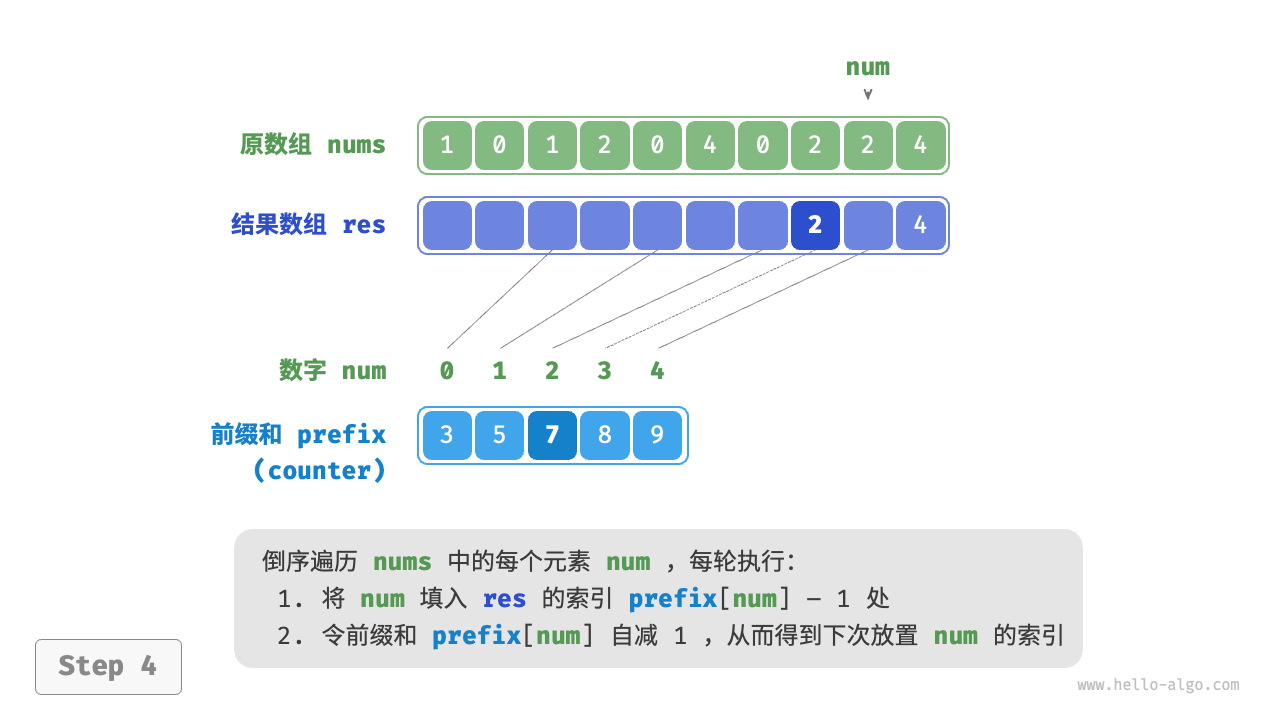
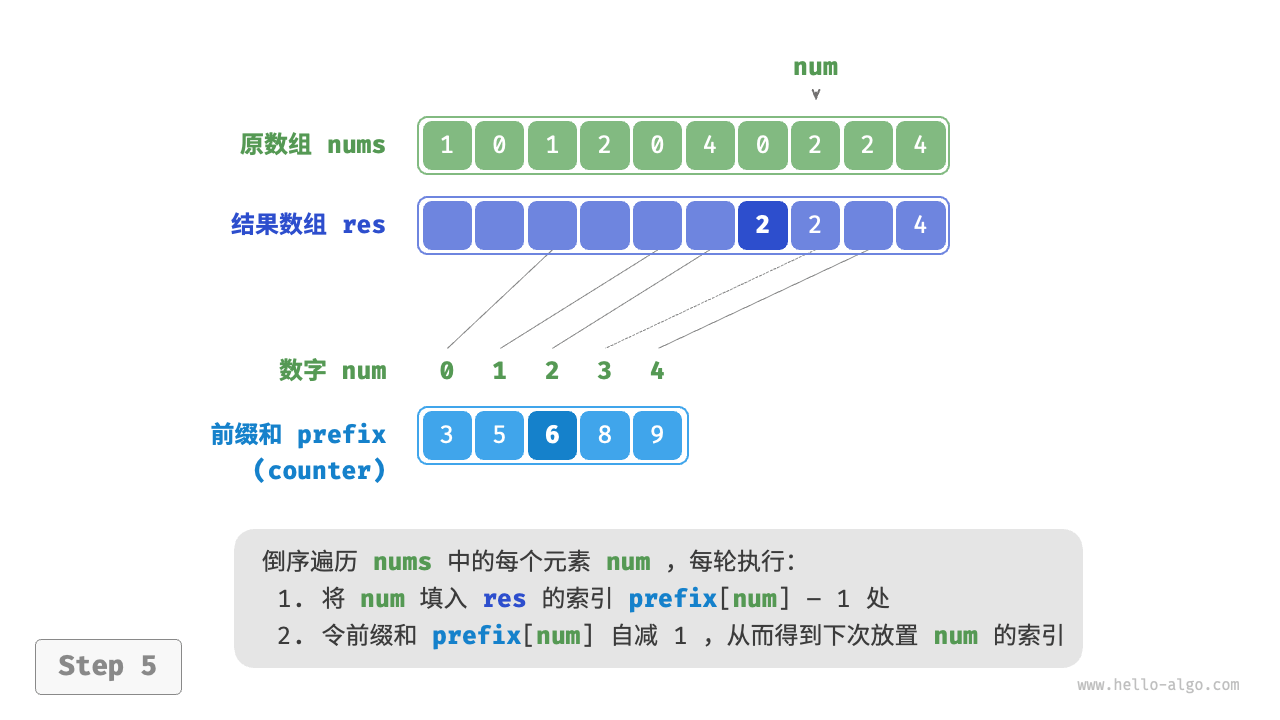
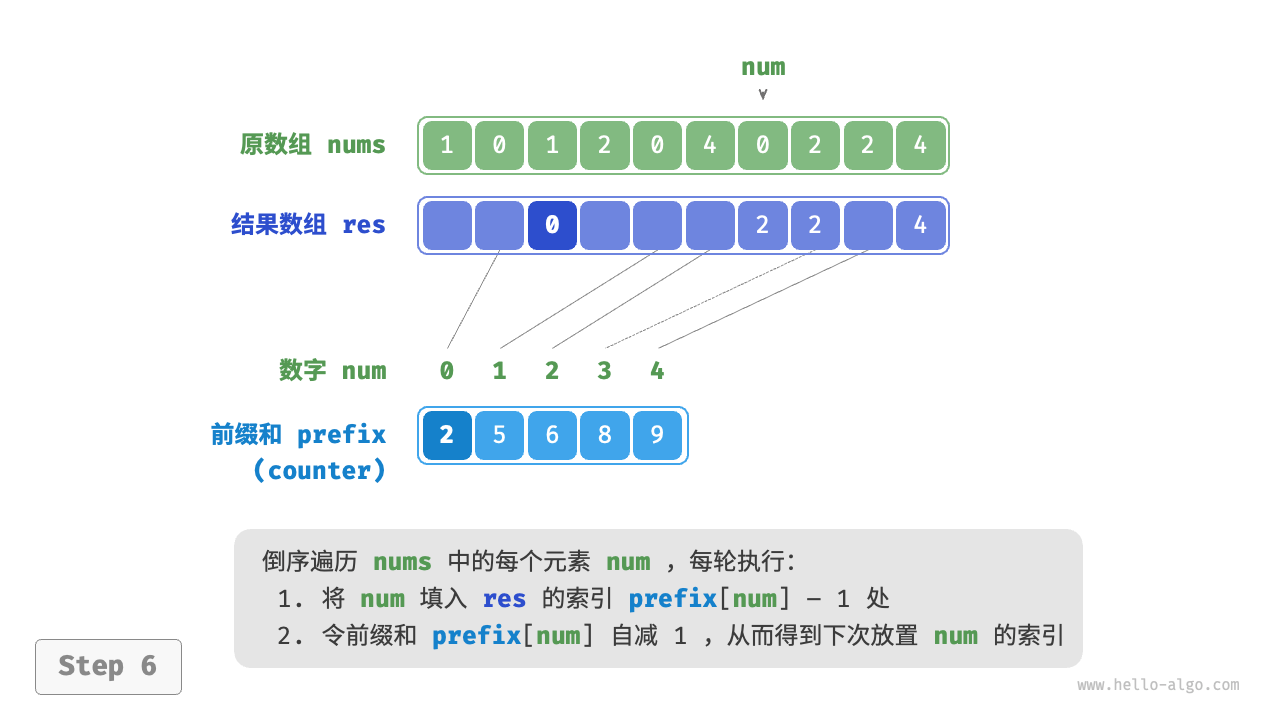
前缀和具有明确的意义，prefix[num] - 1 代表元素 num 在结果数组 res 中最后一次出现的索引。这个信息非常关键，因为它告诉我们各个元素应该出现在结果数组的哪个位置。接下来，我们倒序遍历原数组 nums 的每个元素 num ，在每轮迭代中执行以下两步。

  1. 将 num 填入数组 res 的索引 prefix[num] - 1 处。
  2. 令前缀和 prefix[num] 减小 $1$ ，从而得到下次放置 num 的索引。

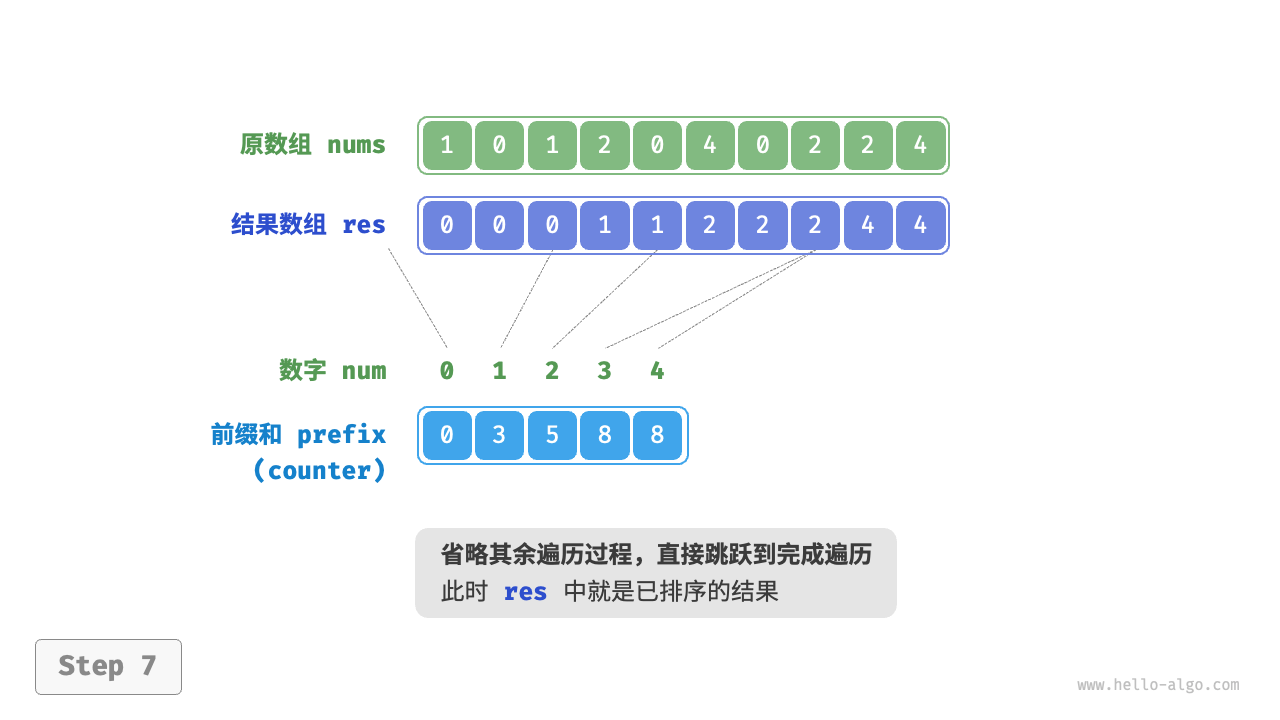
遍历完成后，数组 res 中就是排序好的结果，最后使用 res 覆盖原数组 nums 即可。下图展示了完整的计数排序流程。

  • "<1>" 计数排序步骤

  • "<2>" counting_sort_step2

  • "<3>" counting_sort_step3

  • "<4>" counting_sort_step4

  • "<5>" counting_sort_step5

  • "<6>" counting_sort_step6

  • "<7>" counting_sort_step7

  • "<8>" counting_sort_step8

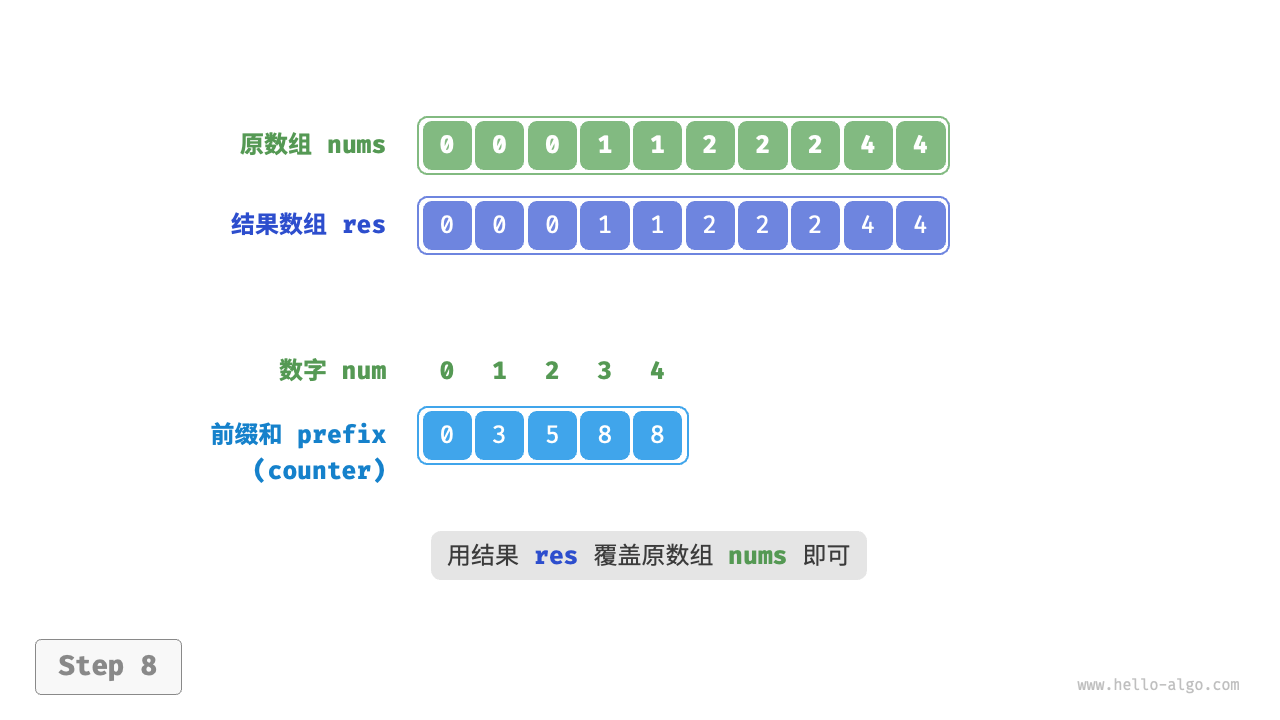
计数排序的实现代码如下所示：

  • "Python"

    def counting_sort(nums: list[int]):
  """计数排序"""
 // 完整实现，可排序对象，并且是稳定排序
 // 1. 统计数组最大元素 m
  m = max(nums)
 // 2. 统计各数字的出现次数
 // counter[num] 代表 num 的出现次数
  counter = [0] * (m + 1)
  for num in nums:
      counter[num] += 1
 // 3. 求 counter 的前缀和，将“出现次数”转换为“尾索引”
 // 即 counter[num]-1 是 num 在 res 中最后一次出现的索引
  for i in range(m):
      counter[i + 1] += counter[i]
 // 4. 倒序遍历 nums ，将各元素填入结果数组 res
 // 初始化数组 res 用于记录结果
  n = len(nums)
  res = [0] * n
  for i in range(n - 1, -1, -1):
      num = nums[i]
      res[counter[num] - 1] = num // 将 num 放置到对应索引处
      counter[num] -= 1 // 令前缀和自减 1 ，得到下次放置 num 的索引
 // 使用结果数组 res 覆盖原数组 nums
  for i in range(n):
      nums[i] = res[i]

  • "C++"

    /* 计数排序 */
// 完整实现，可排序对象，并且是稳定排序
void countingSort(vector<int> &nums) {
  // 1. 统计数组最大元素 m
  int m = 0;
  for (int num : nums) {
      m = max(m, num);
  }
  // 2. 统计各数字的出现次数
  // counter[num] 代表 num 的出现次数
  vector<int> counter(m + 1, 0);
  for (int num : nums) {
      counter[num]++;
  }
  // 3. 求 counter 的前缀和，将“出现次数”转换为“尾索引”
  // 即 counter[num]-1 是 num 在 res 中最后一次出现的索引
  for (int i = 0; i < m; i++) {
      counter[i + 1] += counter[i];
  }
  // 4. 倒序遍历 nums ，将各元素填入结果数组 res
  // 初始化数组 res 用于记录结果
  int n = nums.size();
  vector<int> res(n);
  for (int i = n - 1; i >= 0; i--) {
      int num = nums[i];
      res[counter[num] - 1] = num; // 将 num 放置到对应索引处
      counter[num]--;              // 令前缀和自减 1 ，得到下次放置 num 的索引
  }
  // 使用结果数组 res 覆盖原数组 nums
  nums = res;
}

  • "Java"

    /* 计数排序 */
// 完整实现，可排序对象，并且是稳定排序
void countingSort(int[] nums) {
  // 1. 统计数组最大元素 m
  int m = 0;
  for (int num : nums) {
      m = Math.max(m, num);
  }
  // 2. 统计各数字的出现次数
  // counter[num] 代表 num 的出现次数
  int[] counter = new int[m + 1];
  for (int num : nums) {
      counter[num]++;
  }
  // 3. 求 counter 的前缀和，将“出现次数”转换为“尾索引”
  // 即 counter[num]-1 是 num 在 res 中最后一次出现的索引
  for (int i = 0; i < m; i++) {
      counter[i + 1] += counter[i];
  }
  // 4. 倒序遍历 nums ，将各元素填入结果数组 res
  // 初始化数组 res 用于记录结果
  int n = nums.length;
  int[] res = new int[n];
  for (int i = n - 1; i >= 0; i--) {
      int num = nums[i];
      res[counter[num] - 1] = num; // 将 num 放置到对应索引处
      counter[num]--; // 令前缀和自减 1 ，得到下次放置 num 的索引
  }
  // 使用结果数组 res 覆盖原数组 nums
  for (int i = 0; i < n; i++) {
      nums[i] = res[i];
  }
}

算法特性

  • 时间复杂度为 $O(n + m)$ ：涉及遍历 nums 和遍历 counter ，都使用线性时间。一般情况下 $n \gg m$ ，时间复杂度趋于 $O(n)$ 。
  • 空间复杂度为 $O(n + m)$、非原地排序：借助了长度分别为 $n$ 和 $m$ 的数组 res 和 counter 。
  • 稳定排序：由于向 res 中填充元素的顺序是“从右向左”的，因此倒序遍历 nums 可以避免改变相等元素之间的相对位置，从而实现稳定排序。实际上，正序遍历 nums 也可以得到正确的排序结果，但结果是非稳定的。

局限性

看到这里，你也许会觉得计数排序非常巧妙，仅通过统计数量就可以实现高效的排序。然而，使用计数排序的前置条件相对较为严格。

计数排序只适用于非负整数。若想将其用于其他类型的数据，需要确保这些数据可以转换为非负整数，并且在转换过程中不能改变各个元素之间的相对大小关系。例如，对于包含负数的整数数组，可以先给所有数字加上一个常数，将全部数字转化为正数，排序完成后再转换回去。

计数排序适用于数据量大但数据范围较小的情况。比如，在上述示例中 $m$ 不能太大，否则会占用过多空间。而当 $n \ll m$ 时，计数排序使用 $O(m)$ 时间，可能比 $O(n \log n)$ 的排序算法还要慢。